【ElM分类附matlab代码】基于秃鹰算法优化极限学习机BES-ElM实现数据分类

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机 

内容介绍

随着人工智能和机器学习的迅速发展，数据分类成为了许多领域中的重要任务。数据分类是将一组数据分成不同的类别或标签的过程，它在许多应用中起着至关重要的作用，例如图像识别、语音识别、金融风险评估等。在这个领域中，研究人员一直在寻求更加高效和准确的分类算法。

在过去的几十年中，许多经典的机器学习算法被提出和广泛应用，例如支持向量机(SVM)、人工神经网络(ANN)等。然而，这些算法在处理大规模数据集时存在一些问题，例如计算复杂度高、训练时间长等。为了解决这些问题，研究人员提出了一种新的分类算法，即极限学习机(ELM)。

极限学习机是一种单层前向神经网络，它在训练过程中只需调整输入层和输出层之间的权重，而隐藏层的权重是随机初始化的。这使得ELM具有快速训练和高效的特点。然而，ELM在处理一些复杂的数据集时，仍然存在一些问题，例如分类准确率不高、泛化能力差等。

为了进一步提高ELM的性能，研究人员提出了一种基于秃鹰算法优化的极限学习机(BES-ElM)。秃鹰算法是一种基于自然界中秃鹰捕食行为的优化算法，它模拟了秃鹰在捕食过程中的搜索策略。BES-ElM通过使用秃鹰算法来优化ELM的隐藏层权重，从而提高了ELM的分类性能。

BES-ElM的优化过程包括以下几个步骤：首先，随机初始化隐藏层权重。然后，使用秃鹰算法来搜索最优的隐藏层权重。在搜索过程中，秃鹰算法根据适应度函数评估每个解的质量，并根据一定的策略来更新解的位置。最后，根据优化后的权重进行数据分类。

与传统的ELM相比，BES-ElM具有以下优点：首先，BES-ElM能够更好地适应复杂的数据集，提高了分类准确率。其次，BES-ElM具有更好的泛化能力，能够在未见过的数据上取得较好的分类结果。此外，BES-ElM还具有较快的训练速度和较低的计算复杂度。

然而，虽然BES-ElM在处理数据分类问题上取得了一定的成果，但仍然存在一些挑战和改进的空间。例如，如何选择合适的参数和适应度函数，以及如何处理高维数据集等问题。因此，未来的研究可以进一步探索这些问题，并提出更加高效和准确的优化算法。

总而言之，基于秃鹰算法优化的极限学习机(BES-ElM)是一种有效的数据分类算法。它通过使用秃鹰算法来优化ELM的隐藏层权重，从而提高了ELM的分类性能。虽然BES-ElM仍然需要进一步研究和改进，但它已经显示出了在处理大规模和复杂数据集上的潜力。随着机器学习领域的不断发展，我们相信BES-ElM将在未来得到更广泛的应用和研究。

部分代码

function Y = elmpredict(P,IW,B,LW,TF,TYPE)% ELMPREDICT Simulate a Extreme Learning Machine% Syntax% Y = elmtrain(P,IW,B,LW,TF,TYPE)% Description% Input% P   - Input Matrix of Training Set  (R*Q)% IW  - Input Weight Matrix (N*R)% B   - Bias Matrix  (N*1)% LW  - Layer Weight Matrix (N*S)% TF  - Transfer Function:%       'sig' for Sigmoidal function (default)%       'sin' for Sine function%       'hardlim' for Hardlim function% TYPE - Regression (0,default) or Classification (1)% Output% Y   - Simulate Output Matrix (S*Q)% Example% Regression:% [IW,B,LW,TF,TYPE] = elmtrain(P,T,20,'sig',0)% Y = elmtrain(P,IW,B,LW,TF,TYPE)% Classification% [IW,B,LW,TF,TYPE] = elmtrain(P,T,20,'sig',1)% Y = elmtrain(P,IW,B,LW,TF,TYPE)% See also ELMTRAIN% Yu Lei,11-7-2010% Copyright www.matlabsky.com% $Revision:1.0 $if nargin < 6    error('ELM:Arguments','Not enough input arguments.');end% Calculate the Layer Output Matrix HQ = size(P,2);BiasMatrix = repmat(B,1,Q);tempH = IW * P + BiasMatrix;switch TF    case 'sig'        H = 1 ./ (1 + exp(-tempH));    case 'sin'        H = sin(tempH);    case 'hardlim'        H = hardlim(tempH);end% Calculate the Simulate OutputY = (H' * LW)';if TYPE == 1    temp_Y = zeros(size(Y));    for i = 1:size(Y,2)        [max_Y,index] = max(Y(:,i));        temp_Y(index,i) = 1;    end    Y = vec2ind(temp_Y); end           ​

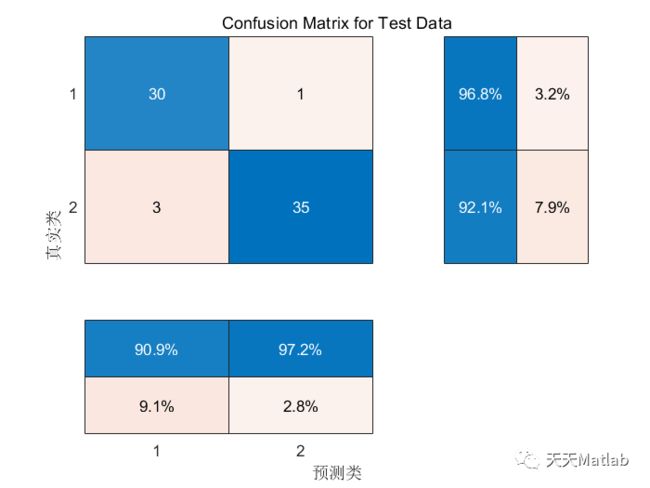
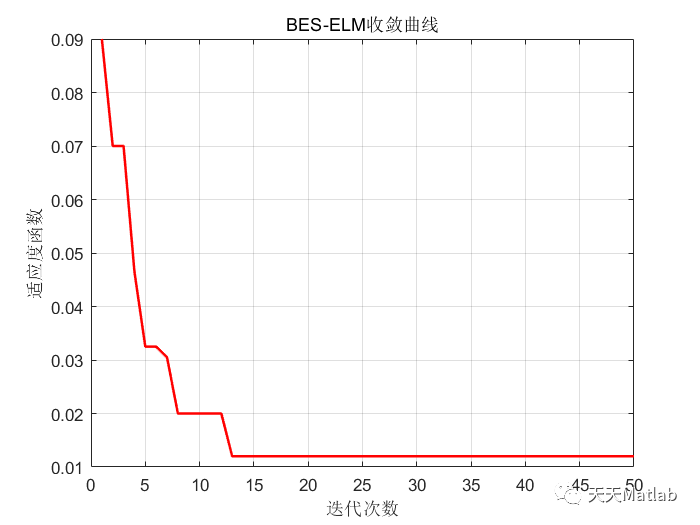
⛳️ 运行结果

参考文献

[1] 刘子诺.基于秃鹰搜索算法和极限学习机的股票价格预测模型[J].中国管理信息化, 2022, 25(22):157-160.

[2] 徐翠.改进极限学习机亚健康识别算法研究[D].辽宁大学,2016.

部分理论引用网络文献，若有侵权联系博主删除

 关注我领取海量matlab电子书和数学建模资料

 私信完整代码和数据获取及论文数模仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合