线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录
1,矩阵定义
2,矩阵的运算
3,方阵的行列式和伴随矩阵
4,矩阵的逆
5,克莱默法则
6,矩阵分块
1,矩阵定义
矩阵与行列式的区别:
(1)形式上行列式是数表加两个竖线,矩阵是数表加大括号或中括号;
(2)行列式可计算得到一个值,矩阵不能;
(3)两个行列式相加与两个矩阵相加不同;
(4)行列式乘以一个数k,可将k乘到行列式任一行或任一列,矩阵乘以k,k与矩阵的每个元素相乘;
(5)行列式是n*n的数表,矩阵可以是m*n的数表;
行数和列数都为n的矩阵称为n阶矩阵,或叫n阶方阵;
只有一行的矩阵称为行矩阵(也叫行向量)在Matlab中的表示方法:
只有一列的矩阵称为列矩阵(也叫列向量)在Matlab中的表示方法:
两个矩阵A、B的行数相同,并且列数也相同时,称它们是同型矩阵,如果他们的对应元素也相同,则A = B;
使用size命令获得矩阵的行数和列数:
clc;
A = [2 4 6;
3 5 7];
size(A)使用isequal判断两个矩阵是否相等:
clc;
A = [2 4 6;
3 5 7];
B = [2 4 6;
3 5 7];
isequal(A,B)单位矩阵:是一个方阵,主队角元素都为1,其他元素是0,一般用E表示
矩阵A乘以单位矩阵E结果还是矩阵A,并且左乘或右乘单位矩阵E一样:
clc;
A = [1 2 3;
4 5 6;
7 8 9];
E = eye(3);
EA = E*A
AE = A*E对角矩阵:是一个方阵,主对角元素不为0,其他元素均为0;
clc;
v = [1,2,3,4];
A = diag(v)2,矩阵的运算
clc;
A = [1 1 1 1;
2 2 2 2;
3 3 3 3];
B = [0 0 0 0;
1 1 1 1;
2 2 2 2];
C = A + Bclc;
A = [1 1 1 1;
2 2 2 2;
3 3 3 3];
k = 2;
C = k*A
 矩阵相乘:一个矩阵的列与另一个矩阵的行相同时,两个矩阵才能相乘;
矩阵相乘:一个矩阵的列与另一个矩阵的行相同时,两个矩阵才能相乘;
clc;
A = [1 1 1;
2 2 2];
B = [1 1;
2 2;
3 3];
C = A*B
D = B*A可见矩阵A*B 不等于B*A;
矩阵的幂:
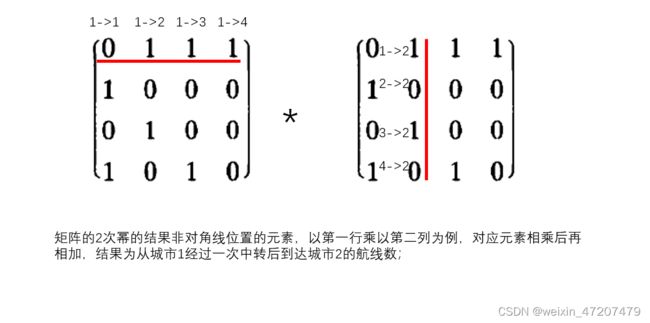
以下例子为四个城市之间开通的航线情况,0代表两个城市间没有航线,1代表开通有航线,建立城市间是否有航线的模型即一个4阶矩阵A,用![]() 表示从i城市到j城市的航线数量,对A求2次幂可以得到城市i有几条双向航线(A的2次幂矩阵的对角线元素),以及从城市i经过一次中转到城市j的单线航线数量。
表示从i城市到j城市的航线数量,对A求2次幂可以得到城市i有几条双向航线(A的2次幂矩阵的对角线元素),以及从城市i经过一次中转到城市j的单线航线数量。
对单线航线矩阵A的2次幂的含义尽心解释:
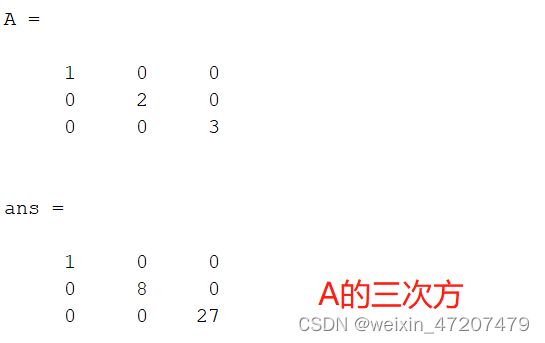
对角矩阵的幂,对角线上元素按幂运算:
clc;
v = [1,2,3];
A = diag(v)
A^3矩阵的转置:
clc;
A = [1 1 1;
2 2 2];
B = A'
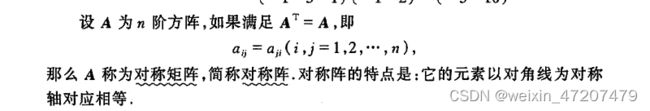 一个方阵和它的转置矩阵相加可以产生一个对称矩阵,以下程序可以产生一个对称阵:
一个方阵和它的转置矩阵相加可以产生一个对称矩阵,以下程序可以产生一个对称阵:
clc;
A = rand(3);
B = A';
C= A+B3,方阵的行列式和伴随矩阵
clc;
A = rand(3);
a = det(A);
b = det(A');
abs(a-b) < epsclc;
A = rand(3);
B = rand(3);
format short
a = det(A*B);
b = det(A)*det(B);
abs(a-b) < epsclc;
A = [1 2 3;
4 5 6;
7 8 9];
k = 2;
B = k*A;
det(B) == (k^3)*det(A)clc;
A = [1 4 7;
3 5 8;
2 6 8];
A_adj = adjoint(A) %adjoint求A的伴随矩阵
C = A*A_adj;
D = A_adj*A;
E = eye(3);
EA = E*det(A);
A13 = A;
A21 = A;
A13(1,:) = [];
A13(:,3) = [];
A21(2,:) = [];
A21(:,1) = [];
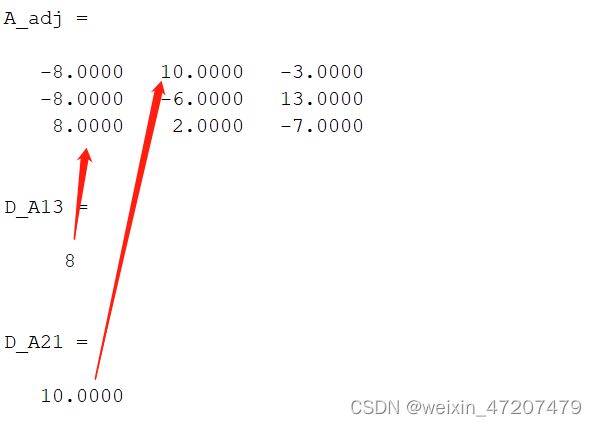
D_A13 = (-1)^(1+3)*det(A13) %A(1,3)的代数余子式
D_A21 = (-1)^(2+1)*det(A21) %A(2,1)的代数余子式使用Matlab中的adjoint命令,A产生的伴随阵A_adj,A*A_adj = A_adj *A = E*det(A):
4,矩阵的逆
只有方阵才有逆矩阵,矩阵可逆的充分必要条件是det(A)不等于0。
Matlab中可以使用inv(A)或A^(-1)计算A的逆矩阵,也可以使用上图中定理2计算逆矩阵:
clc;
A = rand(3);
B = inv(A)
C = A^(-1);
A_mul_B = A*B
B_mul_A = B*A;
A_adj = adjoint(A);
1/det(A)*A_adj %根据定理2计算逆矩阵clc;
A = rand(3);
A_adj = adjoint(A)
det(A)*inv(A) %定理2计算伴随阵5,克莱默法则
分别用逆矩阵、左除、克莱默法则计算下边例题,计算结果相同:
clc;
%以下程序用于求n元非齐次方程组的解, 方程组的形式为Ax = b,求x
A = [1,1,1,1;
1,2,-1,4;
2,-3,-1,-5;
3,1,2,11]; %方程组系数矩阵
b = [5;-2;-2;0]; %方程组右端常数矩阵
A1 = A;
A1(:,1) = b;
A2 = A;
A2(:,2) = b;
A3 = A;
A3(:,3) = b;
A4 = A;
A4(:,4) = b;
if det(A) ~= 0 %判断方程组是否有解
%%三种求方程组解的形式
x = inv(A)*b %1,用逆矩阵的方式求方程组的解
x = A\b %2,用左除的方式求方程组的解
x1 = det(A1)/det(A) %3,用克莱默法则求方程组的解
x2 = det(A2)/det(A)
x3 = det(A3)/det(A)
x4 = det(A4)/det(A)
else
disp("det(A) = 0,方程组无解");
end6,矩阵分块
使用下边Matlab命令运算得到逆矩阵:
clc;
A = [3 0 0 ;
0 2 4 ;
0 3 1 ];
C = mat2cell(A,[1,2],[1,2]); %mat2cell函数将原矩阵分块为四个cell,行数分别为1和2行,列数分别为1列和2列
C1 = C{1}; %将cell转化为矩阵
C2 = C{2};
C3 = C{3};
C4 = C{4};
inv_A = inv(A) %使用inv命令直接计算逆矩阵
inv_C1 = inv(C1); %对分块后的非0矩阵求逆矩阵
inv_C4 = inv(C4);
inv_C = [inv_C1,C3;
C2,inv_C4] %对原矩阵分块后对非0矩阵分别求逆矩阵后再组合在一起运行结果:
矩阵分块后转置:
clc;
A = randi([0,10],3,4) %产生一个3行4列从0-10的随机数元素的矩阵
A_T = A'
C = mat2cell(A,[1,2],[2,2]); %mat2cell函数将原矩阵分块为四个cell,行数分别为1和2行,列数分别为2列和2列
C1 = C{1,1}; %将cell转化为矩阵
C2 = C{1,2};
C3 = C{2,1};
C4 = C{2,2};
C1 = C1';
C2 = C2';
C3 = C3';
C4 = C4';
C_T = [C1,C3;
C2,C4]运行结果:
分块矩阵相乘:
clc;
A = [3 0 0 2 5;
0 2 4 3 4;
0 3 1 2 6];
B = [3 0 0; %矩阵A可以分块为B和C矩阵
0 2 4;
0 3 1];
C = [2 5;
3 4;
2 6];
D = randi([1,10],2,3);
D*A
D*B
D*C运算结果: