蓝桥杯——七段码

问题描述

小蓝要用七段码数码管来表示一种特殊的文字。下图给出了七段码数码管的一个图示。数码管中一共有 7 段可以发光的二极管，分别标记为 a, b, c, d, e, f, g。小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符的表达时，要求所有发光的二极管是连成一片的。
例如：b 发光，其他二极管不发光可以用来表达一种字符。
例如：c 发光，其他二极管不发光可以用来表达一种字符。这种方案与上一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。
例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符

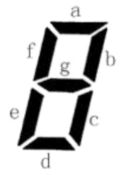
首先，将二极管看成一个点，写出二极管之间的邻接矩阵，如果二极管联通则为1，不连通则为0；

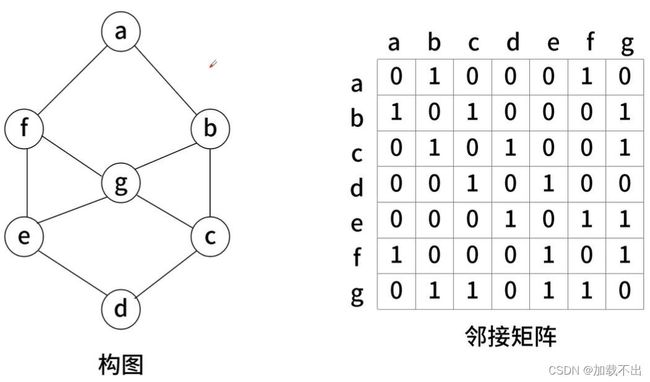
将二极管的状态用0，1表示，0表示二极管不发光，1表示二极管不发光。用choose数组表示7个二极管的状态。比如0000111则表示a,b,c发光，d,e,f,g不发光。7根二极管一共有2^7-1=127种不同的表示方法(去掉全不亮的状态)。
最后用深度优先搜索的方法，将不连通的方法去掉。

#include
using namespace std;
int Edge[7][7]={
  {0,1,0,0,0,1,0},
  {1,0,1,0,0,0,1},
  {0,1,0,1,0,0,1},
  {0,0,1,0,1,0,0},
  {0,0,0,1,0,1,1},
  {1,0,0,0,1,0,1},
  {0,1,1,0,1,1,0}
  };
int choose[7];//对一种方案：若i在该方案中，choose[i]为1,二进制
int visited[7];//DFS过程中，记录顶点是否被访问过的标志
void dfs(int k)
{
  for(int i=0;i<7;i++){
    //i和k相邻，i也包含在该方案中，且i没有访问过
    if(Edge[k][i]&&choose[i]&&!visited[i]){
      visited[i]=1;
      dfs(i);
    }
  }
}
int main()
{
  //ofstream cout("d1.out");
  int i,j,k,x,ans=127;
  for(i=1,i<=127:i++){
    memset(choose,0,sizeof(choose));//清空
    memset(visited,0,sizeof(visited));
    x=i,j=0;
    while(x){//二进制转换
      if(x%2) choose[j]=1;
      x/=2;
      j++;
    }
    k=0;
    while(!choose[k]) k++;//找一个该方案中包含的顶点
    visited[k]=1;
    dfs(k);
    for(j=0;j<7;j++){
      if(choose[j]&&!visited[j]) break;//该方案包含顶点j但没有遍历到
    }
    if(j<7) ans--;
    /*else{//输出方案
        char tmp;
        for(k=0,k<7;k++){
          if(choose[k]){tmp='a'+k;cout<
  }
  cout<<ans<<'\n';
}