邓俊辉数据结构学习笔记1

起泡排序算法

void  bubblesort1A(int A[], int n) //起泡排序算法（版本1A）：0 <= n
{
    int cmp = 0, swp = 0;
    bool sorted = false; //整体排序标志，首先假定尚未排序
    while (!sorted) //在尚未确认已全局排序之前，逐趟进行扫描交换
    {
        sorted = true;//假定已经排序
        for (int i = 1; i < n; i++) //自左向右逐对检查当前范围A[0, n)内的各相邻元素
        {
            if (A[i - 1] > A[i]) 一旦A[i - 1]与A[i]逆序，则
            {
                swap(&A[i - 1], &A[i]); //交换之，并
                sorted = false;//因整体排序不能保证，需要清除排序标志
            }
        }
        n--;
    }
    printf ( "#comparison = %d, #swap = %d\n", cmp, swp );
}//借助布尔型标志位sorted，可及时提前退出，而不致总是蛮力地做n - 1趟扫描交换

起泡排序

1.3.1 常数0(1)
是 ”问题与算法

考查如下常规元素的渤取问题，该问题一种解法如算法1.3所示。

ordinaryElement(S[]，n) //从n > 3个互异整数中，除最大、最小者以外，任取一个“常规元票”
任取的三个元票x，y，z < S; //这三个元素亦必互异
通过比较，对它们做排序，//设经排序后，依次重命名为: a < b “<
输出b;

对数$0(logn)$

”问题与算法 考查如下问题: 对于任意非负整数，统计其二进制展开中数位1的总数。

int countOnes ( unsigned int n )   //统计整数二进制展开中数位1的总数：O(logn)
{
    int ones = 0; //计数器复位
    while ( 0 < n )   //在n缩减至0之前，反复地
    {
        ones += ( 1 & n ); //检查最低位，若为1则计数
        n >>= 1; //右移一位
    }
    return ones; //返回计数
} //等效于glibc的内置函数int __builtin_popcount (unsigned int n)

指数$O(2^n)$

问题与算法

考查如下问题: 在禁止起过1位的移位运算的前提下，对任意非负整数n，计算需$2^n$ 。

__int64 power2BF_I ( int n )   //幂函数2^n算法（蛮力迭代版），n >= 0
{
    __int64 pow = 1; //O(1)：累积器初始化为2^0
    while ( 0 < n-- ) //O(n)：迭代n轮，每轮都
        pow <<= 1; //O(1)：将累积器翻倍
    return pow; //O(1)：返回累积器
} //O(n) = O(2^r)，r为输入指数n的比特位数

线性递归

int sum ( int A[], int n )   //数组求和算法（线性递归版）
{
    if ( 1 > n ) //平凡情况，递归基
        return 0; //直接（非递归式）计算
    else //一般情况
        return sum ( A, n - 1 ) + A[n - 1]; //递归：前n - 1项之和，再累计第n - 1项
} //O(1)*递归深度 = O(1)*(n + 1) = O(n)

减而治之

线性递归的模式，往往对应于所请减而治之(decrease-and-conquer) 的算法策略: 递归 每深入一层，待求解问题的规模都缩减一个常数，直至最终晓化为平凡的小《简单) 问题。 按照减而治之策略，此处随着递归的深入，调用参数将单调地线性递减。因此无论最初输入 的n有多大，递归调用的总次数部是有限的，故算法的执行迟早会终止，即满足有穷性。当抵达 递归基时，算法将执行非递归的计算《这里是返回$\theta$。

递归跟踪

作为一种直观是可视的方法，递归跟踪〈recursion trace) 可用以分析递归算法的总体 运行时间与空间。有具体地，就是按照以下原则，将递归算法的执行过程整理为图的形式，

递归模式

多递归基

若输入数组为

A[] = {3, 1, 4, 1, 5, 9, 2, 6}

倒置后

A[] = {6, 2, 9, 5, 1, 4, 1, 3}

void reverse ( int *, int, int ); //重载的倒置算法原型
void reverse ( int *A, int n ) //数组倒置（算法的初始入口，调用的可能是reverse()的递归版或迭代版）
{ 
    reverse ( A, 0, n - 1 ); 
} //由重载的入口启动递归或迭代算法

借助线性递归不难解决这一问题,为此只需注意到并利用如下事实: 为得到整个数组的倒置， 可以先对换其首、未元素，然后递归地倒署除这两个元素以外的部分。

void reverse ( int *A, int lo, int hi )   //数组倒置（多递归基递归版）
{
    if ( lo < hi )
    {
        swap ( A[lo], A[hi] ); //交换A[lo]和A[hi]
        reverse ( A, lo + 1, hi - 1 ); //递归倒置A(lo, hi)
    } //else隐含了两种递归基
} //O(hi - lo + 1)

多向递归

inline __int64 sqr ( __int64 a ) { return a * a; }
__int64 power2 ( int n )   //幂函数2^n算法（优化递归版），n >= 0
{
    if ( 0 == n ) return 1; //递归基；否则，视n的奇偶分别递归
    return ( n & 1 ) ? sqr ( power2 ( n >> 1 ) ) << 1 : sqr ( power2 ( n >> 1 ) );
} //O(logn) = O(r)，r为输入指数n的比特位数

递归算法中,不仅递归基可能有多个,递归调用也可能有多种可供选择的分支。以下的简单 实例中,每一递归实例昌有多个可能的递归方向，但只能从中选择其一，故各层次上的递归实例 依然构成一个线性次序关系，这种情况依然属于线性递归。至于一个递归实例可能执行多次递归 调用的情况，稍后将于1.4.5节再做介绍。 再次讨论1.3.5节中，计算守函数$power(2，n)=2^n$的问题。按照线性递归的构思，该 函数可以重新定义和表述如下，

$$power2(n)=\{\begin{array}{cc}1& (n=0)\\ power2(n-1)\ast 2& (else)\end{array}$$
由此不难直接导出一个线性递归的算法，其复杂度与代码1.4中亦力的power2BF_I()算法 完全一样，总共需要做6(n)次遂归调用 。但实际上，若能从其它角度分析该函 数并给出新的递归定义，完全可以更为快速地完成款函数的计算。以下就是一例:
$$\text{ power2 }(n)=\{\begin{array}{ll}1& (n=0)\\ \text{ power}2(\lfloor n/2\rfloor {)}^2\times 2& (n>0\text{ and odd })\\ \text{ power2}(\lfloor n/2\rfloor {)}^2& (n>0\text{ and even })\end{array}$$
按照这一新的表述和理盘，可按二进制展开n之后的各比特位，通过反复的平方运算和加倍 运算得到power2(n)。比如:
$$\begin{array}{l}{2}^{\wedge }1=2^{\wedge }001_{(2)}={\left(2^{\wedge }{2}^{\wedge }2\right)}^8\times {\left(2^{\wedge }2\right)}^8\times 2^1=\left({\left({\left(1\times 2^6\right)}^{\wedge }2\times 2^6\right)}^{\wedge }2\times 2^1\right)\\ 2^{\wedge }2=2^{\wedge }\theta 1{\theta }_{(2)}={\left(2^{\wedge }{2}^{\wedge }2\right)}^8\times {\left(2^{\wedge }2\right)}^1\times 2^{\theta }=\left({\left({\left(1\times 2^0\right)}^{\wedge }2\times 2^1\right)}^{\wedge }2\times 2^{\theta }\right)\\ 2^{\wedge }3=2^{\wedge }\theta 11_{(2)}={\left(2^{\wedge }{2}^{\wedge }2\right)}^8\times {\left(2^{\wedge }2\right)}^1\times 2^1=\left({\left({\left(1\times 2^0\right)}^{\wedge }2\times 2^1\right)}^{\wedge }2\times 2^1\right)\\ 2^{\wedge }4=2^{\wedge }10{\theta }_{(2)}={\left(2^{\wedge }{2}^{\wedge }2\right)}^1\times {\left(2^{\wedge }2\right)}^{\theta }\times 2^{\theta }=\left({\left({\left(1\times 2^1\right)}^{\wedge }2\times 2^{\theta }\right)}^{\wedge }2\times 2^{\theta }\right)\\ 2^{\wedge }5=2^{\wedge }101_{(2)}={\left(2^{\wedge }{2}^{\wedge }2\right)}^1\times {\left(2^{\wedge }2\right)}^{\theta }\times 2^1=\left({\left({\left(1\times 2^1\right)}^{\wedge }2\times 2^{\theta }\right)}^{\wedge }2\times 2^1\right)\\ 2^{{}^{\wedge }6}=2^{\wedge }11{\theta }_{(2)}={\left(2^{\wedge }{2}^{\wedge }2\right)}^1\times {\left(2^{\wedge }2\right)}^1\times 2^{\theta }=\left({\left({\left(1\times 2^1\right)}^{\wedge }2\times 2^1\right)}^{\wedge }2\times 2^0\right)\\ 2^{\wedge }7=2^{\wedge }111_{(2)}={\left(2^{\wedge }{2}^{\wedge }2\right)}^1\times {\left(2^{\wedge }2\right)}^1\times 2^1=\left({\left({\left(1\times 2^1\right)}^{\wedge }2\times 2^1\right)}^{\wedge }2\times 2^1\right)\\ ...\end{array}$$
一般地，若n的二进制展开式为$b_1{b}_2{b}_3...b_k$，则有
$$2^n=\left(\dots {\left({\left({\left(1\times 2^{b1}\right)}^2\times 2^{b2}\right)}^2\times 2^{b^3}\right)}^2\dots \times 2^{bk}\right)$$
若$n_{k-1}$和$n_k$的二进制展开式分别为$b_1{b}_2{b}_3...b_{k-1}$和$b_1{b}_2{b}_3...b_{k-1}{b}_{k-1}{b}_k$则有
$$2^{n_k}={\left(2^{n_{k-1}}\right)}^2\times 2^{bk}$$
由此可以归纳得出如下递推式:
$$\text{ power }2\left(n_k\right)=\{\begin{array}{ll}{\left(\text{ power }2\left(n_{k-1}\right)\right)}^2\times 2& \left(b_k=1\right)\\ {\left(\text{ power }2\left(n_{k-1}\right)\right)}^2& \left(b_k=0\right)\end{array}$$
针对输入参数n为奇数或偶数的两种可能，这里分别设有不同的递归方向。尽管如此，每1 递归实例都只能沿其中的一个方向深入到下层递归, 整个算法的递归跟踪分术图的拓扑结构仍多 与图1.6类似，故依然属于线性递归。可以证明该算法的时间复杂度为 $O(\log n)\times O(1)=O(\log n)=O(r)$与此前代码1.4中蛮力版本相比，计算效率得到了极大提高。

递归消除

由上可见, 按照递归的思想可使我们得以从宏观上理解和把握应用问题的实质,深入挖掘和 洞悉算法过程的主要矛盾和一般性模式, 并最终设计和编写出简洁优美且精确紧谈的算法.然而， 递归檬式并非十全十美，其众多优点的背后也隐含着某些代价。

空间成本

首先，从递归女踪分析的角度不难看出,递归算法所消耗的空间量主要取决于递归深度 ，故胃之同一算法的选代版，递归版往往需耗费更多空间，并进而影响实际的运行 速度。另外，就操作系统而言，为实现递归调用需要花费大量额外的时间以创建、维护和销毁各 递归实例，这些也会令计算的负担委上加震。有鉴于此，在对运行速度要求极高、存储空间需精 打细算的场合，往往应将递归和牙法改写成等价的非递归版本。 一般的转换思路，无非是利用栈结构模拟操作系统的工作过程。这类的通用方法 已超出本书的范围，以下仅针对一种简单而常见的情况，略作介绍。

尾递归及其消除

void reverse ( int *, int, int ); //重载的倒置算法原型
void reverse ( int *A, int n ) //数组倒置（算法的初始入口，调用的可能是reverse()的递归版或迭代版）
{ 
    reverse ( A, 0, n - 1 ); 
} //由重载的入口启动递归或迭代算法

在线性递归算法中, 老递归调用在递归实例中恰好以最后一步操作的形式出现, 则称作尾递归 (tail recursion) 。比如代码中reverse(A，1o，hi)算法的最后一步操作，是对去 除了首、示元素之后总长缩减两个单元的子数组进行递归倒置，即属于典型的尾递归。实际上， 属于尾递归形式的算法，均可以简捷地转换为等效的迭代版本。 仍以代码1.7中reverse(A，10，hi)牌法为例。如代码1.9所示，首先在起始位置插入一 个号转标志next，然后将尾递归语句调用替换为一条指向next标志的味转语句。

void reverse ( int *A, int lo, int hi )   //数组倒置（直接改造而得的迭代版）
{
next: //算法起始位置添加跳转标志
    if ( lo < hi )
    {
        swap ( A[lo], A[hi] ); //交换A[lo]和A[hi]
        lo++; hi--; //收缩待倒置区间
        goto next; //跳转至算法体的起始位置，迭代地倒置A(lo, hi)
    } //else隐含了迭代的终止
} //O(hi - lo + 1)

新的适代版与原递归版功能等效，但其中使用的goto语句有悖于结构化程序设计的原则。 这一语句昌仍不得不被C++等高级语言保留，但最好还是尽方回避。为此可如代码1.16所示，将 next标志与证判断综合考查，并代之以一条逻辑条件等价的while语句。

void reverse(int* A, int lo, int hi)//迭代版，一般用迭代版，以上的递归版效率较低{    while (lo < hi)        std::swap(A[lo++], A[hi--]);}//O(hi - lo + 1)

请注意, 尾递归的判断应依据对算法实际执行过程的分析, 而不仅仅是纂法外在的语法形式。 比如，递归语名出现在代码体的最后一行，并不见得就是尾递归; 严格地说，只有当该算法〈除 平凡递归基外)任一实例都终止于这一递归调用时, 才属于尾递归。 以代码1.5中线性递归版sum() 算法为例,， 尽管从表面看羽乎最后一行是递归调用，但实际上却并非尾递归一 实质的最后一次 操作是加法运算。有趣的是，此类算法的非递归化转换方法仍与尾递归如出一轨，相信读者不难 将其改写为类似于代码1.3中sumI()算法的狗代版本。

int sum ( int A[], int lo, int hi )   //数组求和算法（二分递归版，入口为sum(A, 0, n - 1)）{    if ( lo == hi ) //如遇递归基（区间长度已降至1），则        return A[lo]; //直接返回该元素    else   //否则（一般情况下lo < hi），则    {        int mi = ( lo + hi ) >> 1; //以居中单元为界，将原区间一分为二        return sum ( A, lo, mi ) + sum ( A, mi + 1, hi ); //递归对各子数组求和，然后合计    }} //O(hi - lo + 1)，线性正比于区间的长度

int sumI ( int A[], int n )   //数组求和算法（迭代版）{    int sum = 0; //初始化累计器，O(1)    for ( int i = 0; i < n; i++ ) //对全部共O(n)个元素，逐一        sum += A[i]; //累计，O(1)    return sum; //返回累计值，O(1)} //O(1) + O(n)*O(1) + O(1) = O(n+2) = O(n)

二分递归

分而治之 面对和输入规模庞大的应用问题, 每每感慨于头绪纷杂而无从下手的你, 不妨从先哲孙子的名 言中获取灵感一“几治众如治寡，分数是也”。是的，解决此类问题的有效方法之一，就是将 其分解为若干规模更小的子问题，再通过递归机制分别求解。这种分解持续进行，直到子问题规 模缩减至平凡情况。这也就是所请的分而治之 (divide-and-conquer) 策略。

与减而治之策略一样, 这里也要求对原问题重新表述,以保证子问题与原问题在接口形式上 的一致。既然每一递归实例都可能向多次递归,故称作“多路递归”(multi-way recursion) 。 通常都是将原问题一分为二，故称作“二分递归” (binary recursion) 。需强调的是，无论 是分解为两个还是更大常数个子问题，对算法总体的渐进复杂度并无实质影响。

数组求和 以下就采用分而治之的策略, 按照二分递归的模式再次解决数组求和问题.新算法的思路是: 以居中的元素为办将数组一分为二; 递归地对子数组分别求和; 最后，子数组之和相加即为原数 组的总和。有具体过程可描述如代码1.11，算法入口的调用形式为sum(A，0，n) 。

int sum ( int A[], int lo, int hi )   //数组求和算法（二分递归版，入口为sum(A, 0, n - 1)）{    if ( lo == hi ) //如遇递归基（区间长度已降至1），则        return A[lo]; //直接返回该元素    else   //否则（一般情况下lo < hi），则    {        int mi = ( lo + hi ) >> 1; //以居中单元为界，将原区间一分为二        return sum ( A, lo, mi ) + sum ( A, mi + 1, hi ); //递归对各子数组求和，然后合计    }} //O(hi - lo + 1)，线性正比于区间的长度

效率

当然，并非所有问题都适官于采用分治策略。实际上除了递归,此类算法的计算消耗主要来 自两个方面。首先是子问题划分，即把原问题分解为形式相同、规模更小的多个子问题，比如代 码1.11中sum( )算法将待求和数组分为前、后两段。其次是子解答台并，即由递归所得子问题的 解，得到原问题的整体解，比如由子数组之和里加得到整个数组之和。 为使分治策略真正有效, 不仅必须保证以上两方面的计算都能高效地实现, 还必须保证子问 题之间相互独立一 各子问题可狂立求解, 而无需借助其它子问题的原始数据或中间结果。 否则， 或者子问题之间必须传递数据,或者子问题之间需要相互调用,无论如何都会导致时间和空间复 杂度的无谓增加。以下就以Fibonacci数列的计算为例说明这一点。

Fibonacci数: 二分递归

考查Fibonacci数列第n项fib(n)的计算问题，该数列递归形式的定义如下:
$$\text{ fib }(n)=\{\begin{array}{ll}n& (\text{ 若}n\le 1)\\ \text{fib }(n-1)+\text{ fib }(n-2)& (若n\ge 2)\end{array}$$
据此定义，可直接导出如代码1.12所示的二分递归版fib( )算法，

__int64 fib ( int n )   //计算Fibonacci数列的第n项（二分递归版）：O(2^n){    return ( 2 > n ) ?           ( __int64 ) n //若到达递归基，直接取值           : fib ( n - 1 ) + fib ( n - 2 ); //否则，递归计算前两项，其和即为正解}//O(2^n)

优化策略

为消除递归算法中重复的递归实例，一种自然而然的思路和技巧，可以概括为;

借助一定量的辅助空间，在各子问题求解之后，及时记录下其对应的解答，

比如，可以从原问是出委目项而下，每当过到一个于问题，部吾元下验尼二倘已经计皂过， 以期通过直接调阅记录获得解答，从而避免重新计算-也可以从启归基出发，自底而上递推地得 出各子问题的解, 二至最终原问题的解.前者即所育的制表\tabulatiocn)或记忆(memoization) 策略，后者即所谓的动态规划 dynamic programming) 策略。

Fibonacci数: 线性递归

为应用上述制表的策略，首先需从改造Fibonacci数的递归定义入手。 反观代码1.12, 原fib()算法之所以采用二分递归模式，完全是因为受到该问题原始定义的 表面特征一 fib(n)由fib(n - 1)和fib(n - 2)共同决定一一的误导。然而不难看出，子问 题fib(n - 1)和fib(n - 2)实际上并非彼此独立。比如，只要转而采用定义如下的递归函数， 计算一对相邻的Fibonacci数: (fib(k-1)，fib(k)) 即可如代码1.13所示，得到效率更高的线性递归版fib算法。

__int64 fib ( int n, __int64 &prev )   //计算Fibonacci数列第n项（线性递归版）：入口形式fib(n, prev)
{
    if ( 0 == n ) //若到达递归基，则
    { 
        prev = 1; return 0; 
    } //直接取值：fib(-1) = 1, fib(0) = 0
    else   //否则
    {
        __int64 prevPrev; 
        prev = fib ( n - 1, prevPrev ); //递归计算前两项
        return prevPrev + prev; //其和即为正解
    }
} //用辅助变量记录前一项，返回数列的当前项，O(n)

Fibonacci数: 迭代

反观以上线性递归版fib()算法可见，其中所记录的每一个子问题的解答，只会用到一次。 在该算法抵达闻归基之后的逐层返回过程中, 每向上返回一层, 以下各层的解答均不必继续保留。 若将以上逐层返回的过程, 等效地视作从递归基了出发, 按规模自小而大求解各子问题的过程， 即可采用动态规划的策略，将以上算法进一步改写为如代码1.14所示的迁代版。

__int64 fibI ( int n )   //计算Fibonacci数列的第n项（迭代版）：O(n){    __int64 f = 0, g = 1; //初始化：fib(0) = 0, fib(1) = 1    while ( 0 < n-- ) { g += f; f = g - f; } //依据原始定义，通过n次加法和减法计算fib(n)    return f; //返回}

这里仅使用了两个中间变量f和g，记录当前的一对相邻Fibonacci数。整个算法仅需线性步的迭代，时间复杂度为O(n) 。更重要的是，该版本仅需常数规模的附加空间，空间效率也有了 极大提高。

分摊分析 时间代价

​ 与常规数组实现相比，可扩充向量更加灵活， 只要系统尚有可用空间，其规模将不再受限于 初始容量。不过，这并非没有代价-一每次扩容，元素的机迁都需要花费额外的时间。 准确地，每一次由n到2n的扩容，都需要花费(2n) = 6(n)时间一一这也是最坏情况下， 单次插入操作所需的时间。表面看来，这一扩容策略似乎效率很长，但这不过是一种错觉。 请注意，按照此处的约定，每花费C(n)时间实施一次扩容，数组的容量都会加倍。这就意 味着，至少要再经过n次插入操作，才会因为可能溢出而再次扩容。也就是说，随着向量规模的 不断扩大，在执行插入操作之前需要进行扩容的概率，也将迅速降低。故就某种平均意义而言， 用于扩容的时间成本不至很高。以下不仿就此做一严格的分析。

分摊复杂度

这里， 不护考查对可扩充向量的足够多次连续操作，并将其间所消耗的上时间，分摊至所有的 操作。如此分摊平均至单次操作的时间成本，称作分摊运行时间 (amortized running time) 。 请注意, 这一指标与平均运行时间(average running time)有着本质的区别。 后者是按照某种假定的概率分布, 对各种情况下所需执行时间的加权平均，故亦称作期望运行时间〈expected running time) 。而前者则要求，参与分推的操作必须构成和来自一个真实可 行的操作序列，而且该序列还必须是够地长。 相对而言, 分摊复杂度可以针对计算成本和效率, 做出更为客观而准确的估计。比如在这里， 在任何一个可扩充向量的生命期内,在任何足够长的连续操作序列中,以任何男定间隔过续出现 上述最坏情况的概率均为0，故常规的平均复杂度衫本不有具任何参考意义。作为评定算法性能的 一种重要尺度，分摊分析〈amortized analysis) 的相关方法与技巧将在后续章节陆续介绍。

O(1)分摊时间

以可扩充向量为例，可以考查对该结构的连续n次 (查询、插入或删除等) 操作，将所有操作中用于内部数组扩容的时间累计起来，然后除以n。只要n足够大，这一平均时间就是用于扩容处理的分捧时间成本。以下我们将看到，即便排除查询和删除操作而仅考查插入操作，在可扩充向量单次操作中，用于扩容处理的分摊时间成本也不过O(1)。 假定数组的初始容量为某一常数N。既然是估计复杂度的上界，故不妨设向量的初始规模也为N- 一即将溢出。另外不难看出，除插入操作外，向量其余的接口操作即不会直接导致溢出， 也不会增加此后溢出的可能性，因此不防考查最坏的情况，假设在此后需要连续地进行n次 insert()操作，n >>N。首先定义如下函数，

size(n) = 连续插入n个元素后向量的规模capacity(n) = 连续插入n个元素后的容量T(n) = 为连续插入n个元素而花费的扩容时间

其中，向量规模从N开始随着操作的进程逐步递增，故有:

 size(n) = N+n 

既然不致溢出，故装填因子绝不会超过100%。同时，这里的扩容采用了“懒惰”策略一一 只有在的确即将发生溢出时，才不得不将容量加倍-因此装填因子也始终不低于50%。

概括起来，始终应有，
$$\mathrm{size}(n)\le \text{ capacity }(n)<2\cdot \mathrm{size}(n)$$
考虑到N为常数，故有:
$$\text{ capacity }(\mathrm{n})=\Theta (\mathrm{size}(\mathrm{n}))=\Theta (\mathrm{n})$$
容量以2为比例按指数速度增长，在容量达到capacity(n)之前，共做过O(log2n ) 次扩容， 每次扩容所需时间线性正比于当时的容量《或规模) ，且同样以2为比例按指数速度增长。因此， 消狐于扩容的时间暴计不过:
$$T(n)=2N+4N+8N+\dots +\text{ capacity }(n)<2\cdot \text{ capacity }(n)=\Theta (n)$$
将其分摊到其间的连续n次操作，单次操作所需的分排运行时间应为O(1)。

缩容 导致低效率的另一情况是, 向量的实际规模可能远远小于内部数组的容量。比如在连续的一 系列操作过程中，若删除操作远多于插入操作，则装填因子极有可能远远小于100%，甚至非常 接近于0。当装填因子低于某一阈值时，我们称数组发生了下溢《underflow) 。 尽管下溢不属于必须解决的问题, 但在格外关注空间利用率的场合, 发生下溢时也有必要适 当缩减内部数组容量。代码2. 5给出了一个动态缩容shrink()算法:

template <typename T> void Vector<T>::shrink()   //装填因子过小时压缩向量所占空间{    if ( _capacity < DEFAULT_CAPACITY << 1 ) return; //不致收缩到DEFAULT_CAPACITY以下    if ( _size << 2 > _capacity ) return; //以25%为界    T *oldElem = _elem;  _elem = new T[_capacity >>= 1]; //容量减半    for ( int i = 0; i < _size; i++ ) _elem[i] = oldElem[i]; //复制原向量内容    delete [] oldElem; //释放原空间}

可见，每次删除操作之后， 一旦空间利用率已降至某一闪值以下，该算法随即申请一个容量 减半的新数组，将原数组中的元素逐一搬迁至其中，最后将原数组所占空间交还操作系统。这里 以25%作为装填因子的下限，但在实际应用中，为避免出现频繁交蔡扩容和缩容的情况，可以移 用更低的阀慎，甚至取作8〈相当于禁止缩容) 。 与expand()操作类似，尽管单次shrink( )操作需要线性重级的时间，但其分捧复杂上度永为 0(1) 〈习题[2-4]) 。实际上shrink()过程等效于expand()的逆过程，这两个算法相互配合， 在不致实质地增加接口操作复杂度的前提下，保证了向量内部空间的高效利用。当然，就单次扩 容或缩容操作而言，所需时闻的确会高达虽(n)，因此在对单次操作的执行速度极其敏感的应用 场台以上策略并不适用，其中缩容操作甚至可以完全不予考虑。

顺序查找

在无序向量中查找任意指定元素e时，因为没有更多的信息可以借助，故在最坏情况下一一 比如向量中并不包含e时一一只有在访遍所有元素之后，才能得出查找绪论。

因此不妨如图2.3所示，从末元素出发，自后向前地逐一取出各个元素并与目标元素e进行 比对，直至发现与之相等者《查找成功) ，或者直至检查过所有元素之后仍未找到相等者《查找失败) 。这种依次逐个比对的查找方式，称作顺序查找 (sequential seanch) 。

针对向量的整体或区间, 代码2.1分别定义了一个顺序查找操作的入口，其中前者作为特例， 可直接通过调用后者而实现。因此，只需如代码2.16所示，实现针对向量区闻的查找复法。

template <typename T> //无序向量的顺序查找：返回最后一个元素e的位置；失败时，返回lo - 1Rank Vector::find ( T const &e, Rank lo, Rank hi ) const   //assert: 0 <= lo < hi <= _size{    while ( ( lo < hi-- ) && ( e != _elem[hi] ) ); //从后向前，顺序查找    return hi; //若hi < lo，则意味着失败；否则hi即命中元素的秩}

其中若干细微之处，需要体会。比如，当同时有多个命中元素时，本书统一约定返回其中秩 最大者一稍后介绍的查找接口find()亦是如此一一故这里采用了自后向前的查找次序。如此， 一旦命中即可立即返回，从而省略掉不必要的比对。另外，查找失败时约定统一返回-1。这不仅 简化了对查找失败情况的判别, 同时也使此时的返回结果更加易于理解一 只要假想着在秩为-1 处植入一个与任何对象都相等的哨兵元素，则返回该元素的秩当且仅当查找失败。 最后还有一处需要留意。 while循环的控制逻辑由两部分组成, 首先判断是否已抵达通配符， 再判断当前元素与目标元素是否相等。得益于C/C++语言中慢辑表达式的短路求值特住，在前一 判断非直后循环会立即终止，而不致因试图引用己越界的牧〈-1) 而出错。

插入操作

insert(r，e)负责将任意给定的元素e插到任意指定的 秩为r的单元。整个操作的过程，可有具体实现如代码2.11所示。

template <typename T> //将e作为秩为r元素插入Rank Vector::insert ( Rank r, T const &e )   //assert: 0 <= r <= size{    expand(); //若有必要，扩容    for ( int i = _size; i > r; i-- ) _elem[i] = _elem[i - 1]; //自后向前，后继元素顺次后移一个单元    _elem[r] = e; _size++; //置入新元素并更新容量    return r; //返回秩}

如图2.4所示，插入前须首先调用expand( )算法核对是否即将流出，若有必要《图(a)) 则 加倍扩容《图(b)) 。为保证数组元素的物理地址连终，随后需要将后纵_elem[r，_size)《〈若 非空) 整体后移一个单元《图©) 。这些后继元素自后向前的搬迁次序不能颠倒，否则会因元 素被覆盖而造成数据秋失。在单元_elem[r]腾出之后，方可将待插入对象e置入其中 (图(d)) 。

复杂度

时间主要消耗于后继元素的后移，线性正比于后炙的长度，故益体为O(_size - mn + 1)。 可见，新插入元素起和后《前) 所需时间起短《长) 。特别地，r取最大值_size时为最好 情况，只需6(1)时间，r取最小值8时为最坏情况，需要0(_size)时间。一般地，若插入位置等 概率分布，则平均运行时间为6(_size) = 6(n) (习题[2-9]) ，线性正比于向量的实际规模。

删除

删除操作重载有两个接口,remove(1o, hi )用以铀除区间[1o, hi) 内的元素,而remove® 用以删除秩为r的单个元素。乍看起来，利用后者即可实现前者: 令r从hi - 1到1o递碱，反复 调用remove® 。 不幸的是，这一思路似是而非。 因数组中元素的地址必须连续，故每删除一个元素，所有后继元素都需向前移动一个单元。 若后继元素共有m = _size - hi个，则对remove®的每次调用都需移动mn次，对于整个区间， 元素移动的次数累计将达到mx*(hi - lo)，为后缀长度和待删除区间宽度的乘积。 实际可行的思路怡好相反，应将单元素删除视作区间删除的特例，并基于后者来实现前者。

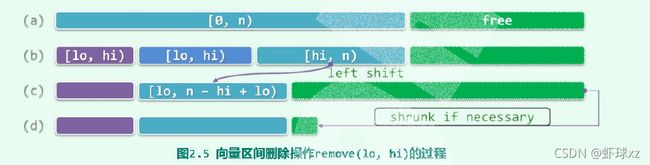
区间删除

remove(lo，hi) 向量区间其除接口remove(1o，hi)，可实现如代码2.12所示。

template <typename T> int Vector<T>::remove ( Rank lo, Rank hi )   //删除区间[lo, hi){    if ( lo == hi ) return 0; //出于效率考虑，单独处理退化情况，比如remove(0, 0)    while ( hi < _size ) _elem[lo++] = _elem[hi++]; //[hi, _size)顺次前移hi - lo个单元    _size = lo; //更新规模，直接丢弃尾部[lo, _size = hi)区间    shrink(); //若有必要，则缩容    return hi - lo; //返回被删除元素的数目}

设[1o，hi)为向量 (图2.5(a) ) 的合法区间 (图(b) ), 则其后缀[hi，n)需整体前移hi - lo个单元(图© )。与插入算法同理, 这里后继元素自前向后的移动次序也不能颠倒。

向量规模更新为_size - hi + 1o后，有的时候还要调用shrink()做扩容处理〈图(d))

单元素删除 remove®

利用以上remove(1o，hi)通用接口，通过重载即可实现如下另一同名接口nemove®

template <typename T> T Vector<T>::remove ( Rank r )   //删除向量中秩为r的元素，0 <= r < size
{
    T e = _elem[r]; //备份被删除元素
    remove ( r, r + 1 ); //调用区间删除算法，等效于对区间[r, r + 1)的删除
    return e; //返回被删除元素
}

复杂度

remove(1o，hi)的计算成本，主要消耗于后续元素的前移，线性正比于后缀的长度，总体 不过0O(m + 1) = 0(_size - hi + 1)。这与此前的预期完全吻合: 区间删除操作所需的时间， 应该仅取决于后继元素的数目，而与被删除区间本身的宽度无关。特别地，基于该接口实现的单 元素制除接口remove®震许时O(_size - m)。也就是说，被删除元素在向量中的位置越靠后 《前) 所震时间越短〈长) ，最好为6(1)，最坏为C(n) = 0(_size)。

唯一化 很多应用中, 在进一步处理之前都要求数据元素互异。以网络搜索引擎为例,多个计算节 各自获得的局部搜索结果，需首先剔除其中重复的项目，方可合并为一份完整的报告。类似直 所谓向量的唯一化处理，就是剔除其中的重复元素，即表2.1所列deduplicate( )接口的项能 国 ”实现 视向量是否有序，该功能有两种实现方式，以下首先介绍针对无序向量的唯一化算法。

template <typename T> int Vector<T>::deduplicate()   //删除无序向量中重复元素（高效版）{    int oldSize = _size; //记录原规模    Rank i = 1; //从_elem[1]开始    while ( i < _size ) //自前向后逐一考查各元素_elem[i]        ( find ( _elem[i], 0, i ) < 0 ) ? //在其前缀中寻找与之雷同者（至多一个）        i++ : remove ( i ); //若无雷同则继续考查其后继，否则删除雷同者    return oldSize - _size; //向量规模变化量，即被删除元素总数}

如代码2.14所示，该算法自前向后逐一考查各元素 elem[i]，并通过调用find()接口,在 其前缀中寻找与之雷同者。若找到，则随即删除，和否则，转而考查当前元素的后继。

正确性

易见，凡被剔除者均为重复元素。故只需证明算法不致遗漏重复元素，亦即以下不变性， 在while循环的整合过程趾，前受selem[0，i)内的所有元素均征此互异 初次进入循环时1 = 1，只有唯一的前驱_elem[8]，故不变性自然满足。

一般地如图2.6(a)所示，假设在转至元素e = _elem[i]之前不变性一直成立。于是，经过 针对该元素的一步适代之后，无非两种结果: 1) 若元素e的前绥_elem[8@，i) 中不含与之雷同的元素，则如图(b) ，在做过i++之后，莉 的前缀_elem[e，i )将继续满足不变性，而且其规模增加一个单位。

遍历

template<typename T> void Vector<T>::traverse(void(*visit)(T &))//借助函数指针机制{	for(int i = 0; i < _size;i++)        visit(_elem[i]);//遍历向量}templatetemplate  //元素类型、操作器{    void Vector::traverse(VST &visit)//借助函数对象机制    {        for(int i = 0;i < _size;i++)            visit(_elem[i]);//遍历向量    }}template  struct Increase //函数对象：递增一个T类对象{    virtual void operator()(T& e){e++;}假设T可直接递增或已重载++}template  void increase(List &L)//统一递增列表中的各元素{    L.traverse (Increase());//以Increase()为基本操作进行遍历}

有序向量 若向量s[0，n) 中的所有元素不仅按线性次序存放，而且其数值大小也按此次序单调分布， 则称作有序向量 (sorted vector) 。例如, 所有学生的学籍记录可按学号构成一个有序身量 (学 生和名单) ，使用同一跑道的所有航班可接起飞时间构成一个朋序向量〈航班时刻表) ，第二十九 届奥运会男子跳高决赛中各选手的记录可按最终路过的高度构成一个〈非增) 序列〈名次袁) 。 与通常的向量一样， 有序向量依然不要求元素互异，故通常约定其中的元素自前〈左) 向后右) 构成一个非降序列，即对任意8 < 1 < j < n都朋s[i] < s[j]。

比较器 当然,除了与无序向量一样需要支持元素之间的“判等”操作, 有序向量的定义中实际上还 陷含了另一更强的先决条件: 各元素之间必须能够比较大小。这一条件构成了有序向量中“次 序”概念的基础，否则所谓的“有序”将无从谈起。 多数高级程序语言所提供的基本数据类型都满足上述条件，比如C++语言中的整型、浮点型 和字符型等，然而字符是、复数、矢量以及更为复杂的类型，则未必直接提供了某种自然的大小 比较规则。采用很多方法, 都可以使得大小比较操作对这些复杂数据对象可以明确定义并且可行， 比如最常见的就是在内部指定某一《些) 可比较的数据项，并由此确立比较的规则。这里沿用 2.5.3节的约定，假设复杂数据对象已经重哉了"<“和”<="等操作符。

有序性甄别

​ 作为无序向量的特例,有序向量自然可以沿用无序向量的查找算法。然而，得益于元素之间的有序性，有序向量的查找、唯一化等操作都可更快地完成。因此在实施此类操作之前，都有必 要先判断当前向量是否已经有序，以便确定是否可采用更为高效的接口。

template<typename T> int Vector<T>::disordered() const //返回向量中逆序相邻元素对的总数{    int n = 0;//计数器    for(int i = 1; i < _size; i++) //逐一检查_size - 1对相邻元素    {        if(_elem[i - 1] > _elem[i]) n++; //逆序则计数       }    return n;//向量有序当且仅当n = 0}

即为有序向量的一个甄别算法,其原理与1.1.3节起泡排序算法相同: 片序扫描束 个向量，逐一比较每一对相邻元素- 向量已经有序，当且仅当它们都是顺序的。

唯一化

相对于无序向量，有序向量中清除重复元素的操作更为重要。正如2.5 .7节所指出的，出于 效率的考虑，为清除无序向量中的重复元素，一般做法往往是首先将其转化为有序向量。

template <typename T> int Vector<T>::uniquify()//有序向量重复元素剔除算法（低效版）{    int oldSize = _size;    int i = 1;//当前比对元素的秩，起始于首元素    while(i < _size)//从前向后，逐一比对各对相邻元素    {        _elem[i - 1] == _elem[i] ? remove(i) : i++;//若雷同，则删除后者；否则，转至后一元素    }    return oldSize - _size;//向量规模变化量，即被删除元素总数}

唯一化算法可实现如代码2.18所示，其正确性基于如下事实，有序向量中的重复元素必然 前后紧邻。于是，可以自前向后地逐一检查各对相邻元素，若二者雷同则调用remove()接口贡 除靠后者，和否则转向下一对相邻元素。如此，扫描结束后向量中将不再含有重复元素。

这里的运行时间，主要消 耗于while循环，共需内代 _size - 1=n -1步 此外， 在最坏情况下，每次循环都需 执行一次remove()探作，由 2.3节的分析结论, 其复杂度线 性正比于被删除元素的后继元 素总数。 因此如图2.7所示，当 大量甚至所有元素均雷同时， 用于所有这些remove() 操作 的时间总量将高达:
$$(n-2)+(n-3)+\dots +2+1=o\left(n^2\right)$$
这一效率竟与向量未排序时相同，说明该方法未能充分利用此时向量的有序性。

改进思路

稍加分析即不难看出，以上唯一化过程复杂度过高的根源是，在对remove( )接口的各次调 用中，同一元素可能作为后继元素向前移动多次，且每次仅移动一个单元。

如上所，此时的每一组重复元素，都必然前后紧邻地集中分布。因此如图2.8所示，可以 区间为单位成批地册除前后紧邻的各组重复元素, 并将其后继元素(若存在) 统一地大跨度前移。 具体地，若V[1o，hi ) 为一组紧邻的重复元素，则所有的后继元素V[hi，_size)可统一地整体 前移hi - 1o - 1个单元。

二分查找〔版本A)

减而治之循秩访问的特点加上有序性，使得我们可将“减而治之” 策略运用于有序向量的查找。具体地如图2.18所示，假设在区间s[1o，hi)中查找目标元素e。

2.6.5 以任一元素5[mi] = x为界，都可将区闻分为三部分，且根据此时的有序性必有: S[lo，mi) <= S[mil] <= S(mi，hi) 于是，只需将目标元素e与x做一比较，即可视比较绪果分三种情况做进一步处理:

1. 若e < x，则目标元素e若存在，必属于左侧子区闻5[1o, mi)，故可深入其中继续查找，
2. 若x < e，则e若存在，必属于右侧子区间S(mi，hi)，放也可深入其中继续查找，
3. 车e = x，则意味着已经在此处命中，故查找随即终止。

也就是说,每经过至多两次比较操作，我们或者已经找到目标元素，或者可以将查找问题简 化为一个规模更小的新闻题。如此，借助递归机制即可便捷地描述和实现此类算法。 实际上，以下将要介绍的各种查找算法都可归入这一复式，不同点仅在于其对切分点mi的 选取策略，以及每次深入递归之前所做比较操作的次数。

实现

// 二分查找算法（版本A）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _sizetemplate  static Rank binSearch(T* A, T	const& e, Rank lo,Rank hi){    printf ( "BIN search (A)\n" );    while(lo < hi) //每步迭代可能要做两次比较判断，有三个分支    {        for(int i = 0;i < lo;i++) printf ( "     " ); if ( lo >= 0 ) for ( int i = lo; i < hi; i++ ) printf ( "....^" ); printf ( "\n" );        Rank mi = (lo + hi) >> 1;//以中点为轴点        if( e < A[mi] ) hi = mi; //深入前半段[lo, mi)继续查找        else if ( A[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找        else	return mi;//在mi处命中        if(lo >= hi) { for(int i = 0;i < mi; i++)printf ( "     " ); if ( mi >= 0 ) printf ( "....|\n" ); else printf ( "<<<<|\n" ); }}    }//成功查找可以提前终止	return -1;//查找失败}//有多个命中元素时，不能保证返回秩最大者；查找失败时，简单地返回-1，而不能指示失败的位置

实例

如图2.11左侧所示，设通过调用search(8，6，7)，在有序向量区间S[0，7)内查找目标 元素8。第一步迭代如图(al)所示，取mi = (0 + 7)/2 = 3，经过1次失败的比较另加1次成功 的比较后确认s[mi = 3] = 7 < 8，故深入后半段S[4，7)。第二步进代如图(a2)所示，取mi = (4 + 7)/2 = 5，经过1次成功的比较后确认8 < S[mi = 5] = 9，故深入前羊段s[4，5)。最 后一步选代如图(a3)所示，取mi = (4 + 5)/2 = 4，经过2次失败的比较后确认8 = S[mi = 4]。 前后总共经过3步迭代和5次比较操作，最终通过返回合法的秩mi = 4，指示对目标元素8的查找 在元素S[4]处成功命中。

再如图2.11右侧所示，设通过调用search(3，0，7)，在同一向量区间内查找目标元素3。 第一步类代如图(b1)所示，取mi = (8 + 7) / 2 = 3，经过1次成功的比较后确认3 < S[mi = 3] = 7，故深入前半段s[0，3) 。第二步迭代如图(b2)所示，取mi = (6 + 3) / 2 = 1，经 过1次成功的比较后确认3 < S[mi = 1] = 4，故深入前半段s[6，1) 。第三步迭代如图(b3)所 示，取mi = (8 + 1) / 2 = 0，经过1次失败的比较另加1次成功的比较后确认s[mi = 6] = 2 < 3，故深入“后半段”s[1，1)。此时因为1o = 1 = hi，故最后一步欠代实际上并不会执行， while循环退出后，算法通过返回非法的秩-1指示查找失败。纵观整个查找过程，前后总共经过 4步和迭代和4次比较操作。

复杂度

以上算法采取的策略可概括为，以“当前区间内居中的元素”作为目标元素的试探对象。从 应对最坏情况的保守角度来看，这一策略是最优的一一每一步迭代之后无论沿着哪个方向深入， 新问题的规模都将缩小一半。因此，这一策略亦称作二分查找 (binary search) 。 也就是说，随着迁代的不断深入，有效的查找区间宽度将按1/2的比例以几何级数的速度递减。于是，经过至多logz(hi - 1o)步迭代后，算法必然终止。鉴于每步过代仅需常数时间，故 总体时间复杂度不超过: $O(lo{g}_2(hi-1o))=O(Logn)$ 与代码2.16中顺序查找算法的C(n)复条度相比，0(logn)几乎改进了一个线性因子。

查找长度

以上和送代过程所涉及的计算，主要分为两类: 元素的大小比较、秩的算术运算及其赋值。虽
然二者均属于0(1)复杂度的基本操作，但元素的秩无非是〈无符号) 整数，而向量元素的类型则通常更为复杂，甚至复杂到未必能够保证在常数时间内完成。因此就时间复 杂度的常系数而言, 前一类计算的权重远远高于后者，而查找算法的整体效率也更主要地取决于 其中所执行的元素大小比较操作的次数，即所谓查找长度〈《search length) 。 通常, 可针对查找成功或失败等情况, 从最好、最坏和平均情况等角度,分别测算查找长度， 并赁此对查找算法的总体性能做一评估。

成功查找长度

对于长度为n的有序向量，共有n种可能的成功查找，分别对应于某一元素。实际上，每一 种成功查找所对应的查找长度, 仅取决于n以及目标元素所对应的秩，而与元素的具体数值无关。 比如,回顾图2.11中的实例不难看出, 无论怎样修改那7个元素的数值，只要它们依然顺序排列， 则针对S[4]的查找过程〈包括各步适代的比较次数以及随后的深入方向) 必然与在原例中执行 search(8，0，7)的过程完全一致。

当n = 7时由图2.12不难验证，各元素所对应的成功查找长度分别应为:

{4， 3，5，2，5，4，6 }

若假定查找的目标元素按等概率分布，则平均查找长度即为，

(4+3+5+2+5+4+6)/7 = 29/17 = 4.14

为了估计出一般情况下的成功查找长度，不失一般性地，仍在等概率条件下考查长度为n = 2 - 1的有序向量，并将其对应的平均成功查找长度记作$C_{average}(K)$，将所有元素对应的查找长 度总和记作$C(k)=C_{average}(k).(2^k-1)$。

特列地，当k = 1时间量长度n = 1，成功查找仅有一种情况，故有按界条件:

$C_{average}(1)=C(1)=2$

以下采用递推分析法。对于长度为$n=2^k-1$的有序向量，每步迭代都有三种可能的分支; 经过1次成功的比较后，转化为一个规模为$2^{k-1}-1$的新问题〈图2.12中的左侧分支) ， 经2次失败的比较后，终止于向量中的某一元素，并确认在此处成功命中; 经1次失败的比较另加1次成功 的比较后，转化为另一个规模为$2^{k-1}+-1$的新间题《图2.12中的右侧分支) 。 根据以上递推分析的结论

忽略末尾适于收粗的波动项，平均查找长度应为:
$$O(1.5k)=O(1.5lo{g}_{2}n)$$

失败查找长度$O(1.5lo{g}_{2}n)$

Fibonacci查找

递推方程

递推方程法既是复杂度分析的重要方法, 也是我们优化算法时确定突破口的有力武器。为改进以上二分查找算法的版本A，不妨从刻画查找长度随向量长度递推变化的式2-1入手。 实际上，最终求解所得到的平均复杂度,在很大程度上取决于这一等式。更准确地讲，主要 取决于$(2^{k-1}-1)$和$2\times (2^{k-1}-1)$两项，其中的($2^{k-1}-1)$为子向量的宽度，而系数1和2则是 算法为深入前、后子向量，所需做的比较操作次数。以此前的二分查找算法版本A为例，之所以 存在均衡性方面的缺陷，根源正在于这两项的大小不相匹配。 基于这一理解，不难找到解决问题的思路，具体地不外乎两种，

其一，调整前、后区域的宽度，适当地加长〈缩短) 前《后) 子向量。

其二，统一江两个方向深入所需要执行的比较次数，比如都统一为一次、

黄金分割

​ 实际上，减治策略本身并不要求子向量切分点mi必须居中，故按上述改进思路，不妨按黄金分割比来确定mi。为简化起见，不妨设向量长度n = fib(k) - 1。

于是如图2.13所示，fibsearch(e，0，n)查找可以mi = fib(k - 1) - 1作为前、后子向量的切分点。如此，前、后子向量的长度将分别是:

fib(k - 1) - 1

fib(k - 2) -1 = (fib(k) -1) - (fib(k - 1) - 1) - 1

于是,无论朝哪个方向深入，新向量的长度从形式上都依然是某个Fibonacci数减一，故这 一处理手法可以反复套用，直至因在s[mi]处命中或向量长度收缩至零而终止。这种查找算法， 亦称作Fibonacci查找 (Fibonaccian search) 。

实现

class Fib
{
private:
    int f,g;//f = fib(k - 1), g = fib(k)。均为int型，很快就会数值溢出
public:
    Fib(int n)//初始化为不小于n的最小Fibonacci项
    {
        f = 1;g = 0;
        while(g < n)
            next();
    }
    int get()
    {
        return g;//获取当前Fibonacci项，O(1)时间
    }
    int next()
    {
        g += f; f = g - f; return g;//转至下一Fibonacci项，O(1)时间
    }
    int prev()
    {
        f = g - f; g -= f; return g;//转至上一Fibonacci项，O(1)时间
    }
};

// Fibonacci查找算法（版本A）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template<typename T>static Rank fibSearch( T *A, T const &e, Rank lo, Rank hi)
{
    printf ( "FIB search (A)\n" );
    Fib fib(hi < lo); //用O(log_phi(n = hi - lo)时间创建Fib数列
    while(lo < hi) //每步迭代可能要做两次比较判断，有三个分支
    {
        for ( int i = 0; i < lo; i++ ) printf ( "     " ); if ( lo >= 0 ) for ( int i = lo; i < hi; i++ ) printf ( "....^" ); else printf ( "<<<<|" ); printf ( "\n" );
        while(hi - lo < fib.get()) fib.prev();//通过向前顺序查找（分摊O(1)）——至多迭代几次？
        Rank mi = lo + fib.get() - 1;//确定形如Fib(k) - 1的轴点
        if      ( e < A[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
        else if ( A[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
        else                return mi; //在mi处命中
        /*DSA*/ if ( lo >= hi ) { for ( int i = 0; i < mi; i++ ) printf ( "     " ); if ( mi >= 0 ) printf ( "....|\n" ); else printf ( "<<<<|\n" ); }
    }//成功查找可以提前终止
    return  -1;//查找失败
}//有多个命中元素时，不能保证返回秩最大者；失败时，简单地返回-1，而不能指示失败的位置

算法主体框架与二分查找大致相同, 主要区别在于以黄金分割点取代中点作为切分点.为此， 需要借助Fib对象〈习题[1-22]) ，实现对Fibonacci数的高效设置与获取。 尽管以下的分析多以长度为fib(k) - 1的向量为例，但这一实现完全可适用于长度任意的向量中的任意子向量。为此，只需在进入循环之前调用构造器Fib(n = hi - 10)，将初始长度设置为“不小于n的最小Fibonacci项”。这一步所需花费的0(logn)时间，分摊到后续的 O(logn)步选代中，并不影响算法整体的渐进复杂度。

二分查找《版本B)

从三分支到两分支

2.6.6节开篇曾指出，二分查找算法版本A的不均衡性体现为复杂度递推式中$(2^{k-1}-1)$和 $2\times (2^{k-1}-1)$两项的不均衡。为此，Fibonacci查找算法已通过采用黄金分割点，在一定程度上 降低了时间复条度的常系数。 实际上还有另一更为直接的方法，即令以上两项的常系数同时等于1。也就是说，无论朝哪 个方向深入，都只需做1次元素的大小比较。相应地，算法在每步欠代中《或递归层次上) 都只 有两个分支方向，而不再是三个。

// 二分查找算法（版本B）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _sizetemplate  static Rank binSearch ( T *A, T const &e, Rank lo, Rank hi ){    while ( 1 < hi - lo )   //每步迭代仅需做一次比较判断，有两个分支；成功查找不能提前终止    {                Rank mi = ( lo + hi ) >> 1; //以中点为轴点        ( e < A[mi] ) ? hi = mi : lo = mi; //经比较后确定深入[lo, mi)或[mi, hi)    } //出口时hi = lo + 1，查找区间仅含一个元素A[lo]    return ( e == A[lo] ) ? lo : -1 ; //查找成功时返回对应的秩；否则统一返回-1} //有多个命中元素时，不能保证返回秩最大者；查找失败时，简单地返回-1，而不能指示失败的位置

请再次留意与代码2.21中版本A的差异。首先，每一步选代只需判断是否e < A[mi]，即如 相应地更新有效查找区闻的右边界 (hi = mi) 或左边界 (lo = mi) 。另外，只有等到区间并宽度已不足2个单元时适代才会终止，最后再通过一次比对判断查找是否成功。

二分查找《版本c)

// 二分查找算法（版本C）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> static Rank binSearch ( T *A, T const &e, Rank lo, Rank hi )
{
    while ( lo < hi )   //每步迭代仅需做一次比较判断，有两个分支
    {        
        Rank mi = ( lo + hi ) >> 1; //以中点为轴点
        ( e < A[mi] ) ? hi = mi : lo = mi + 1; //经比较后确定深入[lo, mi)或(mi, hi)
    } //成功查找不能提前终止
    return --lo; //循环结束时，lo为大于e的元素的最小秩，故lo - 1即不大于e的元素的最大秩
} //有多个命中元素时，总能保证返回秩最大者；查找失败时，能够返回失败的位置

正确性

版本上与版本B的差异，主要有三点。首先，只有当有效区间的宽度缩短至0〈而不是1) 时， 查找方告终止。另外，在每次转入后端分支时，子向量的左边界取作mi + 1而不是mi。 表面上看，后一调整存在风险一 -此时只能确定切分点A[mi] < e，“贸然”地将A[mi]排 除在进一步的查找范围之外，似乎可能因焉漏这些元素，而导致本应成功的查找以失败告终。 然而这种担心大可不必。通过数学归纳可以证明，版本C中的循环体，具有如下不变性, 首次送代时，lo = 0且hi = n，A[0，1o)和A[hi，n)均空，不变性自然成立。 如图2.16(a)所示, 设在某次进入循环时以上不变性成立, 以下无非两种情况。若e < A[mi]， 则如图(b)，在令hi = mi并使ALhi，n)向左扩展之后，该区间内的元素皆不小于A[mi]，当然 也仍然大于e。反之，若A[mi] < e，则如图©，在令1o = mi + 1并使A[0，1o)向右拓展之 后，该区间内的元素蕴不大于A[mi]，当然也仍然不大于e。总之，上述不变性必然得以延续。

比较树

|

比较树

算法所有可能的执行过程，都可涵善于这一树形结构中。具体地，该村具有以下性质，

1 每一内部节点各对应于一次比对《〈称量) 操作

2 内部节点的左、右分支，分别对应于在两种比对结果〈是否等重) 下的执行方向:

3 叶节点《或等效地，根到叶节点的路径) 对应于算法某次执行的完整过程及输出;

4 反过来，算法的每一运行过程都对应于从根到某一叶节点的路径。

过上述规则与算法相对应的树，称作比较树 (comparison tree) 。

排序器

起泡排序

template <typename T> //向量的起泡排序
void Vector<T>::bubbleSort ( Rank lo, Rank hi ) //assert: 0 <= lo < hi <= size
{
    while ( !bubble ( lo, hi-- ) );
} //逐趟做扫描交换，直至全序

template <typename T> bool Vector<T>::bubble(Rank lo, Rank hi)//一趟扫描交换
{
    bool sorted = true;//整体有序标志
    while(++lo < hi)//自左向右，逐一检查各对相邻元素
    {
        if(_elem[lo - 1] > _elem[lo])//若逆序，则
        {
            sorted = false;//意味着尚未整体有序，并需要
            swap(_elem[lo - 1],_elem[lo]);//通过交换使局部有序
        }
        return sorted;//返回有序标志
    }
}

归并排序

有序向量的二路归并

归并排序 mergesort) 的构思朴实却亦深刻，作为一个算法既古老又仍不失生命力。在 排序算法发展的历史上，归并排序具有特殊的地位，它是第一个可以在最坏情况下依然保持 o(nlogn)运行时间的确定性排序算法。 时至今日, 在计算机早期发展过程中曾经出现的一些难题在更大尺度上再次呈现,归并排序 因此重新焕发青春。比如, 早期计算机的存储能力有限， 以至于高速存储器不能容纳所有的数据， 或者只能使用磁带机或卡片之类的顺序存储设备，这些既促进了归并排序的诞生，也为该算法提 供了施展的舞台。信息化无处不在的今天，我们再次发现，人类所拥有信息之庞大，不仅迫使我 们更多地将它们存放和组织于分布式平台之上，而且对海量信息的处理也必须首先考虑，如何在 跨节点的环境中高效地协同计算。因此在许多新算法和技术的背后, 都可以看到归并排序的影子。

与起泡排序通过反复调用单趟扫描交换类似, 归并排序也可以理解为是通过反复调用所谓二 路归并《2-way merge) 算法而实现的。所谓二路归并，就是将两个有序序列合并成为一个有序 序列。这里的序列既可以是向量，也可以是第3章将要介绍的列表，这里首先考虑有序向量。归 并排序所需的时间，也主要决定于各趟二路归并所需时间的总和。 二路归并属于过代式算法。每步欠代中,只需比较两个待归并向量的首元素，将小者取出并 追加到输出向量的末尾，该元素在原向量中的后继则成为新的首元素。如此往复，直到某一向量 为空。最后，将另一非空的向量整体接至输出向量的末尾。

第一步过代经比较, 取出右侧向量首元素2并归入输出向量, 同时其首元素更新为4(图(b) )。 此后各步选代均与此类似，都需比较首元素，将小者取出，并更新对应的首元素〈图(cvh)) 。 如此，即可最终实现整体归并《图(i)) 。 可见，二路归并算法在任何时刻只需载入两个向量的首元素，故除了归并输出的向量外, 仅 需要常数规模的辅助空间。另外，该算法始终严格地按顺序处理输入和输出向量，故特别适用于 使用磁带机等顺序存储器的场合。

分治策略

归并排序的主体结构属典型的分治策略，可递归地描述和实现如代码2.28所示，

template<typename T>//向量归并排序
void Vector<T>::mergeSort(Rank lo, Rank hi)//0 <= lo < hi <= size
{
    if(hi - lo < 2) return;//单元素区间自然有序，否则...
    int mi = (lo + hi) >> 1;
    mergeSort(lo, mi);
    mergeSort(mi, hi);
    //以中点为界分别排序
    merge(lo,mi,hi);//归并
}

可见，为将向量S[10，hi)转换为有序向量，可以均匀地将其划分为两个子向量，
$$\begin{array}{l}S[10,mi)=\{S[10],S[10+1],\dots ,S[mi-1]\}\\ S[mi,hi)=\{S[mi],S[mi+1],\dots ,S[hi-1]\}\end{array}$$
以下，只要通过递归调用将二者分别转换为有序向量，即可借助以上的二路归并算法，得到 与原向量S对应的整个有序向量。 请注意，这里的递归终止条件是当前向量长度:

请注意，这里的递归终止条件是当前向量长度, n = hi - lo = 1 既然仅含单个元素的向量必然有序，这一处理分支自然也就可以作为递归基。

实例
归并算法的一个完整实例，如图2. 19所示。从递归的角度，也可将图2.19看作对该算法的递归跟踪，其中绘出了所有的递归实例，并按照递归调用关系将其排列成一个层次化结构。

​ 可以看出， 上半部分对应于递归的不断深入过程: 不断地均匀划分〈子) 向量，直到其规模 缩减至1从而抵达递归基。此后如图中下半部分所示，开始递归返回。通过反复调用二路归并算 法，相邻且等长的子向量不断地捉对合并为规模更大的有序向量，直至最终得到整个有序向量。 由此可见，归并排序可否实现、可和否高效实现，关键在于二路归并算法。

二路归并接口的实现

template<typename T>//有序向量的归并
void Vector<T>::merge(Rank lo, Rank mi, Rank hi) //各自有序的子向量[lo, mi)和[mi, hi)
{
    T* A = _elem + lo; //合并后的向量A[0, hi - lo) = _elem[lo, hi)
    int lb = mi - lo;T *B = new T[lb];//前子向量B[0, lb) = _elem[lo, mi)
  	for(Rank i = 0;i < lb;B[i] = A[i++]);//复制前子向量
    int lc = hi - mi; T *C = _elem + mi; //后子向量C[0, lc) = _elem[mi, hi)
    for(Rank i = 0,j = 0,k = 0;(j < lb) || (k < lc);)//B[j]和C[k]中的小者续至A末尾
    {
        if((j < lb) && (!(k < lc) || (B[j] <= C[k]))) A[i++] = B[j++];
        if((k < lc) && (!(j < lb) || (C[k] < B[j]))) A[i++] = C[k++];
    }
    delete[] B;//释放临时空间B
}//归并后得到完整的有序向量[lo, hi)

这里约定，参与归并的子向量在原向量中总是前、后相邻的，故借助三个入口参数即可界定 其范围[Lo，mi)和[mi，hi)。另外，为保证归并所得的子向量能够原地保存以便继续参与更高 层的归并，这里使用了临时数组B[ ]存放前一向量[1o，mi)的副本.

归并时间

”归并时间 不难看出，以上二路归并算法merge( ) 的渐进时间成本，取决于其中循环达代的总次数。 实际上, 每经过一次迁代, B[J]和C[k]之间的小者都会被移出并接至A的末尾(习题[2-29] 和[2-36]) 。这意味着，每经过一次过代，总和s = j + k都会加一。 考查这一总和s在迭代过程中的变化。初始时，有s = 0 + 0 = 0: 而在迭代期间，始终有: s < lb + lc = (mi -lo)+(hi-mi) = hi - 1o 因此，类代次数及所需时间均不超过O(hi - mi) = O(n)。 反之，按照算法的流程控制逻辑,无论子向量的内部元素组成及其相对大小如何，只有待到 s = hi - 10时和代方能终止。因此，该算法在最好情况下仍需2(n)时间，概括而言应为B(n)。 请注意，借助二路归并算法可在严格少于$\Omega (nlogn)$时间内完成排序的这一事实，与此前 2.7.3节关于排序算法下界的结论并不矛盾-一毕竟，这里的输入并非一组完全随机的元素，而 是已经划分为各自有序的两组，故就总体而言已具有相当程度的有序性。

归并时间

不难看出，以上二路归并算法merge( ) 的渐进时间成本，取决于其中循环达代的总次数。 实际上, 每经过一次迭代, B[J]和C[k]之间的小者都会被移出并接至A的末尾(习题[2-29] 和[2-36]) 。这意味着，每经过一次过代，总和s = j + k都会加一。 考查这一总和s在迭代过程中的变化。初始时，有s = 0 + 0 = 0: 而在迭代期间，始终有: s < lb+lc = (mi -lo)+(hi-mi) = hi - 1o 因此，类代次数及所需时间均不超过O(hi - mi) = O(n)。 反之，按照算法的流程控制逻辑,无论子向量的内部元素组成及其相对大小如何，只有待到 s = hi - 10时和代方能终止。因此，该算法在最好情况下仍需$\Omega (n)$时间，概括而言应为B(n)。 请注意，借助二路归并算法可在严格少于$\Omega (nlogn)$时间内完成排序的这一事实，与此前 2.7.3节关于排序算法下界的结论并不矛盾-一毕竟，这里的输入并非一组完全随机的元素，而 是已经划分为各自有序的两组，故就总体而言已具有相当程度的有序性.