关于科学选择地图投影类型的探讨
关于科学选择地图投影类型的探讨
作者:左正康(11级GIS 2011221108120027)
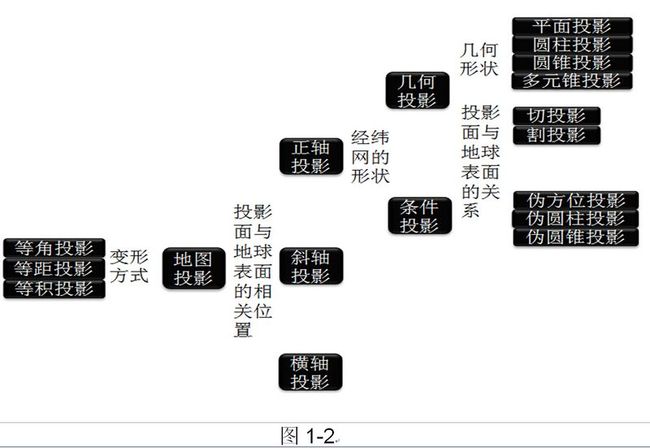
摘要:地图投影是利用一定数学法则把地球表面的经纬线转换到平面上的理论和方法。由于地球是一个赤道略宽两级略扁的不规则的梨形球体,故其表面是一个不可展平的曲面,所以运用任何数学方法进行这种转换都会产生误差和变形,为按照不同的需求缩小误差,就产生了各种投影方法。投影方法按变形方式可以分为等角投影、等积投影、等距投影;按正轴投影时经纬网的形状可以分为几何投影(平面投影、圆锥投影、圆柱投影、多圆锥投影,几何投影中按投影面与地球表面的关系可以分为切投影、割投影)和条件投影(伪方位投影、伪圆柱投影、伪圆锥投影);按投影面与地球表面的相关位置可以分为正轴投影、斜轴投影、横轴投影;本文详细比较了不同投影方法在不同应用中的优缺点,供我们科学的选择地图投影的类型。
关键字:地图投影、分类、优缺点、科学选择
地图投影就是研究将地球椭球体面的经纬线网按照一定的数学法则转移到平面上的方法及其变形问题。分为几何透视法和数学解析法。由于几何透视法难于纠正投影变形,所以往往在透视投影的基础上建立球面与投影面之间点与点的函数关系。正是由于投影变形与人们实际应用的需要之间矛盾的存在,所以我们划定了不同的投影方式,在解读不同的投影方式之前,先解读一下变形椭圆,即地球椭球体面上的一个微小圆,投影到地图平面上后变成的椭圆。模型如图1-1。
图1-2给出了地图投影的不同分类方法,本文以该图为主线,探讨不同投影方式的优缺点以及适用的范围,以供我们做出科学合理的选择。
首先,我们从原理上比较不同的投影方式。
如图1-3,最左边的图是等角投影,其变形椭圆是圆而非椭圆,在小范围内,投影后的图形与实际是相似的;从大范围看,投影后的图形与实际形状并不完全相似。这类投影便于量测方向,故可应用于编制航海图、洋流图、风向图。中间的图是等距投影,可用于对投影变形要求适中或区域较大的地图,如教学地图、科学参考图、世界地图。最右边的图是等积投影,我们可以看出:在此投影的不同点上,变形椭圆的长轴不断拉长,短轴不断缩短,角度变形很大,图形轮廓形状变形很大。此投影无面积变形,可在地图上进行面积对比与量测,故可应用于编制对面积精度要求较高的自然地图和社会经济地图,如地质图、土壤图、行政区划图。
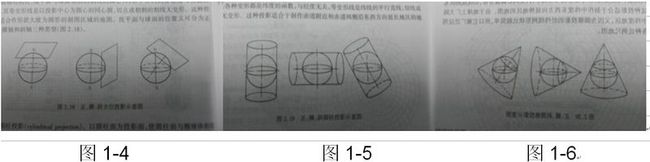
如图1-4为平面投影,以平面为投影面,使平面与椭球体相切或相割,将球面上的经纬线网投影到平面上。此投影的特点是:投影中心(即平面与球面相切的点,或平面与球面相割的割线的中心)向各个方向的方位角与实地相等,切点或相割的割线无变形。可应用于制作形状大致为圆形的制图区域的地图。图1-5为圆柱投影,以圆柱面为投影面,使圆柱面与椭球体相切或相割,将球面上的经纬线网投影到圆柱面上,然后将圆柱面展为平面。可用于制作赤道附近和赤道两侧沿东西方向延长线地区的地图。图1-6为圆锥投影,可用于制作中纬度东西方向延伸地区的地图。
在图1-4,1-5,1-6中,每一幅图根据几何面与球面的关系位置,分为正轴,横轴,斜轴。正轴投影,其纬线为以投影中心为圆心的同心圆,经线为交于投影中心的放射状直线,夹角相等。可用于两级地区和南、北半球图。横轴投影,赤道与中央经线为垂直的直线,其它经纬线为曲线。可用于赤道附近和东、西半球图。斜轴投影,除中央经线为直线外,其余的经纬线均为曲线。可用于其它地区和水、陆半球图。
由于制图时有些特定要求,需要利用数学解析法确定平面与球面之间对应点的函数关系,把球面转化为平面。
图1-7为伪方位投影,在正轴方位投影的基础上,纬线仍为同心圆,除中央经线为直线外,其余的经线均改为对称于中央经线的曲线,且相交于纬线的圆心。可用于编制小比例尺地形图。图1-8为伪圆柱投影,在正轴圆柱投影的基础上,要求纬线仍为平行直线,除中央经线为直线外,其余的经线均改为对称于中央经线的曲线。可用于绘制世界图、大洋图、分洲图。图1-9为伪圆锥投影,在正轴圆锥投影的基础上,要求纬线仍为同心圆,除中央经线为直线外,其余的经线均改为对称于中央经线的曲线。可用于绘制小比例尺的大洲图。图1-10为多圆锥投影,为借助多个圆锥表面与球体相切而设计的投影,纬线为同轴圆弧,其圆心均位于中央经线上,中央经线为直线,其余的经线均为对称于中央经线的曲线。可用于绘制南北方向延伸地区的地图。
接下来,分析一下常见的几种投影。
图2-1为墨卡托投影,正轴等角圆柱投影,经线和纬线是两组相互垂直的平行直线,经线间隔相等,纬线间隔由赤道向两级逐渐扩大。无角度变形,面积变形较大。该投影的等角航线为直线,这一特性对航海有重要意义,可用于编制航海地图,赤道附近国家及一些区域的地图。
图2-2为桑逊投影,经线为正弦曲线的正轴等积伪圆柱投影,纬线为间隔相等的平行直线,经线为对称于中央经线的正弦曲线,赤道和中央经线没有变形,离这两条线越远,长度、角度变形越大。可用于编制世界地图、赤道附近南北延伸地区的地图,如非洲、南美洲地图。
图2-3为摩尔维特投影,经线为椭圆曲线的正轴等积伪圆柱投影,中央经线为直线,离中央经线经差+-90度的经线为一个圆,其余的经线为椭圆曲线。没有面积变形,赤道长度比=0.9,中央经线与南北纬40度44分11.8秒的两个交点没有变形,向外变形逐渐增大。可用于编制世界或大洋图、东西半球地图。
图2-4为古德投影,在摩尔维特投影的基础上,在整个制图区域的几个主要部分,分别设置一条中央经线,然后分别进行投影。从图上可以看出,为了减少投影的变形,图面变的不连续。
图2-5为等差分纬线多圆锥投影,在普通多圆锥投影的基础上设计,赤道与中央经线相互垂直,中央经线长度比=1,其它纬线为凸向并对称于赤道的同轴圆弧,其圆心位于中央经线的延长线上,中央经线上的纬线间隔从赤道向高纬略有放大,其它经线为凹向并对称于中央经线的曲线,其经线间隔随离中央经线距离的增加而按等差级数递减,极点投影成圆弧。该投影能完整地表现太平洋及其沿岸国家,可用于编制各种世界政区图和其它类型的世界地图。
图2-6左图为兰伯特投影,横轴等积方位投影,赤道和中央经线为相互正交的直线,纬线为凸向并对称于赤道的曲线,经线为凹向并对称于中央经线的曲线。可用于编制东、西半球地图。右图为球面投影,横轴等角方位投影,视点在球面,切点在赤道的完全透视的方位投影。
图2-7为博斯特尔投影,正轴等距方位投影,纬线为同心圆,经线为交于圆心的放射状直线,其夹角等于相应的经差。特点:经线方向上没有长度变形,因此纬线间距与实地相等;切点在极点,为无变形点;有角度变形和面积变形,等变形线均以极点为中心,呈同心圆分布,离无变形点愈远,变形愈大。可用于编制南、北半球地图和北极、南极区域地图。
图2-8为斜轴等积方位投影,投影面与椭球面相切于极地与赤道之间的任一点。中央经线上,纬线间距从投影中心向南、北逐渐缩短。可用于编制亚洲、欧洲和北美洲等大区域地图、中国政区图。
图2-9左图为兰伯特正形投影,正轴等角圆锥投影。可用于新编百万分之一地图、全国1:400万、1:600万挂图、全国性普通地图、专题地图。右图为亚尔波斯投影,正轴等积圆锥投影。可用于编制全国性自然地图中的各类分布图、类型图、区划图以及全国性社会经济地图中的行政区划图、人口密度图、土地利用图。
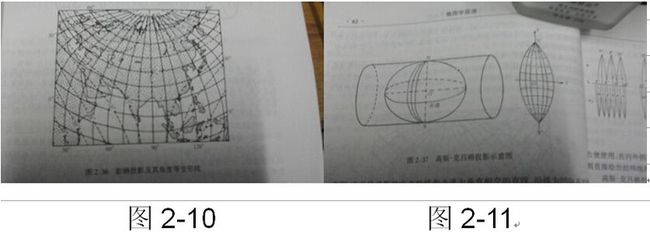
图2-10为彭纳投影,等积伪圆锥投影,中央经线和中央纬线是两条没有变形的线,离这两条线越远,长度,角度变形越大。可用于中纬度地区小比例尺地图,如亚洲政区图、澳大利亚与西南太平洋地图。
图2-11为高斯-克吕格投影,横轴等角切椭圆柱投影,中央经线与赤道垂直,经线为凹向并对称于中央经线的曲线,纬线为凸向并对称于赤道的曲线,经纬线成直角相交,分为6度和3度带分带投影。大于1:1万的地形图采用3度带投影,1:2.5万至1:50万的地形图采用6度带投影。
地图投影的选择是否恰当,直接影响地图的精度和实用价值,因此在编图以前,要根据各种投影的性质、经纬网的形状特点,然后结合制图区域的形状和地理位置、制图区域的范围、地图的内容和用途以及出版方式,科学的选择地图投影。
参考文献:
- 地图学原理(马耀峰,胡文亮,张安定,陈逢珍编著,科学出版社出版)
- 关于地图学中几种投影的选择(豆丁网)
- 地图投影(360百度百科)