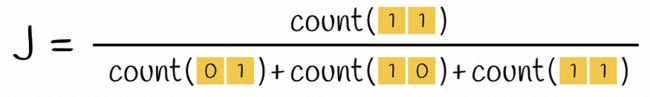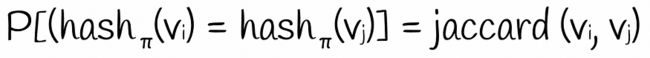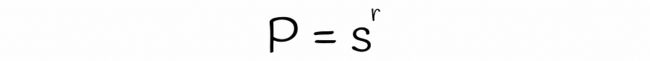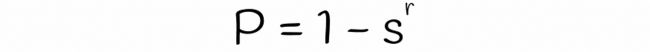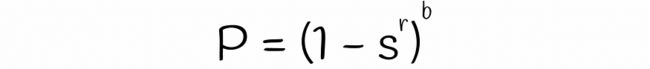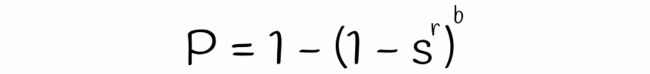相似性搜索：第 5 部分--局部敏感哈希 （LSH）

SImilarity 搜索是一个问题，给定一个查询的目标是在所有数据库文档中找到与其最相似的文档。

一、介绍

        在数据科学中，相似性搜索经常出现在NLP领域，搜索引擎或推荐系统中，其中需要检索最相关的文档或项目以进行查询。在大量数据中，有各种不同的方法可以提高搜索性能。

        在本系列文章的前几部分中，我们讨论了倒排文件索引、产品量化和 HNSW 以及如何将它们一起使用以提高搜索质量。在本章中，我们将研究一种主要不同的方法，该方法可以保持高搜索速度和质量

        本地敏感哈希 （LSH） 是一组方法，用于将数据向量转换为哈希值，同时保留有关其相似性的信息来缩小搜索范围。

我们将讨论由三个步骤组成的传统方法：

1. Shingling：将原始文本编码为矢量。
2. MinHashing：将向量转换为称为签名的特殊表示，可用于比较它们之间的相似性。
3. LSH 函数：将签名块散列到不同的存储桶中。如果一对向量的签名至少落入同一存储桶一次，则它们被视为候选者。

        我们将逐步深入探讨每个步骤在整篇文章中的细节。

二、Shingling

        Shingling是在给定文本上收集k-gram的过程。K-gram 是一组 k 个连续标记。根据上下文，标记可以是单词或符号。带状疱疹的最终目标是使用收集的 k 元语法对每个文档进行编码。我们将为此使用独热编码。但是，也可以应用其他编码方法。

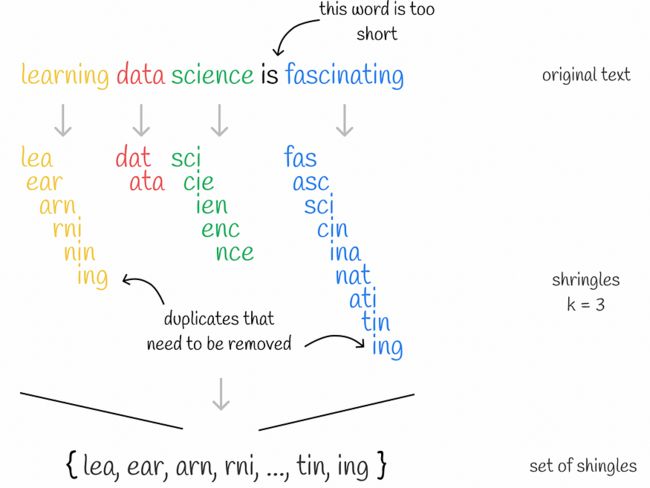
        收集长度 k = 3 的独特小环，用于句子“学习数据科学令人着迷”

        首先，收集每个文档的唯一 k-gram。其次，要对每个文档进行编码，需要一个词汇表，该词汇表表示所有文档中一组唯一的k-gram。然后，为每个文档创建一个长度等于词汇大小的零向量。对于文档中出现的每个 k-gram，都会识别其在词汇表中的位置，并在文档向量的相应位置放置一个“1”。即使相同的 k-gram 在文档中出现多次，也没关系：向量中的值将始终为 1。

独热编码

三、最小哈希

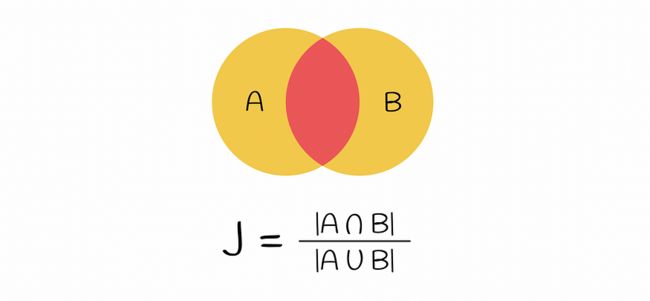
        在此阶段，初始文本已被矢量化。向量的相似性可以通过Jaccard索引进行比较。请记住，两个集合的 Jaccard 索引定义为两个集合中公共元素的数量除以所有元素的长度。

杰卡德指数定义为两个集合并集的交集

        如果采用一对编码向量，则 Jaccard 索引公式中的交集是两个都包含 1 的行数（即 k-gram 出现在两个向量中），并集是至少有一个 1 的行数（k-gram 至少在其中一个向量中呈现）。

        两个向量的杰卡德指数公式

使用上述公式计算两个向量的杰卡德指数的示例

目前的问题是编码向量的稀疏性。计算两个独热编码向量之间的相似性分数将花费大量时间。将它们转换为密集格式将使以后对它们进行操作更有效。最终，目标是设计这样一个函数，将这些向量转换为更小的维度，保留有关其相似性的信息。构造此类函数的方法称为 MinHashing。

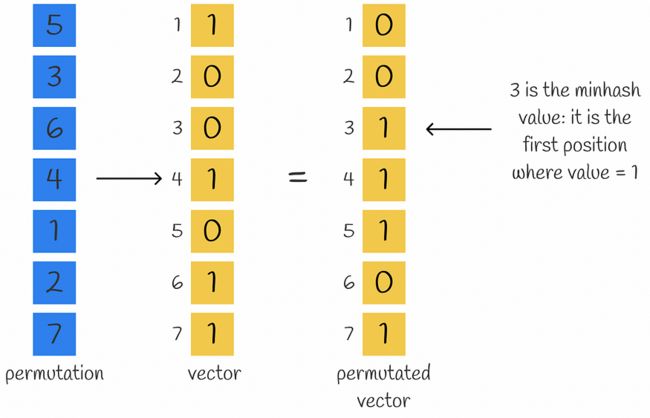
最小哈希是一个哈希函数，它排列输入向量的分量，然后返回置换向量分量等于 1 的第一个索引。

计算给定向量和排列的最小哈希值的示例

为了获得由 n 个数字组成的向量的密集表示，可以使用 n minhash 函数来获取形成签名的 n 个最小哈希值。

乍一听可能并不明显，但可以使用几个 minhash 值来近似向量之间的 Jaccard 相似性。事实上，使用的最小哈希值越多，近似值就越准确。

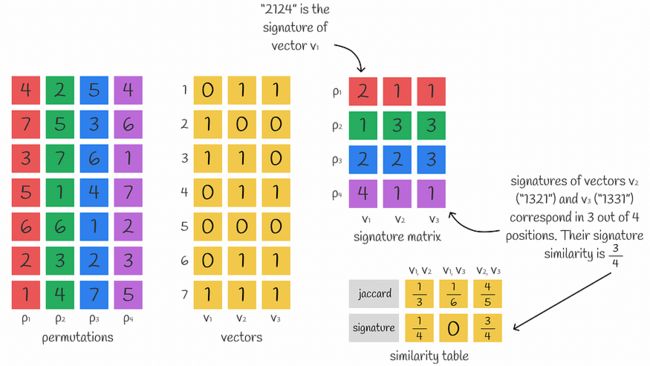
特征矩阵的计算以及如何使用它来计算向量之间的相似性。使用 Jaccard 相似性和签名计算的相似性通常应大致相等。

这只是一个有用的观察。事实证明，幕后有一个完整的定理。让我们了解为什么可以使用签名来计算Jaccard指数。

3.1 声明证明

        假设给定的向量对仅包含类型 01、10 和 11 的行。然后对这些向量执行随机排列。由于所有行中至少存在一个 1，因此在计算两个哈希值时，这两个哈希值计算过程中的至少一个将在相应哈希值等于 1 的向量的第一行停止。

        第二个哈希值等于第一个哈希值的概率是多少？显然，仅当第二个哈希值也等于 1 时，才会发生这种情况。这意味着第一行必须是类型 11。由于排列是随机进行的，因此此类事件的概率等于 P = count（11） / （count（01） + count（10） + count（11））。此表达式与 Jaccard 索引公式完全相同。因此：

基于随机行排列获得两个二进制向量相等哈希值的概率等于 Jaccard 索引。

        但是，通过证明上述陈述，我们假设初始向量不包含类型 00 的行。很明显，类型 00 的行不会更改 Jaccard 索引的值。同样，获得包含类型为 00 的行的相同哈希值的概率也不会影响它。例如，如果第一个排列行是 00，则 minhash 算法会忽略它并切换到下一行，直到一行中至少存在一个 1。当然，类型 00 的行可以产生与没有它们不同的哈希值，但获得相同哈希值的概率保持不变。

        我们已经证明了一个重要的声明。但是如何估计获得相同最小哈希值的概率呢？当然，可以为向量生成所有可能的排列，然后计算所有最小哈希值以找到所需的概率。出于显而易见的原因，这是无效的，因为大小为 n 的向量的可能排列数等于 n！。尽管如此，概率可以近似地评估：让我们只使用许多哈希函数来生成那么多哈希值。

两个二进制向量的 Jaccard 索引大约等于其签名中相应值的数量。

数学符号

很容易注意到，采用更长的签名会导致更准确的计算。

四、LSH功能

        目前，我们可以将原始文本转换为等长的密集签名，保留有关相似性的信息。然而，在实践中，这种密集的签名通常仍然具有很高的维度，直接比较它们是低效的。

        考虑 n = 10⁶ 个文档，其签名长度为 100。假设单个签名需要 4 个字节来存储，那么整个签名将需要 400 个字节。为了存储 n = 10⁶ 文档，需要 400 MB 的空间，这在现实中是可行的。但是以蛮力方式将每个文档相互比较需要大约 5 * 10¹¹ 的比较，这太多了，尤其是当 n 更大时。

        为了避免这个问题，可以构建一个哈希表来加速搜索性能，但即使两个签名非常相似并且仅在 1 个位置上不同，它们仍然可能具有不同的哈希值（因为向量余数可能不同）。但是，我们通常希望它们落入同一个桶中。这就是利星行的救援之用。

LSH 机制构建一个由多个部分组成的哈希表，如果它们至少有一个对应的部分，则将其放入同一存储桶中。

        LSH 采用一个特征矩阵，并将其水平划分为相等的 b 部分，称为带，每个部分包含 r 行。不是将整个签名插入单个哈希函数中，而是将签名除以 b 部分，每个子签名由哈希函数独立处理。因此，每个子签名都属于单独的存储桶。

        使用 LSH 的示例。长度为 9 的两个签名分为 b = 3 个波段，每个波段包含 r = 3 行。每个子向量都散列到 k 个可能的存储桶之一中。由于在第二波段中存在匹配（两个子向量具有相同的哈希值），因此我们认为一对这些签名作为候选者是最近的邻居。

        如果两个不同签名的相应子向量之间至少存在一次冲突，则这些签名被视为候选签名。正如我们所看到的，这个条件更灵活，因为将向量视为候选者，它们不需要绝对相等。然而，这增加了误报的数量：一对不同的签名可以有一个对应的部分，但总体上是完全不同的。根据问题的不同，优化参数 b、r 和 k 总是更好。

五、错误率

        使用 LSH，可以估计两个具有相似 s 的签名在给定每个波段数 b 和行数 r 的情况下被视为候选者的概率。让我们分几个步骤找到它的公式。

        两个签名的一个随机行相等的概率

        一个具有 r 行的随机波段相等的概率

        一个具有 r 行的随机波段不同的概率

        表中所有 b 波段不同的概率

        b 波段中至少有一个相等的概率，因此两个签名是候选的

        请注意，当不同的子向量意外散列到同一个存储桶中时，该公式不考虑冲突。正因为如此，签名成为候选人的真实概率可能差别不大。

5.1 例

        为了更好地理解我们刚刚获得的公式，让我们考虑一个简单的例子。考虑两个长度为 35 个符号的签名，它们平均分为 5 个波段，每个波段 7 行。下表表示基于Jaccard相似性至少有一个相等带的概率：

根据两个签名的相似性获得至少一个对应带的概率 P

        我们注意到，如果两个相似的签名具有 80% 的 Jaccard 相似性，那么它们在 93.8% 的情况下具有相应的条带（真阳性）。在其余6.2%的情况下，这样的一对签名是假阴性的。

        现在让我们采用两个不同的签名。例如，它们仅相似 20%。因此，在 0.224% 的情况下，它们是误报候选者。在其他 99.776% 的情况下，它们没有类似的波段，因此它们是真阴性。

5.2 可视 化

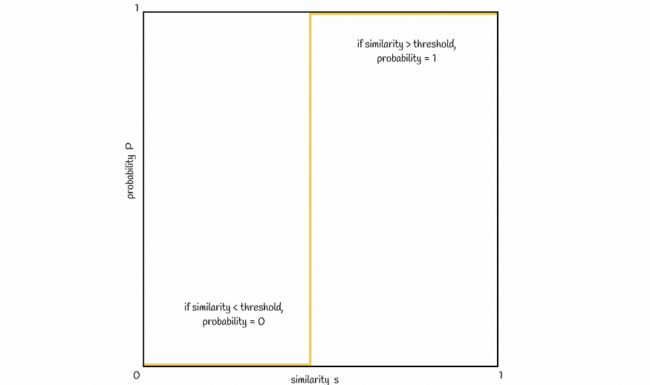
        现在让我们可视化两个签名成为候选者的相似性 s 和概率 P 之间的联系。通常，签名相似度越高，签名成为候选者的可能性就越高。理想情况下，它如下所示：

        理想的场景。只有当一对签名的相似性大于某个阈值 t 时，它们才被视为候选签名

        根据上面获得的概率公式，一条典型的线如下图所示：

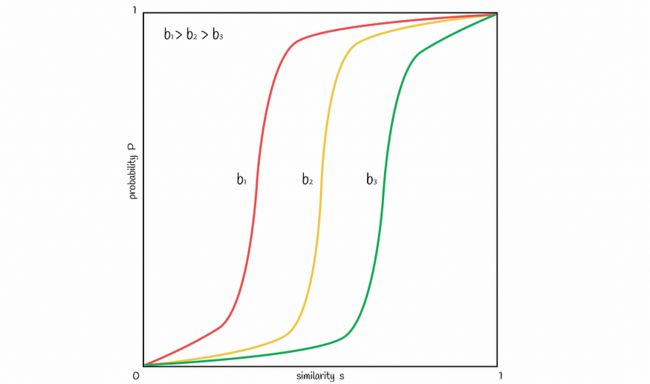
        一条典型的直线，在开始和结束时缓慢增加，并且在图中近似概率公式给出的阈值 t 处具有陡峭的斜率

        可以改变波段 b 的数量，以将图中的线向左或向右移动。增加 b 将线向左移动并导致更多的 FP，减少 — 将其向右移动并导致更多的 FN。根据问题找到良好的平衡很重要。

        波段数越多，线向左移动，越低 — 向右移动

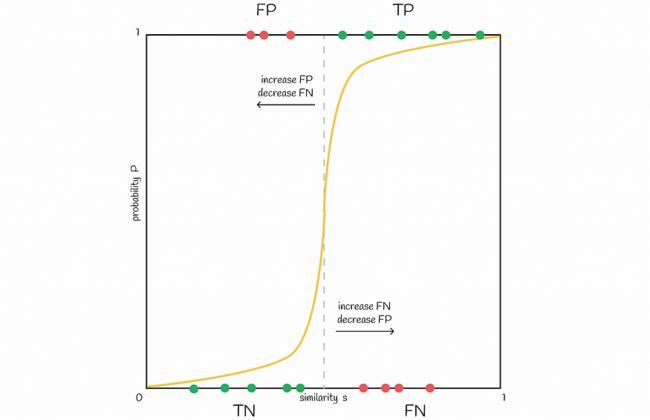
将阈值向左移动会增加 FP，而向右移动阈值会增加 FN

5.3 使用不同数量的波段和行进行实验

        下面针对 b 和 r 的不同值构建了几个线图。最好根据特定任务调整这些参数，以成功检索所有相似文档对，并忽略具有不同签名的文档对。

        调整波段数

调整行数

六、结论

        我们已经演练了 LSH 方法的经典实现。利星行通过使用低维签名表示和快速散列机制来缩小候选人的搜索范围，从而显著优化了搜索速度。同时，这是以牺牲搜索准确性为代价的，但在实践中，差异通常微不足道。

        然而，LSH 容易受到高维数据的影响：更多的维度需要更长的签名长度和更多的计算来保持良好的搜索质量。在这种情况下，建议使用另一个索引。

        事实上，LSH存在不同的实现，但它们都基于相同的范式，即将输入向量转换为哈希值，同时保留有关其相似性的信息。基本上，其他算法只是定义获取这些哈希值的其他方法。

        随机投影是另一种 LSH 方法，将在下一章中介绍，该方法在 Faiss 库中作为 LSH 索引实现，用于相似性搜索。

资源

• 局部敏感哈希 |安德鲁·威利 |十二月 2， 2013
• 数据挖掘 |局部敏感哈希 |塞格德大学
• 费斯存储库