机器学习基础 - 使用sklearn构建完整的机器学习项目流程

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

机器学习一般都有以下几个步骤：
1.确定任务类型，回归 or 分类
2.收集数据集并选择合适的特征
3.选择度量模型性能的指标
4.选择模型，拟合数据，评估性能及参数调优

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、收集数据并选择合适特征

在数据集上我们使用我们之前使用过的乳腺癌病例数据集

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
plt.style.use('ggplot')
import seaborn as sns
from sklearn import datasets
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from pygam import LinearGAM
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline

# 收集数据并选择特征
diabetes = datasets.load_diabetes()
x = diabetes.data
y = diabetes.target
features = diabetes.feature_names
diabetes_data = pd.DataFrame(x, columns=features)
diabetes_data['ill_degree'] = y
print(diabetes_data.head())

二、选择度量模型性能的指标

一般来说可选用如上的各种性能指标，本文选择最熟悉的mse

三、选择模型拟合样本

假设X和Y之间存在线性关系，模型的具体形式为


在拟合样本后，可以使用最小二乘法来描述回归模型与真实情况之间的差距，

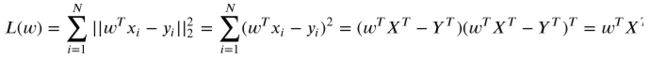
此时仅需找出让L最大的参数w就能使得L最小，这时求导可解决问题

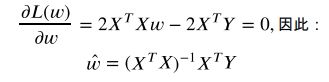
# 训练线性回归模型
lin_reg = linear_model.LinearRegression()
lin_reg.fit(x, y)
print('模型系数：', lin_reg.coef_)
print('模型得分：', lin_reg.score(x, y))

在线性回归中，我们假设因变量与特征之间的关系是线性关系，这样的假设使得模型很简单，但
是缺点也是显然的，那就是当数据存在非线性关系时，我们使用线性回归模型进行预测会导致预
测性能极其低下，因为模型的形式本身是线性的，无法表达数据中的非线性关系。我们一个很自
然的想法就是去推广线性回归模型，使得推广后的模型更能表达非线性的关系。

多项式回归

为了体现因变量和特征的非线性关系，一个很自然而然的想法就是将标准的线性回归模型

换成一个多项式函数

对于多项式的阶数d不能取过大，一般不大于3或者4，因为d越大，多项式曲线就会越光滑，在X
的边界处有异常的波动。（图中的边界处的4阶多项式拟合曲线的置信区间(虚线表示置信区间)明
显增大，预测效果的稳定性下降。）

## 线性回归推广 --多项式回归
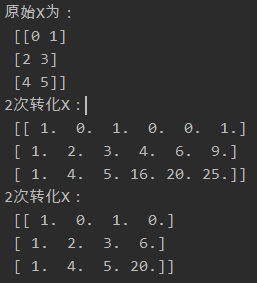
x_arr = np.arange(6).reshape(3, 2)
print('原始X为：\n', x_arr)
poly = PolynomialFeatures(2)
print('2次转化X：\n', poly.fit_transform(x_arr))
poly = PolynomialFeatures(interaction_only=True)
print('2次转化X：\n', poly.fit_transform(x_arr))

广义可加模型

广义可加模型GAM实际上是线性模型推广至非线性模型的一个框架，在这个框架中，每一个变量
都用一个非线性函数来代替，但是模型本身保持整体可加性。GAM模型不仅仅可以用在线性回归
的推广，还可以将线性分类模型进行推广。具体的推广形式是：
标准的线性回归模型：

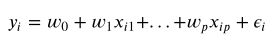
GAM模型框架：

## 广义可加模型GAM
gam = LinearGAM().fit(diabetes_data[diabetes.feature_names], y)
print(gam.summary())

LinearGAM                                                                                                 
=============================================== ==========================================================
Distribution:                        NormalDist Effective DoF:                                     92.0369
Link Function:                     IdentityLink Log Likelihood:                                 -3893.2146
Number of Samples:                          442 AIC:                                             7972.5028
                                                AICc:                                            8022.7891
                                                GCV:                                             4208.5528
                                                Scale:                                           2668.0171
                                                Pseudo R-Squared:                                   0.6438
==========================================================================================================
Feature Function                  Lambda               Rank         EDoF         P > x        Sig. Code   
================================= ==================== ============ ============ ============ ============
s(0)                              [0.6]                20           13.5         4.96e-02     *           
s(1)                              [0.6]                20           4.9          1.44e-03     **          
s(2)                              [0.6]                20           11.4         1.31e-09     ***         
s(3)                              [0.6]                20           11.2         1.29e-01                 
s(4)                              [0.6]                20           11.5         4.30e-02     *           
s(5)                              [0.6]                20           8.0          5.97e-02     .           
s(6)                              [0.6]                20           9.5          3.26e-01                 
s(7)                              [0.6]                20           6.9          1.48e-01                 
s(8)                              [0.6]                20           7.7          1.79e-07     ***         
s(9)                              [0.6]                20           7.4          4.34e-03     **          
intercept                                              1            0.0          1.18e-01                 
==========================================================================================================
Significance codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

WARNING: Fitting splines and a linear function to a feature introduces a model identifiability problem
         which can cause p-values to appear significant when they are not.

WARNING: p-values calculated in this manner behave correctly for un-penalized models or models with
         known smoothing parameters, but when smoothing parameters have been estimated, the p-values
         are typically lower than they should be, meaning that the tests reject the null too readily.
None

GAM模型的优点与不足：
优点：简单容易操作，能够很自然地推广线性回归模型至非线性模型，使得模型的预测精度
有所上升；由于模型本身是可加的，因此GAM还是能像线性回归模型一样把其他因素控制不
变的情况下单独对某个变量进行推断，极大地保留了线性回归的易于推断的性质。
缺点：GAM模型会经常忽略一些有意义的交互作用，比如某两个特征共同影响因变量，不过
GAM还是能像线性回归一样加入交互项 的形式进行建模；但是GAM模型本质上还
是一个可加模型，如果我们能摆脱可加性模型形式，可能还会提升模型预测精度，详情请看
后面的算法。

回归树

基于树的回归方法主要是依据分层和分割的方式将特征空间划分为一系列简单的区域。对某个给
定的待预测的自变量，用他所属区域中训练集的平均数或者众数对其进行预测。由于划分特征空
间的分裂规则可以用树的形式进行概括，因此这类方法称为决策树方法。决策树由结点(node)和
有向边(diredcted edge)组成。结点有两种类型：内部结点(internal node)和叶结点(leaf node)。内
部结点表示一个特征或属性，叶结点表示一个类别或者某个值。区域 等称为叶节点，将特
征空间分开的点为内部节点。
建立回归树的过程大致可以分为以下两步：
将自变量的特征空间(即 )的可能取值构成的集合分割成J个互不重叠
的区域 。
对落入区域 的每个观测值作相同的预测，预测值等于 上训练集的因变量的简单算术平
均。

## 回归树
reg_tree =DecisionTreeRegressor(criterion='mse', min_samples_leaf=5)
reg_tree.fit(x, y)
print(reg_tree.score(x, y))

支持向量机

在线性回归的理论中，每个样本点都要计算平方损失，但是SVR却是不一样的。SVR认为：落在
的f(x)邻域空间中的样本点不需要计算损失，这些都是预测正确的，其余的落在E邻域空间以外
的样本才需要计算损失，因此引入拉格朗日函数，再令L对

求偏导，即要求

## 支持向量机回归
reg_svr = make_pipeline(StandardScaler(), SVR(C=1121.0, epsilon=0.1))
reg_svr.fit(x, y)
print(reg_svr.score(x, y))

---