AtCoder ABC324 B~E赛后补题

赛时没有写出E，早上补完E

B - 3-smooth Numbers

B - 3-smooth Numbers (atcoder.jp)

题面

题面翻译与思路

判断某个数是否能表示为$2^x{3}^y$

当n%2==0或者n%3==0时，相应地，将这个数不断地除2或者3，判断最后n是否为1
(t了一发，因为写了统计n的质因子个数，瞬间反应过来是想复杂了)

代码

void solve()
{
    LL n; cin >> n;
    while (n % 2 == 0) n /= 2;
    while (n % 3 == 0) n /= 3;
    if (n != 1) cout << "No\n";
    else cout << "Yes\n";
}

---

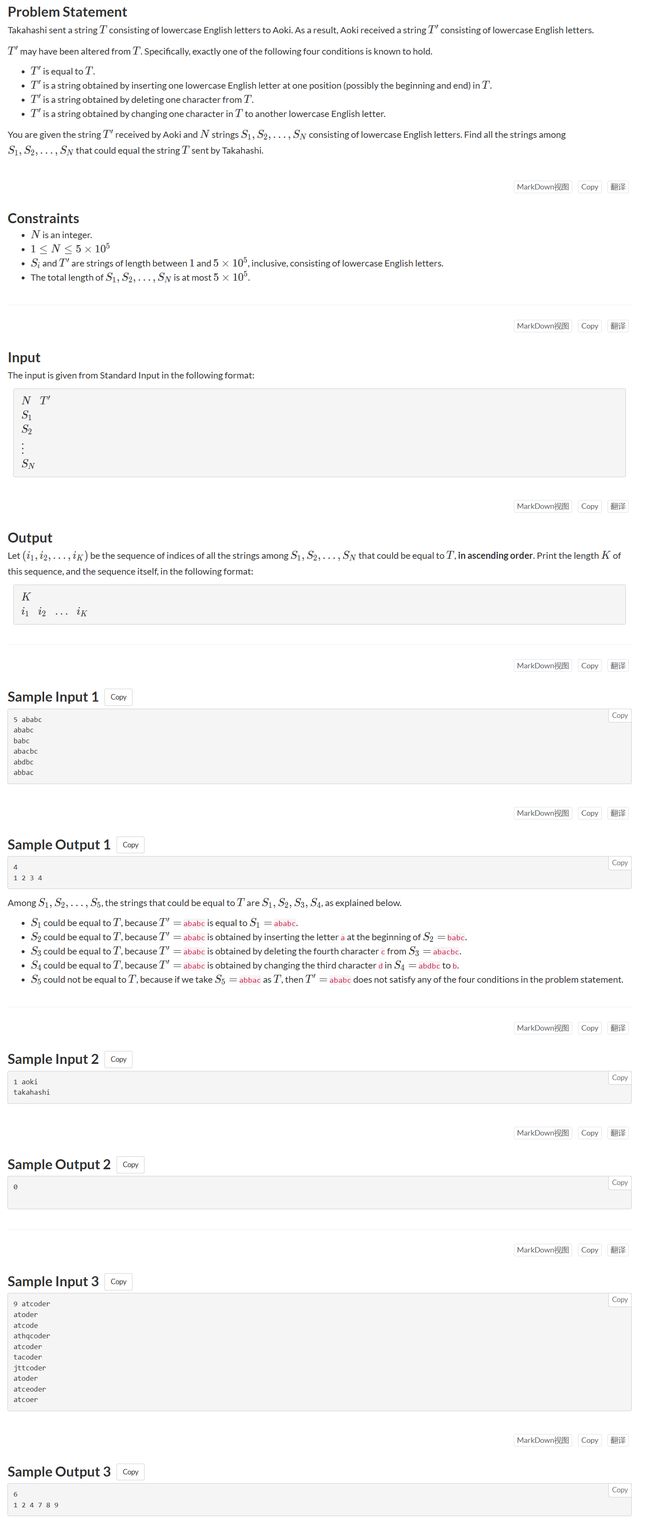
C - Error Correction

C - Error Correction (atcoder.jp)

题面

题面翻译与思路

给定t串与一组字符串strs，对于t串和strs中的每个字符串s，判断是否"相等"。
"相等"包括：

• s = t
• len(s) = len(t)，但相应的位置上只能有一个字符不同
• len(s) = len(t) + 1，在t的任意位置添加一个字符后，与s相等
• len(s) + 1 = len(t)，在t的任意位置删除一个字符后，与s相等

分三种情况判断，用i和j双指针遍历s串和t串：

1. len(s) = len(t)，统计不同字符的个数cnt，若cnt>1则不"相等"
2. len(s) = len(t) + 1 ，统计不同字符的个数cnt，遇到不同字符时t的指针向后走，s的指针不动，最后cnt>1则不"相等"
3. len(s) + 1 = len(t) ，统计不同字符的个数cnt，遇到不同字符时s的指针向后走，t的指针不动，最后cnt>1则不"相等"

当然两字符串的长度相差超过1，直接不"相等"，不同进行上面的判断

代码

#include 
using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef unsigned long long ULL;
const int inf = 2e9 + 10;
const LL INF = 4e18 + 10;
const int mod9 = 998244353;
const int mod7 = 1e9 + 7;
const int N = 2e5 + 10;
string t; int n; 

bool check(string& s)
{
    if (abs((int)t.size() - (int)s.size()) > 1) return false;
    int cnt = 0;
    if (t.size() == s.size())
    {
        for (int i = 0; i < t.size(); ++ i)
        {
            if (t[i] != s[i]) cnt ++ ;
        }
    }
    else if (t.size() + 1 == s.size())
    {
        int i = 0, j = 0;
        while (i < t.size() && j < s.size())
        {
            if (t[i] != s[j]) j ++ , cnt ++ ;
            else ++ i, ++ j;
        }
    }
    else if (t.size() == s.size() + 1)
    {
        int i = 0, j = 0;
        while (i < t.size() && j < s.size())
        {
            if (t[i] != s[j]) i ++ , cnt ++ ;
            else ++ i, ++ j;
        }
    }
    if (cnt > 1) return false;
    return true;
}

void solve()
{
    vector<int> ans;
    cin >> n >> t;
    for (int i = 1; i <= n; ++ i)
    {
        string s; cin >> s;    
        if (check(s)) ans.push_back(i);
    }
    cout << ans.size() << "\n";
    for (auto t : ans) cout << t << ' ';
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0),cout.tie(0);
    solve();
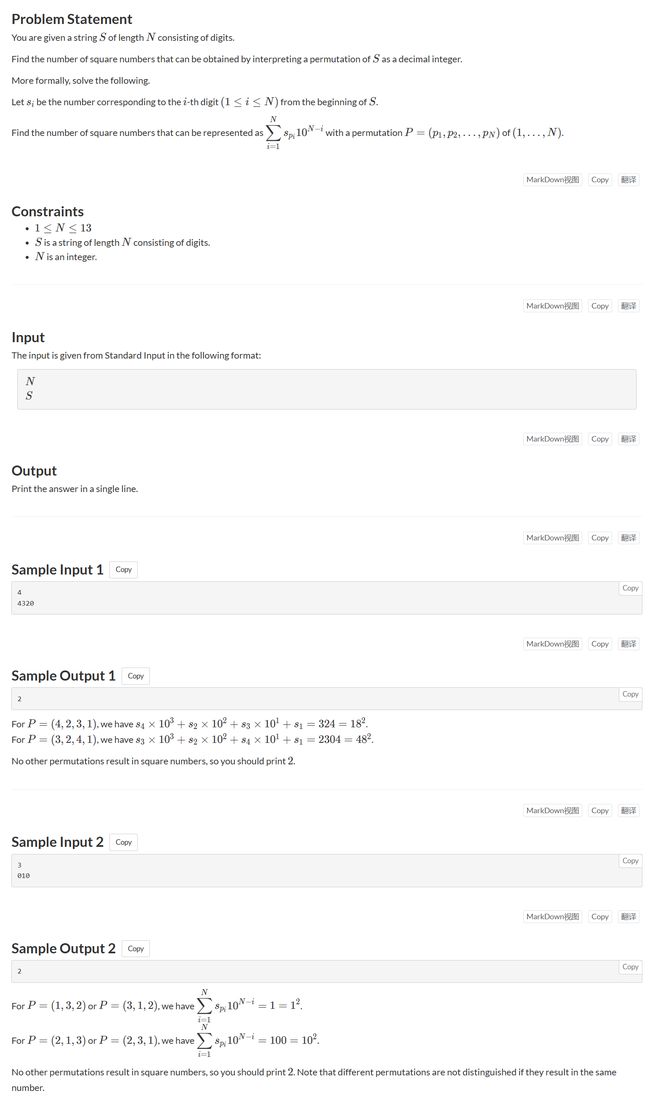
    return 0;
}

---

D - Square Permutation

D - Square Permutation (atcoder.jp)

题面

题面翻译与思路

以字符串的形式给你一个整数x，将x的每一位看成独立的数字进行全排列，如"123"的全排列为：123，132，213，231，312，321（吐槽下题目给的公式太抽象了）
问这些全排列中，有几个数可以表示为某个数的平方（sqrt运算的结果为整数）？

反着考虑，枚举平方数（$1^2$,$2^2$,$3^2$…)，判断该平方数是否为x的全排列
如何判断？计算平方数的每个数字的出现次数（112中，1出现2次，2出现1次），判断平方数的1_{9出现次数为x的1}9出现次数是否相等（可以证明，不用考虑0的出现次数）
假设x为4位数，当平方数大于9999时就不需要枚举下去了

注意特判x为0的情况，0的平方为0，所以应该输出1

代码

#include 
using namespace std;

typedef long long LL;
int cnt[20];

void solve()
{
    int n; string s; cin >> n >> s;
    if (s == "0") { cout << 1; return; }
    for (auto t : s) cnt[t - '0'] ++ ;
    LL ans = 0;
    for (LL i = 1; i * i <= pow(10, s.size()) - 1; ++ i)
    {
        LL b = i * i;
        LL t = i * i;
        int tmp[20] = {0};
        while (t) 
        {
            tmp[(t % 10)] ++ ;
            t /= 10;
        }
        bool flag = true;
        for (int i = 1; i <= 9; ++ i) 
            if (cnt[i] != tmp[i])
            {
                flag = false;
                break;
            }
            
        if (flag) ans ++ ;
    }
    cout << ans << "\n";
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0),cout.tie(0);
    solve();
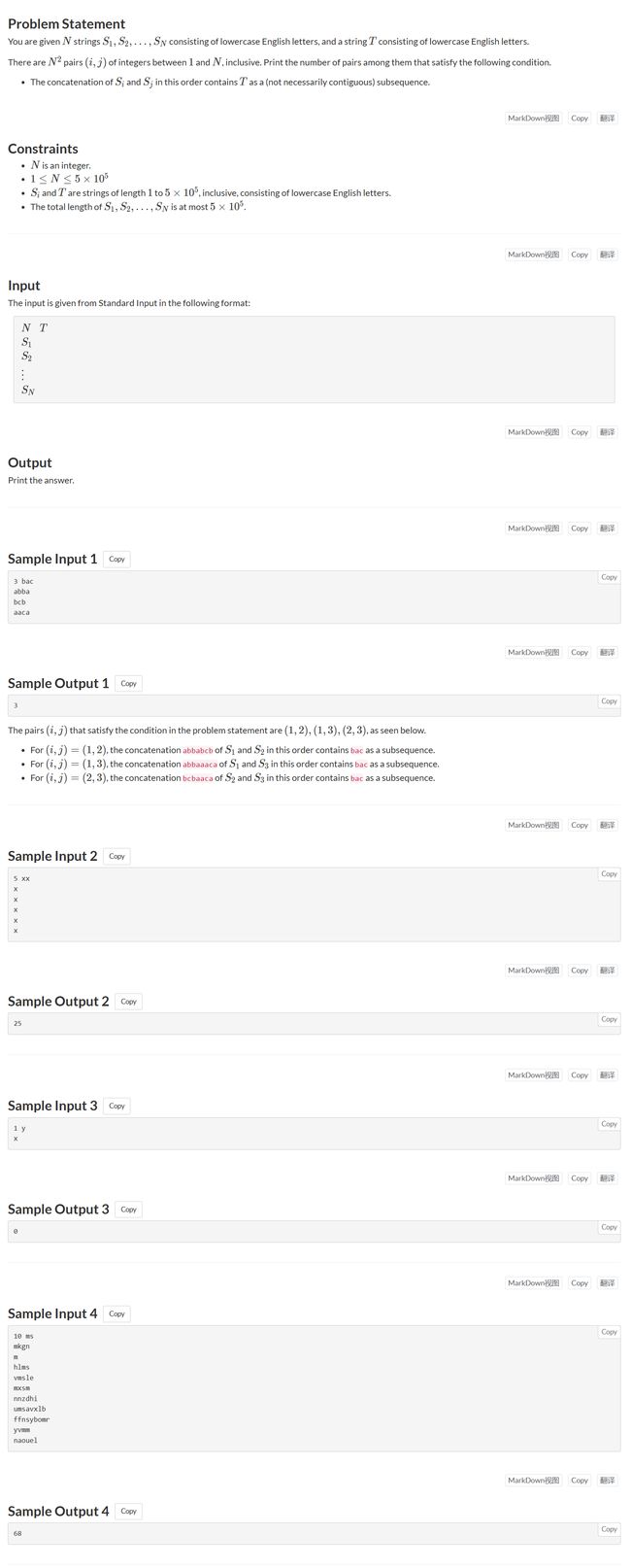
    return 0;
}

---

E - Joint Two Strings

E - Joint Two Strings (atcoder.jp)

题面

题面翻译与思路

给定t和一组字符串strs，选择strs中的两个字符串进行拼接，问有多少个拼接后的字符串满足条件：其子序列和t相等

两个字符串的拼接，很容易想到预处理前后缀。若一个字符串的子序列包含了t的前缀，一个字符串的子序列包含了t的后缀，且长度相加大于t的长度，那么这两个字符串的拼接就是满足题意的
所以对于strs中的每个字符串str，预处理str的两个"最长子序列"的长度，这两个"子序列"分别需要与t的前缀和后缀相等并且最长

如：t = bac, str = abba
一个最长子序列为"ba"，该子序列与t的前缀"ba"相等并且最长（t的前缀为"“,“b”,“ba”,“bac”）
另一个最长子序列为”“，该子序列与t的后缀”“相等并且最长（t的后缀为”",“c”,“ca”,“cab”）

开pre和suf两个一维数组分别记录第i个str的两个最长子序列长度
再开一个一维数组scnt记录：strs中，与t后缀相等的最长子序列，长度i的出现次数，如scnt[5] = 3表示strs中，与t后缀相等且长度为5的最长子序列出现了3次
对scnt进行后向求和，即一个str包含了长度为m且与t后缀相等的子序列，那么一定包含长度为[0, m]且与t后缀相等的子序列
如果一个str包含了长度为m且与t前缀相等的子序列，那么与满足以下条件的字符串拼接，答案+1：包含长度大于等于t.size() - m且与t后缀相等的子序列
那么，线性遍历pre数组即可求出答案

代码

#include 
using namespace std;

typedef long long LL;
const int N = 5e5 + 10;
int pre[N], suf[N], scnt[N];

void solve()
{
    int n; string t; cin >> n >> t;
    for (int k = 1; k <= n; ++ k)
    {
        string s; cin >> s;
        int i, j;
        for (i = 0, j = 0; i < s.size() && j < t.size(); ++ i) if (s[i] == t[j]) ++ j ;
        pre[k] = j;
        for (i = s.size() - 1, j = t.size() - 1; i >= 0 && j >= 0; -- i) if (s[i] == t[j]) -- j ;
        suf[k] = t.size() - j - 1;
        scnt[suf[k]] ++ ;
    }
    for (int i = t.size() - 1; i >= 0; -- i) scnt[i] += scnt[i + 1];
    LL ans = 0;
    for (int i = 1; i <= n; ++ i) ans += scnt[t.size() - pre[i]];
    cout << ans << "\n";
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0),cout.tie(0);
    solve();
    return 0;
}