机器学习之线性回归
机器学习之线性回归
- 1 机器学习基本概念
-
- 1.1 定义:
- 1.2分类
-
- 1.2.1有监督学习
- 1.2.2 无监督学习
- 1.3 模型泛化能力
- 1.4 模型可能出现的问题:
-
- 1.4.1 过拟合问题(high variance)
- 1.4.2 欠拟合问题(high bias)
- 1.5 交叉验证
- 2 线性回归基本原理
-
- 2.1 线性回归定义
- 2.2 一元回归(单个特征)
- 2.2 多元回归(即多个特征)
- 3 损失函数 代价函数、目标函数
- 4 优化方法
-
- 4.1 梯度下降
- 4.2 牛顿法及拟牛顿法
- 5 线性回归评价指标
1 机器学习基本概念
1.1 定义:
对于某个特定任务,从数据中学出一个模型,用某种衡量方式来表示该模型性能。
For task ,learn from E(experience) ,measure by P(performance.
1.2分类
1.2.1有监督学习
有监督学习:对训练数据,每个样本具有特征(或者属性),且带有标签。
有监督学习主要包含两类问题:回归问题和分类问题。
回归问题:如预测房价。房价由房子本身的特征(如大小,面积,房间个数等),因为任务是房价预测,那么此时的标签也就是房子的价格:房价。
分类问题:如预测肿瘤是良性还是恶性。此时只有只有两种可能,良性还是恶性。
此时特征可能有(肿瘤大小、形状等),标签就是良性肿瘤或者恶性肿瘤,一般数据中表现为1或者0(对于二分类),而对于多分类,可能需要进行独热编码。
本次主要说回归问题中的线性回归。
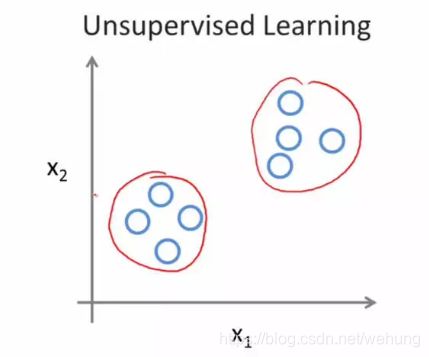
1.2.2 无监督学习
给定数据,不带有标签。
如进行市场划分任务,可以通过聚类算法或者其他方式将市场划分为那几个类
1.3 模型泛化能力
泛化能力:指的机器学习所学模型对新鲜样本的适应能力。若泛化能力好,则证明该模型适应性强,反之,则表现差。
如何衡量模型的泛化能力呢?
通常不同任务对模型的泛化衡量标准不一样。
训练出模型后,通常在验证集上进行超参数选择,不断调整,最后再测试集上看自己的泛化性能。
对于回归问题:
衡量指标:
- MSE(均方误差)
- RMSE(均方根误差)
- MAE (平均绝对误差)
- R Squard(R方)
- Adjusted R-square(矫正决定系数)等
对于分类问题
衡量指标
- 准确率 (accuracy)
- 查全率 (precision)
- 召回率(recall)
- F1 score等
1.4 模型可能出现的问题:
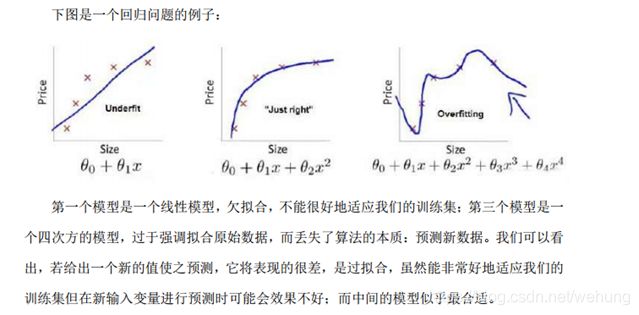
1.4.1 过拟合问题(high variance)
过拟合问题:是指模型太过复杂,对训练数据效果好,而对新样本泛化能力较弱。
(训练误差低 验证误差高)
产生过拟合的可能原因,可能为其中之一或者都有:
- 模型的复杂度过高。如网络太深,神经网络中;或者线性回归中模型的阶次
- 过多的变量特征
- 训练数据过少
如何解决过拟合: - 降低模型复杂度
- 减少特征数目
- 增加数据
- 正则化等
1.4.2 欠拟合问题(high bias)
欠拟合:指模型太过简单,不能对训练数据效果不好,对新样本泛化能力也不好。
如何解决欠拟合
- 增加模型复杂度
- 添加特征
- 增加数据
- 减少正则化参数大小等
1.5 交叉验证
一般对于一个机器学习问题,通常把数据集分为训练集、验证集、测试集。
其中:
训练集:用来训练模型参数。如线性模型中的theta向量。
验证集:为了验证在训练集中的参数是否具有良好的性能,故设置验证集。训练出多组超参数后,在验证集中验证,选取性能较好参数。
测试集:用来测试模型的泛化性能,看是否满足相关性能要求。
2 线性回归基本原理
2.1 线性回归定义
回归是监督学习的一个重要问题,回归用于预测输入变量和输出变量之间的关系。
回归模型是表示输入变量到输出变量之间映射的函数。
本质上回归问题的学习等价于函数拟合:使用一条函数曲线使其很好的拟合已知函数且很好的预测未知数据。https://www.cnblogs.com/futurehau/p/6105011.html
2.2 一元回归(单个特征)
2.2 多元回归(即多个特征)
3 损失函数 代价函数、目标函数
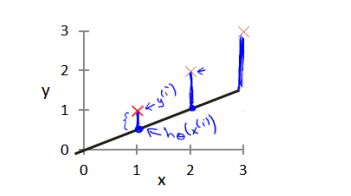
线性最常用回归损失函数(对单个样本):
![]()
代价函数(对所有样本(当前数据))
![]()
线性回归目标函数
![]()
4 优化方法
4.1 梯度下降
基本思想:
可以类比为一个下山的过程,即往当前上坡的反方向即可。参考见吴恩达老师《machine learning》
缺点:
若函数不为凸函数,可能找到局部最小值
批梯度下降公式:

以仅有两个参数举例:
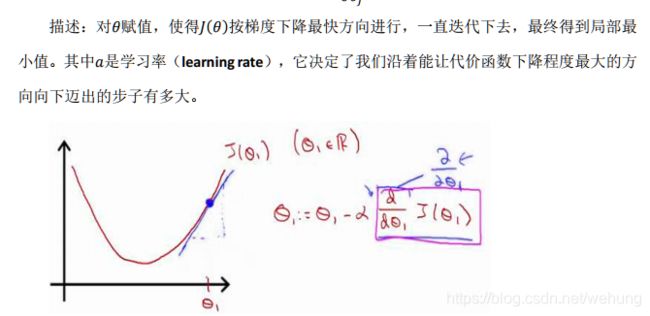
(参考吴恩达老师pdf 第一周)
α过小 ,若训练的epoch过小 ,则可能不能收敛;若够大,可能会收敛的比较慢
α过大 ,可能波动震荡 无法收敛 ,甚至发散
4.2 牛顿法及拟牛顿法
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。
可参考:
https://blog.csdn.net/itplus/article/details/21896453
拟牛顿法
可参考如上链接https://blog.csdn.net/itplus/article/details/21896453
5 线性回归评价指标
1 MSE(均方误差,常用于回归,其本身为凸函数)

但又有一个问题,之前算这个公式时为了保证其每项为正,且可导(所以没用绝对值的表示方法),我们对式子加了一个平方。但这可能会导致量纲的问题,如房子价格为万元,平方后就成了万元的平方。
2. RMSE(均方根误差):
对MSE进行开方
3.MAE(Mean Absolute Error)

3. R Squard(R方)
上面的几种衡量标准针对不同的模型会有不同的值。比如说预测房价 那么误差单位就是万元。数子可能是3,4,5之类的。那么预测身高就可能是0.1,0.6之类的。没有什么可读性,到底多少才算好呢?不知道,那要根据模型的应用场景来。
看看分类算法的衡量标准就是正确率,而正确率又在0~1之间,最高百分之百。最低0。如果是负数,则考虑非线性相关。很直观,而且不同模型一样的。那么线性回归有没有这样的衡量标准呢?答案是有的。

4. Adjusted R-square(矫正决定系数)

6 Sklearn 线性回归参数详解
sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

普通的最小均方线性回归:
参数解释:
fit_intercept:布尔值,可选,默认值为True
是否计算此模型的截距(b如.设置为False,则不会在计算中使用截距(例如,数据此时已经中心化)
normalize : 布尔值,可选,默认值为False
当fit_intercept设置为False时,将忽略此参数。 如果为True,则回归量X将在回归之前通过减去平均值并除以L2范数来归一化,。 如果你希望标准化数据集, 那么在使用估计器(并将估计器normalize参数设置为False)前使用sklearn.preprocessing.StandardScaler这个函数.
copy_X : 参数只可设置为True或False, 默认为True.
如果为True, 数据集X将会被复制,若为False, 原始数据会被覆盖.
n_jobs:int或None,可选(无默认)
用于计算的CPU数目。 这只会为n_targets> 1和足够大的问题提供加速。 除非在joblib.parallel_backend上下文中,否则表示1。 -1表示使用所有处理器。 有关详细信息,请参阅词汇表。
from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
reg.coef_
array([0.5, 0.5])
参考资料:
吴恩达 《机器学习》第一周教学资料
sklearn官方文档https://scikit-learn.org/stable/modules/linear_model.html#ordinary-least-squares-complexity
以及文章中博客链接资料。
如有未提到的博客链接,请联系我,谢谢。