GIS理论(墨卡托投影、地理坐标系、地面分辨率、地图比例尺、Bing Maps Tile System)
墨卡托投影(Mercator Projection),又名“等角正轴圆柱投影”,荷兰地图学家墨卡托(Mercator)在1569年拟定,假设地球被围在一个中空的圆柱里,其赤道与圆柱相接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅标准纬线为零度(即赤道)的“墨卡托投影”绘制出的世界地图。
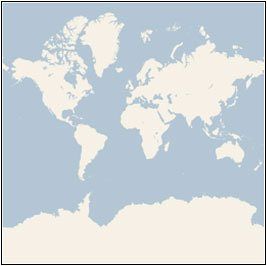
一、墨卡托投影坐标系(Mercator Projection)
墨卡托投影以整个世界范围,赤道作为标准纬线,本初子午线作为中央经线,两者交点为坐标原点,向东向北为正,向西向南为负。南北极在地图的正下、上方,而东西方向处于地图的正右、左。
由于Mercator Projection在两极附近是趋于无限值得,因此它并没完整展现了整个世界,地图上最高纬度是85.05度。为了简化计算,我们采用球形映射,而不是椭球体形状。虽然采用Mercator Projection只是为了方便展示地图,需要知道的是,这种映射会给Y轴方向带来0.33%的误差。

由于赤道半径为6378137米,则赤道周长为2*PI*r = 20037508.3427892,因此X轴的取值范围:[-20037508.3427892,20037508.3427892]。当纬度φ接近两极,即90°时,Y值趋向于无穷。因此通常把Y轴的取值范围也限定在[-20037508.3427892,20037508.3427892]之间。因此在墨卡托投影坐标系(米)下的坐标范围是:最小为(-20037508.3427892, -20037508.3427892 )到最大 坐标为(20037508.3427892, 20037508.3427892)。
二、地理坐标系(Geographical coordinates)
地理经度的取值范围是[-180,180],纬度不可能到达90°,通过纬度取值范围为[20037508.3427892,20037508.3427892]反计算可得到纬度值为85.05112877980659。因此纬度取值范围是[-85.05112877980659,85.05112877980659]。因此,地理坐标系(经纬度)对应的范围是:最小地理坐标(-180,-85.05112877980659),最大地理坐标(180, 85.05112877980659)。
三、地面分辨率(Ground Resolution)
地面分辨率是以一个像素(pixel)代表的地面尺寸(米)。以微软Bing Maps为例,当Level为1时,图片大小为512*512(4个Tile),那么赤道空间分辨率为:赤道周长/512。其他纬度的空间分辨率则为 纬度圈长度/512,极端的北极则为0。Level为2时,赤道的空间分辨率为 赤道周长/1024,其他纬度为 纬度圈长度1024。很明显,Ground Resolution取决于两个参数,缩放级别Level和纬度latitude ,Level决定像素的多少,latitude决定地面距离的长短。
地面分辨率的公式为,单位:米/像素:
ground resolution = (cos(latitude * pi/180) * 2 * pi * 6378137 meters) / (256 * 2level pixels)
最低地图放大级别(1级),地图是512 x 512像素。每下一个放大级别,地图的高度和宽度分别乘于2:2级是1024 x 1024像素,3级是2048 x 2048像素,4级是4096 x 4096像素,等等。通常而言,地图的宽度和高度可以由以下式子计算得到:map width = map height = 256 * 2^level pixels
四、地图比例尺(Map Scale)
地图比例尺是指测量相同目标时,地图上距离与实际距离的比例。通过地图分辨率在计算可知由Level可得到图片的像素大小,那么需要把其转换为以米为单位的距离,涉及到DPI(dot per inch),暂时可理解为类似的PPI(pixelper inch),即每英寸代表多少个像素。256 * 2level / DPI 即得到相应的英寸inch,再把英寸inch除以0.0254转换为米。实地距离仍旧是:cos(latitude * pi/180) * 2 * pi * 6378137 meters; 因此比例尺的公式为:
map scale = 256 * 2level / screen dpi / 0.0254 / (cos(latitude * pi/180) * 2 * pi * 6378137)
比例尺= 1 : (cos(latitude * pi/180) * 2 * pi * 6378137 * screen dpi) / (256 * 2level * 0.0254)
地面分辨率和地图比例尺之间的关系:
map scale = 1 : ground resolution * screen dpi / 0.0254 meters/inch
| 缩放级别 |
地图宽度、高度(像素) |
地面分辨率(米/像素) |
地图比例尺(以96dpi为例) |
| 1 |
512 |
78,271.5170 |
1 : 295,829,355.45 |
| 2 |
1,024 |
39,135.7585 |
1 : 147,914,677.73 |
| 3 |
2,048 |
19,567.8792 |
1 : 73,957,338.86 |
| 4 |
4,096 |
9,783.9396 |
1 : 36,978,669.43 |
| 5 |
8,192 |
4,891.9698 |
1 : 18,489,334.72 |
| 6 |
16,384 |
2,445.9849 |
1 : 9,244,667.36 |
| 7 |
32,768 |
1,222.9925 |
1 : 4,622,333.68 |
| 8 |
65,536 |
611.4962 |
1 : 2,311,166.84 |
| 9 |
131,072 |
305.7481 |
1 : 1,155,583.42 |
| 10 |
262,144 |
152.8741 |
1 : 577,791.71 |
| 11 |
524,288 |
76.4370 |
1 : 288,895.85 |
| 12 |
1,048,576 |
38.2185 |
1 : 144,447.93 |
| 13 |
2,097,152 |
19.1093 |
1 : 72,223.96 |
| 14 |
4,194,304 |
9.5546 |
1 : 36,111.98 |
| 15 |
8,388,608 |
4.7773 |
1 : 18,055.99 |
| 16 |
16,777,216 |
2.3887 |
1 : 9,028.00 |
| 17 |
33,554,432 |
1.1943 |
1 : 4,514.00 |
| 18 |
67,108,864 |
0.5972 |
1 : 2,257.00 |
| 19 |
134,217,728 |
0.2986 |
1 : 1,128.50 |
| 20 |
268,435,456 |
0.1493 |
1 : 564.25 |
| 21 |
536,870,912 |
0.0746 |
1 : 282.12 |
| 22 |
1,073,741,824 |
0.0373 |
1 : 141.06 |
| 23 |
2,147,483,648 |
0.0187 |
1 : 70.53 |
五、Bing Maps像素坐标系和地图图片编码
为了优化地图系统性能,提高地图下载和显示速度,所有地图都被分割成256 x 256像素大小的正方形小块。由于在每个放大级别下的像素数量都不一样,因此地图图片(Tile)的数量也不一样。每个tile都有一个XY坐标值,从左上角的(0, 0)至右下角的(2^level–1, 2^level–1)。例如在3级放大级别下,所有tile的坐标值范围为(0, 0)至(7, 7),如下图:

已知一个像素的XY坐标值时,我们很容易得到这个像素所在的Tile的XY坐标值:
tileX = floor(pixelX / 256) tileY = floor(pixelY / 256)
为了简化索引和存储地图图片,每个tile的二维XY值被转换成一维字串,即四叉树键值(quardtree key,简称quadkey)。每个quadkey独立对应某个放大级别下的一个tile,并且它可以被用作数据库中B-tree索引值。为了将坐标值转换成quadkey,需要将Y和X坐标二进制值交错组合,并转换成4进制值及对应的字符串。例如,假设在放大级别为3时,tile的XY坐标值为(3,5),quadkey计算如下:
tileX = 3 = 011(二进制)
tileY = 5 = 101(二进制)
quadkey = 100111(二进制) = 213(四进制) = “213”
Quadkey还有其他一些有意思的特性。第一,quadkey的长度等于该tile所对应的放大级别;第二,每个tile的quadkey的前几位和其父tile(上一放大级别所对应的tile)的quadkey相同,下图中,tile 2是tile 20至23的父tile,tile 13是tile 130至133的父级:

最后,quadkey提供的一维索引值通常显示了两个tile在XY坐标系中的相似性。换句话说,两个相邻的tile对应的quadkey非常接近。这对于优化数据库的性能非常重要,因为相邻的tile通常被同时请求显示,因此可以将这些tile存放在相同的磁盘区域中,以减少磁盘的读取次数。
下面是微软Bing Maps的TileSystem相关算法:
using System.Text;
namespace Microsoft.MapPoint
{
static class TileSystem
{
private const double EarthRadius = 6378137 ;
private const double MinLatitude = - 85.05112878 ;
private const double MaxLatitude = 85.05112878 ;
private const double MinLongitude = - 180 ;
private const double MaxLongitude = 180 ;
/// <summary>
/// Clips a number to the specified minimum and maximum values.
/// </summary>
/// <param name="n"> The number to clip. </param>
/// <param name="minValue"> Minimum allowable value. </param>
/// <param name="maxValue"> Maximum allowable value. </param>
/// <returns> The clipped value. </returns>
private static double Clip( double n, double minValue, double maxValue)
{
return Math.Min(Math.Max(n, minValue), maxValue);
}
/// <summary>
/// Determines the map width and height (in pixels) at a specified level
/// of detail.
/// </summary>
/// <param name="levelOfDetail"> Level of detail, from 1 (lowest detail)
/// to 23 (highest detail). </param>
/// <returns> The map width and height in pixels. </returns>
public static uint MapSize( int levelOfDetail)
{
return ( uint ) 256 << levelOfDetail;
}
/// <summary>
/// Determines the ground resolution (in meters per pixel) at a specified
/// latitude and level of detail.
/// </summary>
/// <param name="latitude"> Latitude (in degrees) at which to measure the
/// ground resolution. </param>
/// <param name="levelOfDetail"> Level of detail, from 1 (lowest detail)
/// to 23 (highest detail). </param>
/// <returns> The ground resolution, in meters per pixel. </returns>
public static double GroundResolution( double latitude, int levelOfDetail)
{
latitude = Clip(latitude, MinLatitude, MaxLatitude);
return Math.Cos(latitude * Math.PI / 180 ) * 2 * Math.PI * EarthRadius / MapSize(levelOfDetail);
}
/// <summary>
/// Determines the map scale at a specified latitude, level of detail,
/// and screen resolution.
/// </summary>
/// <param name="latitude"> Latitude (in degrees) at which to measure the
/// map scale. </param>
/// <param name="levelOfDetail"> Level of detail, from 1 (lowest detail)
/// to 23 (highest detail). </param>
/// <param name="screenDpi"> Resolution of the screen, in dots per inch. </param>
/// <returns> The map scale, expressed as the denominator N of the ratio 1 : N. </returns>
public static double MapScale( double latitude, int levelOfDetail, int screenDpi)
{
return GroundResolution(latitude, levelOfDetail) * screenDpi / 0.0254 ;
}
/// <summary>
/// Converts a point from latitude/longitude WGS-84 coordinates (in degrees)
/// into pixel XY coordinates at a specified level of detail.
/// </summary>
/// <param name="latitude"> Latitude of the point, in degrees. </param>
/// <param name="longitude"> Longitude of the point, in degrees. </param>
/// <param name="levelOfDetail"> Level of detail, from 1 (lowest detail)
/// to 23 (highest detail). </param>
/// <param name="pixelX"> Output parameter receiving the X coordinate in pixels. </param>
/// <param name="pixelY"> Output parameter receiving the Y coordinate in pixels. </param>
public static void LatLongToPixelXY( double latitude, double longitude, int levelOfDetail, out int pixelX, out int pixelY)
{
latitude = Clip(latitude, MinLatitude, MaxLatitude);
longitude = Clip(longitude, MinLongitude, MaxLongitude);
double x = (longitude + 180 ) / 360 ;
double sinLatitude = Math.Sin(latitude * Math.PI / 180 );
double y = 0.5 - Math.Log(( 1 + sinLatitude) / ( 1 - sinLatitude)) / ( 4 * Math.PI);
uint mapSize = MapSize(levelOfDetail);
pixelX = ( int ) Clip(x * mapSize + 0.5 , 0 , mapSize - 1 );
pixelY = ( int ) Clip(y * mapSize + 0.5 , 0 , mapSize - 1 );
}
/// <summary>
/// Converts a pixel from pixel XY coordinates at a specified level of detail
/// into latitude/longitude WGS-84 coordinates (in degrees).
/// </summary>
/// <param name="pixelX"> X coordinate of the point, in pixels. </param>
/// <param name="pixelY"> Y coordinates of the point, in pixels. </param>
/// <param name="levelOfDetail"> Level of detail, from 1 (lowest detail)
/// to 23 (highest detail). </param>
/// <param name="latitude"> Output parameter receiving the latitude in degrees. </param>
/// <param name="longitude"> Output parameter receiving the longitude in degrees. </param>
public static void PixelXYToLatLong( int pixelX, int pixelY, int levelOfDetail, out double latitude, out double longitude)
{
double mapSize = MapSize(levelOfDetail);
double x = (Clip(pixelX, 0 , mapSize - 1 ) / mapSize) - 0.5 ;
double y = 0.5 - (Clip(pixelY, 0 , mapSize - 1 ) / mapSize);
latitude = 90 - 360 * Math.Atan(Math.Exp( - y * 2 * Math.PI)) / Math.PI;
longitude = 360 * x;
}
/// <summary>
/// Converts pixel XY coordinates into tile XY coordinates of the tile containing
/// the specified pixel.
/// </summary>
/// <param name="pixelX"> Pixel X coordinate. </param>
/// <param name="pixelY"> Pixel Y coordinate. </param>
/// <param name="tileX"> Output parameter receiving the tile X coordinate. </param>
/// <param name="tileY"> Output parameter receiving the tile Y coordinate. </param>
public static void PixelXYToTileXY( int pixelX, int pixelY, out int tileX, out int tileY)
{
tileX = pixelX / 256 ;
tileY = pixelY / 256 ;
}
/// <summary>
/// Converts tile XY coordinates into pixel XY coordinates of the upper-left pixel
/// of the specified tile.
/// </summary>
/// <param name="tileX"> Tile X coordinate. </param>
/// <param name="tileY"> Tile Y coordinate. </param>
/// <param name="pixelX"> Output parameter receiving the pixel X coordinate. </param>
/// <param name="pixelY"> Output parameter receiving the pixel Y coordinate. </param>
public static void TileXYToPixelXY( int tileX, int tileY, out int pixelX, out int pixelY)
{
pixelX = tileX * 256 ;
pixelY = tileY * 256 ;
}
/// <summary>
/// Converts tile XY coordinates into a QuadKey at a specified level of detail.
/// </summary>
/// <param name="tileX"> Tile X coordinate. </param>
/// <param name="tileY"> Tile Y coordinate. </param>
/// <param name="levelOfDetail"> Level of detail, from 1 (lowest detail)
/// to 23 (highest detail). </param>
/// <returns> A string containing the QuadKey. </returns>
public static string TileXYToQuadKey( int tileX, int tileY, int levelOfDetail)
{
StringBuilder quadKey = new StringBuilder();
for ( int i = levelOfDetail; i > 0 ; i -- )
{
char digit = ' 0 ' ;
int mask = 1 << (i - 1 );
if ((tileX & mask) != 0 )
{
digit ++ ;
}
if ((tileY & mask) != 0 )
{
digit ++ ;
digit ++ ;
}
quadKey.Append(digit);
}
return quadKey.ToString();
}
/// <summary>
/// Converts a QuadKey into tile XY coordinates.
/// </summary>
/// <param name="quadKey"> QuadKey of the tile. </param>
/// <param name="tileX"> Output parameter receiving the tile X coordinate. </param>
/// <param name="tileY"> Output parameter receiving the tile Y coordinate. </param>
/// <param name="levelOfDetail"> Output parameter receiving the level of detail. </param>
public static void QuadKeyToTileXY( string quadKey, out int tileX, out int tileY, out int levelOfDetail)
{
tileX = tileY = 0 ;
levelOfDetail = quadKey.Length;
for ( int i = levelOfDetail; i > 0 ; i -- )
{
int mask = 1 << (i - 1 );
switch (quadKey[levelOfDetail - i])
{
case ' 0 ' :
break ;
case ' 1 ' :
tileX |= mask;
break ;
case ' 2 ' :
tileY |= mask;
break ;
case ' 3 ' :
tileX |= mask;
tileY |= mask;
break ;
default :
throw new ArgumentException( " Invalid QuadKey digit sequence. " );
}
}
}
}
}
注:本文中内容来源于互联网整理而成,如涉及到任何侵权等行为请联系本人。
推荐资源:
转载自http://www.cnblogs.com/beniao/archive/2010/04/18/1714544.html
