【常见缓存算法原理及其C++实现】LRU篇（包含过期时间详解）
一、缓存算法简介
（一）缓存算法应用背景
缓存的应用场景和范围十分广泛，下面给出其十分常见的两种应用背景：
首先，在操作系统内部，由于内存资源十分有限，而每个进程又都希望独享一块很大的内存空间。所以诞生了一种“虚拟内存”机制，它将进程的一部分内容暂留在磁盘中，在需要时再进行数据交换将其放入内存，这个过程就需要用到缓存算法机制进行置换。
其次，对于各类应用项目开发而言，在巨大的数据量面前，Cache 是不可或缺的。因为无论是针对本地端的浏览器缓存，还是针对服务器端的缓存(例如，redis 内存数据库缓存)，Cache 都是提高性能的最常用的一种方式。它不仅可以加速用户的访问，同时也可以降低服务器的负载和压力。
（二）常见缓存算法原理
1、FIFO（Fist In First Out）
先进先出，这是最简单、最公平的一种算法，它认为一个数据最早进入缓存，在将来该数据被访问的可能性最小。其原理是最早进入缓存的数据应该最早被淘汰掉，即当缓存空间被占满时，最先进入的数据会被最早被淘汰。
2、LRU（Least Recently Used）
最近最少使用，它的设计原则借鉴了时间局部性原理，该算法认为如果数据最近被访问过，那么将来被访问的几率也更高，反之亦然。其原理是将数据按照其被访问的时间形成一个有序序列，最久未被使用的数据应该最早被淘汰掉，即当缓存空间被占满时，缓存内最长时间未被使用的数据将被淘汰掉。
3、LFU（Least Frequently Used）
最不经常使用，它的设计原则使用了概率思想，该算法认为如果一个对象的被访问频率很低，那么再次被访问的概率也越低。其原理是缓存空间中被访问次数最少的数据应该最早被淘汰掉，即当缓存空间被占满时，缓存内被访问频率最少的数据将被置换走。
详细原理及C++实现可参考我的另一篇博客，应对面试这一篇就够了 LFU详解及C++实现
二、LRU 基本算法描述
- 初始化一个大小为 n 的缓存空间，结构如上图所示，缓存中的数据为
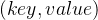结构； - 当有新加入数据操作时，先判断该 key 值是否已经在缓存空间中，如果在的话更新 key 对应的 value 值，并把该数据加入到缓存空间的最右边；
- 如果新加入数据的 key 值不在缓存空间中，则判断缓存空间是否已满，若缓存空间未满，则构造新的节点加入到缓存空间的最右边，否则把该数据加入到缓存空间的右边并淘汰掉队列最左边的数据（缓存中最久未被使用的数据）；
- 访问一个数据且该数据存在于缓存空间中，返回该数据对应值并将该数据放入缓存空间的最右边；
- 访问一个数据但该数据不存在于缓存空间中，返回 - 1 表示缓存中无该数据。
上述仅仅是 LRU 算法的一个最基本的过程，可以看出主要设计到加入数据及访问数据两个操作，在实际应用场景中，我们希望这两个操作的平均时间复杂度均可以控制在 O(1) 内，以保证缓存的高效运行，具体实现方法及策略在下节中会给出。
三、LRU 算法实现
（一）基本 LRU 算法实现
1、基本 LRU 算法主要函数及数据结构
-
：缓存空间初始化，以 正整数 capacity 作为容量初始化 LRU 缓存。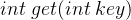 
：访问缓存数据，如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
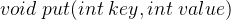：向缓存中加入数据，如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。
算法实现过程中的难点在于要在 O(1) 的时间复杂度下完成 get 和 put 两个操作，所以好的数据结构的选择至关重要，首先我们先来总结一下 LRUCache 这个数据结构必要的条件：
- 显然 LRUC
ache中的元素必须有时序，以区分最近使用的和久未使用的数据。当容量满了之后要淘汰最久未使用的数据以供新元素使用；put 操作需要将数据作为最近使用的元素加入 LRUCache 中。 - get 操作需要在 LRUC
ache中快速定位某个 key 是否已存在并返回其对应的 val，且每次访问 该 key，需要将这个元素变为最近使用的，即 LRUCache要支持在任意位置快速插入和删除元素。
思考一下什么数据结构能满足上述条件呢？哈希表可以快速定位与查找，但是不能够满足时序这个条件；双向链表可以满足时序条件，并且可以同时操作最近使用和最久未使用的两个边界元素，但是不能在 O(1) 时间复杂度内完成定位工作。故结合一下二者，采用双向链表及哈希表结合的方式来实现即可，具体 LRUCache 结构如下图所示。
2、基本 LRU 算法代码
（1）首先，我们先来定义一下双向链表中的节点结构 Node
//双向链表节点，采用kv键值对形式
struct Node{
int key;
int value;
Node *pre,*next;//双向链表的前驱和后继指针
Node(int k,int v)//构造函数
{
key=k;
value=v;
pre=nullptr;
next=nullptr;
}
};（2）然后，我们再定义一下 LRUCache 中的哈希表结构 hash 、缓存容量 n 、双向链表的哨兵节点表头 L（最久未被使用）及表尾 R（最近使用），其中哨兵节点用于防止操作过程中内存溢出
int n;//缓存容量
//哈希表，哈希表的 结构是为了方便与双向链表进行交互
unordered_map hash;
//双向链表哨兵节点
Node *L,*R;
（3）下面，来实现一下缓存空间初始化函数
//缓存空间初始化函数
LRUCache(int capacity) {
n=capacity;//初始化空间大小 n 为 capacity
//为哨兵节点分配内存空间
L=new Node(-1,-1);
R=new Node(-1,-1);
//完成哨兵节点的链接
L->next=R;
R->pre=L;
}（4）再来实现一下访问缓存数据的 get 函数
//访问缓存数据函数
int get(int key) {
if(hash.find(key)!=hash.end())//缓存中存在该 key
{
Node *node=hash[key];//从 hash 表中以 O(1) 速度取出 Node * 结构数据
//下面完成的是删除双向链表及 hash 中原有的点，并将该节点加入最近使用的表尾 R 的前驱操作
remove(node);
insert(node->key,node->value);
return node->value;//返回 key 对应的 val
}
else return -1;//缓存中不存在该 key
}（5）再来实现一下更新缓存数据的 put 函数
//更新缓存数据函数
void put(int key, int value) {
if(hash.find(key)!=hash.end())//缓存中存在该 key
{
Node *node=hash[key];//从 hash 表中以 O(1) 速度取出 Node * 结构数据
//下面完成的是删除双向链表及 hash 中原有的点，并将该节点更新 value 值后加入最近使用的表尾 R 的前驱操作
remove(node);
insert(key,value);
}
// if(get(key)!=-1)
// hash[key]->val=value;
else//缓存中不存在该 key
{
if(hash.size()==n)//缓存已满
{
//删除双向链表表头 L 指向的节点
Node *node=L->next;
remove(node);
//新节加入最近使用的表尾 R 的前驱操作
insert(key,value);
}
else insert(key,value);//缓存未满，直接插入
}
}（6）get 和 put 函数涉及到两个新的函数 remove 和 insert，分别用于移除和插入双向链表和哈希表中的对应节点数据，下面实现一下这两个函数
//删除双向链表及 hash 中的点
void remove(Node *node)
{
//双向链表中 node 前驱指向后继，后继指向前驱，消灭 node
Node *pre=node->pre;
Node *next=node->next;
pre->next=next;
next->pre=pre;
//哈希表删除 node
hash.erase(node->key);
//释放 node 指向的内存资源
delete node;
node=nullptr;
}
//更新双向链表及 hash 中的点
void insert(int key,int value)
{
//双向链表中表尾 R 的前驱对应的是最近使用的节点
Node *pre=R->pre;
Node *next=R;
//构造新节点，插入双向链表（前驱后继两个方向的指针都要修改）
Node *newNode=new Node(key,value);
//后继方向right ->
pre->next=newNode;
newNode->next=next;
//前驱方向left <-
next->pre=newNode;
newNode->pre=pre;
//哈希表更新 node
hash[key]=newNode;
}（7）完整代码及注释如下，以供大家参考，完成上述内容学习，顺便大家还可以解决一下 LeetCode 146 题
class LRUCache {
private:
//双向链表节点，采用kv键值对形式
struct Node{
int key;
int value;
Node *pre,*next;//双向链表的前驱和后继指针
Node(int k,int v)//构造函数
{
key=k;
value=v;
pre=nullptr;
next=nullptr;
}
};
int n;//缓存容量
//哈希表，哈希表的 结构是为了方便与双向链表进行交互
unordered_map hash;
//双向链表哨兵节点
Node *L,*R;
//删除双向链表及 hash 中的点
void remove(Node *node)
{
//双向链表中 node 前驱指向后继，后继指向前驱，消灭 node
Node *pre=node->pre;
Node *next=node->next;
pre->next=next;
next->pre=pre;
//哈希表删除 node
hash.erase(node->key);
//释放 node 指向的内存资源
delete node;
node=nullptr;
}
//更新双向链表及 hash 中的点
void insert(int key,int value)
{
//双向链表中表尾 R 的前驱对应的是最近使用的节点
Node *pre=R->pre;
Node *next=R;
//构造新节点，插入双向链表（前驱后继两个方向的指针都要修改）
Node *newNode=new Node(key,value);
//后继方向right ->
pre->next=newNode;
newNode->next=next;
//前驱方向left <-
next->pre=newNode;
newNode->pre=pre;
//哈希表更新 node
hash[key]=newNode;
}
public:
//缓存空间初始化函数
LRUCache(int capacity) {
n=capacity;//初始化空间大小 n 为 capacity
//为哨兵节点分配内存空间
L=new Node(-1,-1);
R=new Node(-1,-1);
//完成哨兵节点的链接
L->next=R;
R->pre=L;
}
//访问缓存数据函数
int get(int key) {
if(hash.find(key)!=hash.end())//缓存中存在该 key
{
Node *node=hash[key];//从 hash 表中以 O(1) 速度取出 Node * 结构数据
//下面完成的是删除双向链表及 hash 中原有的点，并将该节点加入最近使用的表尾 R 的前驱操作
remove(node);
insert(node->key,node->value);
return node->value;//返回 key 对应的 val
}
else return -1;//缓存中不存在该 key
}
//更新缓存数据函数
void put(int key, int value) {
if(hash.find(key)!=hash.end())//缓存中存在该 key
{
Node *node=hash[key];//从 hash 表中以 O(1) 速度取出 Node * 结构数据
//下面完成的是删除双向链表及 hash 中原有的点，并将该节点更新 value 值后加入最近使用的表尾 R 的前驱操作
remove(node);
insert(key,value);
}
// if(get(key)!=-1)
// hash[key]->val=value;
else//缓存中不存在该 key
{
if(hash.size()==n)//缓存已满
{
//删除双向链表表头 L 指向的节点
Node *node=L->next;
remove(node);
//新节加入最近使用的表尾 R 的前驱操作
insert(key,value);
}
else insert(key,value);//缓存未满，直接插入
}
}
}; （二）定时过期的 LRU 算法实现
1、定时过期的 LRU 算法主要函数及数据结构
带定时过期机制的 LRU 和基本 LRU 情况略有不同，主要体现在以下两个函数中：
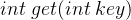- ：访问缓存数据，如果关键字 key 存在于缓存中，先检查该数据是否已经过期，若未过期，则重新设置该数据的过期时间，后返回关键字的值，若已过期返回 -1 ；如果关键字 key 不存在于缓存中，则返回 -1。
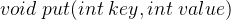- ：向缓存中加入数据，如果关键字 key 已经存在，则变更其数据值 value，同时重新设置该数据的过期时间；如果不存在，则向缓存中插入该组 key-value 并设置其过期时间。如果插入操作导致关键字数量超过 capacity ，则应该先检查缓存中是否存在已过期的数据，如果存在选择任意一条过期数据淘汰，否则逐出最久未使用的关键字。（注意：这里的逻辑是符合常理的，但是可以简化为不论当前缓存中是否存在过期数据均逐出最久未使用的关键字，因为定时过期意味着最先插入的元素一定是最先过期的，那么当缓存已满的条件下，不论其是否真正过期，均可以直接逐出缓存）
定时过期机制的引入并未改变算法主要数据结构的选择，依然采用双向链表和哈希表来实现该算法；也可以在O(1) 的时间复杂度下完成 get 和 put 两个操作。
事实上，它的原理几乎基本 LRU 一模一样，只是加入了过期时间这样一个变量，本文之所以引入定时过期的 LRU 算法，是为后文不定时过期的 LRU 算法做铺垫。
2、定时过期的 LRU 算法代码
下仅针对基本 LRU 算法改动部分进行详解。
（1）首先，双向链表中的节点结构 Node 需要增加一个 expireTime 数据，以记录该节点的过期时间，它的数据类型选择 time.h 头文件中的 time_t
struct Node{
int key;
int value;
time_t expireTime;
Node *pre,*next;
Node(int key,int value,time_t expireTime)//expireTime 以秒为单位
{
this->key=key;
this->value=value;
this->expireTime=expireTime;
pre=nullptr;
next=nullptr;
}
};（2）其次，需要定义一个全局变量，用于标记定时过期机制中的固定过期时间间隔
const int ttl=5;//存活时间（过期时间间隔）（3）然后，再来修改一下访问缓存数据的 get 函数，这里采用 time.h 头文件中的 time 函数来获取系统当前时间 curTime，后利用 difftime 函数比较节点过期时间与系统当前时间的大小，以进行过期与否判断
int get(int key)
{
if(hash.find(key)!=hash.end())
{
Node *node=hash[key];
//在访问时就判断该数据是否过期
//取系统当前时间
time_t curTime;
curTime=time(nullptr);
//判断是否过期
if(difftime(node->expireTime,curTime)<=0)//过期返回 -1
{
remove(node);
return -1;
}
else//未过期，重新设置该数据的过期时间
{
remove(node);
insert(node->key,node->value);
return node->value;
}
}
else return -1;
}（4）再来修改一下更新缓存数据的 put 函数，同样加上了过期判断
void put(int key,int value)
{
if(hash.find(key)!=hash.end())
{
Node *node=hash[key];
remove(node);
insert(key,value);
}
else
{
if(hash.size()==n)//缓存满
{
//无论是否存在过期节点，淘汰双向链表的表头 L 的后继节点
Node *node=L->next;
remove(node);
insert(key,value);
}
else insert(key,value);
}
}（5）最后，get 和 put 中涉及的 insert 函数也有所改动，其中 ttl 即是定时过期机制中的固定过期时间间隔
void insert(int key,int value)
{
time_t curTime;
curTime=time(nullptr);
Node *newNode=new Node(key,value,curTime+ttl);//每次重新插入均重置超时时间为 curTime + ttl
Node *pre=R->pre;
Node *next=R;
pre->next=newNode;
newNode->next=next;
next->pre=newNode;
newNode->pre=pre;
hash[key]=newNode;
}（6）下面给出完整代码以供参考
/*含过期时间机制（过期间隔相同）的LRU-begin*/
const int ttl=5;//存活时间（过期时间间隔）
class LRUWithTTL{
private:
struct Node{
int key;
int value;
time_t expireTime;
Node *pre,*next;
Node(int key,int value,time_t expireTime)//expireTime 以秒为单位
{
this->key=key;
this->value=value;
this->expireTime=expireTime;
pre=nullptr;
next=nullptr;
}
};
int n;
unordered_map hash;
Node *L,*R;
void remove(Node *node)
{
Node *pre=node->pre;
Node *next=node->next;
pre->next=next;
next->pre=pre;
hash.erase(node->key);
//释放 node 指向的内存资源
delete node;
node=nullptr;
}
void insert(int key,int value)
{
time_t curTime;
curTime=time(nullptr);
Node *newNode=new Node(key,value,curTime+ttl);//每次重新插入均重置超时时间为 curTime + ttl
Node *pre=R->pre;
Node *next=R;
pre->next=newNode;
newNode->next=next;
next->pre=newNode;
newNode->pre=pre;
hash[key]=newNode;
}
public:
LRUWithTTL(int capacity)
{
n=capacity;
L=new Node(-1,-1,0);
R=new Node(-1,-1,0);
L->next=R;
R->pre=L;
}
int get(int key)
{
if(hash.find(key)!=hash.end())
{
Node *node=hash[key];
//在访问时就判断该数据是否过期
//取系统当前时间
time_t curTime;
curTime=time(nullptr);
//判断是否过期
if(difftime(node->expireTime,curTime)<=0)//过期返回 -1
{
remove(node);
return -1;
}
else//未过期，重新设置该数据的过期时间
{
remove(node);
insert(node->key,node->value);
return node->value;
}
}
else return -1;
}
void put(int key,int value)
{
if(hash.find(key)!=hash.end())
{
Node *node=hash[key];
remove(node);
insert(key,value);
}
else
{
if(hash.size()==n)//缓存满
{
//取系统当前时间
time_t curTime;
curTime=time(nullptr);
bool isExpire=false;//标记是否有过期节点
//遍历哈希表试图寻找第一个过期的 Node
unordered_map::iterator it;
for(it=hash.begin();it!=hash.end();++it)
{
if(difftime(it->second->expireTime,curTime)<=0)
{
isExpire=true;
break;
}
}
if(isExpire)//有过期节点，淘汰过期节点
{
remove(it->second);
insert(key,value);
}
else//没有过期节点，淘汰双向链表的表头 L 的后继节点
{
Node *node=L->next;
remove(node);
insert(key,value);
}
}
else insert(key,value);
}
}
};
/*含过期时间机制（过期间隔相同）的LRU-end*/ （三）不定时过期的 LRU 算法实现
1、不定时过期的 LRU 算法主要函数及数据结构
不定时过期与定时过期的唯一差别就在于过期时间间隔 ttl 的操作上，这个差别涉及到get 及 put 函数：
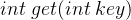- ：访问缓存数据，如果关键字 key 存在于缓存中，先检查该数据是否已经过期，若未过期，则重新插入该数据时保持其过期时间不变，后返回关键字的值，若已过期返回 -1 ；如果关键字 key 不存在于缓存中，则返回 -1。
-
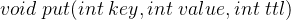：向缓存中加入数据，如果关键字 key 已经存在，则变更其数据值 value，同时重新设置该数据的过期时间间隔 ttl；如果不存在，则向缓存中插入该组 key-value 并设置其过期时间间隔 ttl。如果插入操作导致关键字数量超过 capacity ，则应该先检查缓存中是否存在已过期的数据，如果存在选择任意一条过期数据淘汰，否则逐出最久未使用的关键字。
同样，不定时过期机制的引入并未改变算法主要数据结构的选择，依然采用双向链表和哈希表来实现该算法。该算法可以在O(1) 的时间复杂度下完成 get 操作，但是 put 操作的时间复杂度变为了O(n)。
2、不定时过期的 LRU 算法代码
下仅针对定时过期的 LRU 算法改动部分进行详解。
（1）get 函数的修改
int get(int key)
{
if(hash.find(key)!=hash.end())
{
Node *node=hash[key];
time_t curTime;
curTime=time(nullptr);
if(difftime(node->expireTime,curTime)<=0)
{
remove(node);
return -1;
}
else
{
remove(node);
//保持该节点过期时间不变
int timeLeft=difftime(node->expireTime,curTime);
insert(node->key,node->value,timeLeft);
return node->value;
}
}
else return -1;
}（2）put 函数的修改
//每次更新新节点需要显式加上其存活时间 ttl（每个节点 ttl 可不同）
void put(int key,int value,int ttl)
{
if(hash.find(key)!=hash.end())
{
Node *node=hash[key];
remove(node);
insert(key,value,ttl);//加 ttl
}
else
{
if(hash.size()==n)
{
time_t curTime;
curTime=time(nullptr);
unordered_map::iterator it;
bool isExpire=false;
for(it=hash.begin();it!=hash.end();++it)
{
if(difftime(it->second->expireTime,curTime)<=0)
{
isExpire=true;
break;
}
}
if(isExpire)
{
remove(it->second);
insert(key,value,ttl);//加 ttl
}
else
{
Node *node=L->next;
remove(node);
insert(key,value,ttl);//加 ttl
}
}
else insert(key,value,ttl);//加 ttl
}
} （3）完整代码如下以供参考
/*含过期时间机制（过期间隔不同，自行指定）的LRU-begin*/
class LRUWithDiffTTL{
private:
struct Node{
int key;
int value;
time_t expireTime;
Node *pre,*next;
Node(int key,int value,time_t expireTime)//expireTime 以秒为单位
{
this->key=key;
this->value=value;
this->expireTime=expireTime;
pre=nullptr;
next=nullptr;
}
};
int n;
unordered_map hash;
Node *L,*R;
void remove(Node *node)
{
Node *pre=node->pre;
Node *next=node->next;
pre->next=next;
next->pre=pre;
hash.erase(node->key);
//释放 node 指向的内存资源
delete node;
node=nullptr;
}
//每次插入新节点需要加上其存活时间 ttl（每个节点 ttl 可不同）
void insert(int key,int value,int ttl)
{
time_t curTime;
curTime=time(nullptr);
Node *newNode=new Node(key,value,curTime+ttl);
Node *pre=R->pre;
Node *next=R;
pre->next=newNode;
newNode->next=next;
next->pre=newNode;
newNode->pre=pre;
hash[key]=newNode;
}
public:
LRUWithDiffTTL(int capacity)
{
n=capacity;
L=new Node(-1,-1,0);
R=new Node(-1,-1,0);
L->next=R;
R->pre=L;
}
int get(int key)
{
if(hash.find(key)!=hash.end())
{
Node *node=hash[key];
time_t curTime;
curTime=time(nullptr);
if(difftime(node->expireTime,curTime)<=0)
{
remove(node);
return -1;
}
else
{
remove(node);
//保持该节点过期时间不变
int timeLeft=difftime(node->expireTime,curTime);
insert(node->key,node->value,timeLeft);
return node->value;
}
}
else return -1;
}
//每次更新新节点需要显式加上其存活时间 ttl（每个节点 ttl 可不同）
void put(int key,int value,int ttl)
{
if(hash.find(key)!=hash.end())
{
Node *node=hash[key];
remove(node);
insert(key,value,ttl);//加 ttl
}
else
{
if(hash.size()==n)
{
time_t curTime;
curTime=time(nullptr);
unordered_map::iterator it;
bool isExpire=false;
for(it=hash.begin();it!=hash.end();++it)
{
if(difftime(it->second->expireTime,curTime)<=0)
{
isExpire=true;
break;
}
}
if(isExpire)
{
remove(it->second);
insert(key,value,ttl);//加 ttl
}
else
{
Node *node=L->next;
remove(node);
insert(key,value,ttl);//加 ttl
}
}
else insert(key,value,ttl);//加 ttl
}
}
};
/*含过期时间机制（过期间隔不同-自行指定）的LRU-end*/ 补充：针对有过期机制的 LRU 算法进行测试时，需借助睡眠函数进行辅助操作，不同的操作系统睡眠函数的使用方法有所不同，具体情况如下表
| 操作系统 | 头文件 | 函数形式 | 时间单位 |
|---|---|---|---|
| Linux/MacOS | #include |
unsigned int sleep(unsigned int) | 秒 |
| Windows | #include |
void Sleep(DWORD) | 毫秒 |