设计一个灵活的Camera类设计
D3DXMatrixLookAtLH函数可计算出观察矩阵(取景变换矩阵),当在某一固定点固定摄像机方位时,该函数十分有用,但其用户接口对于一个能够根据用户输入做出响应移动的摄像机来说,就会力不从心。我们可以实现一个Camera类以使我们能够较D3DXMatrixLookAtLH函数对摄像机更好的控制,该类特别适合于飞行模拟器、第一人称视角游戏。
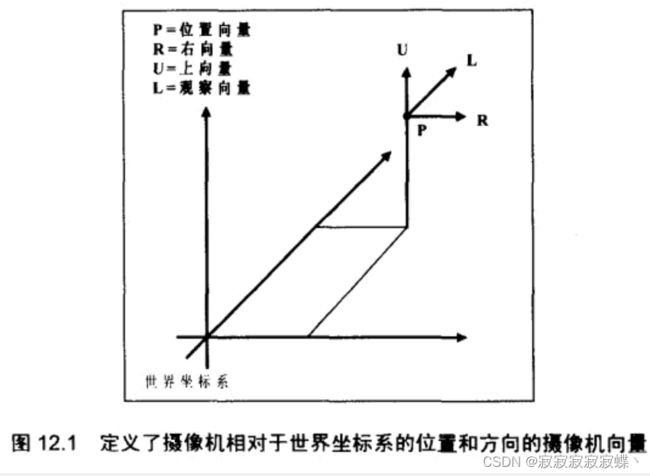
摄像机的4个向量:右向量、上向量、观察向量、位置向量
通过这些向量来定义摄像机相对于世界坐标系的位置和朝向,前3个向量统称为方向向量,方向向量必须是标准正交的(如果一个向量集中的向量都彼此正交,且模为1,则称该向量是标准正交的)。引入这个约束的原因是后面需要将这些向量插入到一个矩阵的某些行中,以使该矩阵成为标准正交矩阵(如果一个矩阵的行向量是标准正交的),标准正交矩阵的一个重要性质是其逆矩阵与其转置矩阵相等。
摄像机的6中变换运算
- 绕向量right的旋转(俯仰,pitch)
- 绕向量up的旋转(偏航,yaw)
- 绕向量look的旋转(滚动,roll)
- 沿向量right方向的扫视(strafe)
- 沿向量up方向的升降(fly)
- 沿向量look的平动
//灵活camera
class Camera
{
public:
enum CameraType
{
LANDOBJECT, //摄像机沿某些特定轴进行移动
AIRCRAFT //摄像机自由移动
};
Camera();
Camera(CameraType cameraType);
~Camera();
void Strafe(float units);
void Fly(float units);
void Walk(float units);
void Pitch(float angle);
void Yaw(float angle);
void Roll(float angle);
void GetViewMatrix(D3DXMATRIX* v);
void SetCameraType(CameraType cameraType);
void GetPosition(D3DXVECTOR3* pos);
void SetPosition(D3DXVECTOR3* pos);
void GetRight(D3DXVECTOR3* right);
void GetUp(D3DXVECTOR3* up);
void GetLook(D3DXVECTOR3* look);
private:
CameraType m_cameraType;
D3DXVECTOR3* m_right;
D3DXVECTOR3* m_up;
D3DXVECTOR3* m_look;
D3DXVECTOR3* m_pos;
};观察矩阵(取景变换)的计算
position向量:![]()
right向量:![]()
up向量:![]()
look向量:![]()
取景变换所解决的问题其实就是世界坐标系中的物体在以摄像机为中心的坐标系中如果进行描述,等价于将世界坐标系中的物体随摄像机一起进行变换,以使摄像机坐标系与世界坐标系完全重合。所以希望变换矩阵V能够实现:
- pV=(0,0,0) 矩阵V将摄像机移至世界坐标系原点
- rV=(1,0,0) 矩阵V将摄像机的right向量与世界坐标系的x轴重合
- uV=(0,1,0) 矩阵V将摄像机的up向量与世界坐标系的y轴重合
- dV=(0,0,1) 矩阵v将摄像机的look向量与世界坐标系的z轴重合
1.平移
2.旋转,我们需要一个3x3的旋转矩阵A以使3个向量与世界坐标系的x,y,z轴重合,该矩阵需要满足以下方程
这里使用是3x3矩阵,因为不需要用齐次坐标来表示旋转,后面再将其扩展为4x4矩阵,由以上方程可建立新的方程为
矩阵A有多种求解方式,但可以立即看出A其实是B的逆矩阵(![]() ),由于矩阵B是标准正交矩阵(行向量构成了一组标准正交基),所以其逆矩阵与其转置矩阵相等。
),由于矩阵B是标准正交矩阵(行向量构成了一组标准正交基),所以其逆矩阵与其转置矩阵相等。
3.整合前两步,将A扩展为4x4矩阵后与平移矩阵整合,得到观察矩阵V
函数前面几行的意思是,在几次旋转变换后由于浮点数的误差,摄像机的各向量可能不再是标准正交的,所以每次调用该函数时必须重新根据向量look计算up、right来保证三者相互正交,新的正交向量up可由up=look x right得到,新的正交向量right可由right=up x look计算得到。
void d3d::Camera::GetViewMatrix(D3DXMATRIX* v)
{
D3DXVec3Normalize(&m_look, &m_look);
D3DXVec3Cross(&m_up, &m_look, &m_right);
D3DXVec3Normalize(&m_up, &m_up);
D3DXVec3Cross(&m_right, &m_up, &m_look);
D3DXVec3Normalize(&m_right, &m_right);
//构建取景矩阵
float x = -D3DXVec3Dot(&m_right, &m_pos);
float y = -D3DXVec3Dot(&m_up, &m_pos);
float z = -D3DXVec3Dot(&m_look, &m_pos);
(*v)(0, 0) = m_right.x;
(*v)(0, 1) = m_up.x;
(*v)(0, 2) = m_look.x;
(*v)(0, 3) = 0.0f;
(*v)(1, 0) = m_right.y;
(*v)(1, 1) = m_up.y;
(*v)(1, 2) = m_look.y;
(*v)(1, 3) = 0.0f;
(*v)(2, 0) = m_right.z;
(*v)(2, 1) = m_up.z;
(*v)(2, 2) = m_look.z;
(*v)(2, 3) = 0.0f;
(*v)(3, 0) = x;
(*v)(3, 1) = y;
(*v)(3, 2) = z;
(*v)(3, 3) = 1.0f;
}绕任意轴的旋转
D3DX库提供了D3DXMatrixRotationAxis函数来支持绕任意轴进行旋转
D3DXMATRIX* D3DXMatrixRotationAxis(
D3DXMATRIX *pOut,
CONST D3DXVECTOR3 *pV,
FLOAT Angle
);
D3DXMATRIX R;
D3DXVECTOR3 axis(0.707f, 0.707f, 0.0f);
D3DXMatrixRotationAxis(&R, &axis, D3DX_PI / 2.0f);俯仰、偏航、滚动
LANDOBJECT类型摄像机需要增加一些约束,尤其是当一个地面物体俯仰之后又发生了偏航或滚动,这样看起来会有问题。所以对于LANDOBJECT类型的摄像机,应使其绕世界坐标系的y轴旋转而非yaw中的up向量,而且应该完全禁止地面物体发生滚动。
void d3d::Camera::Pitch(float angle)
{
//俯仰
D3DXMATRIX T;
D3DXMatrixRotationAxis(&T, &m_right, angle);
D3DXVec3TransformCoord(&m_up, &m_up, &T);
D3DXVec3TransformCoord(&m_look, &m_look, &T);
}
void d3d::Camera::Yaw(float angle)
{
//偏航
D3DXMATRIX T;
if (m_cameraType == LANDOBJECT)
D3DXMatrixRotationY(&T, angle);
else if (m_cameraType == AIRCRAFT)
D3DXMatrixRotationAxis(&T, &m_up, angle);
D3DXVec3TransformCoord(&m_right, &m_right, &T);
D3DXVec3TransformCoord(&m_look, &m_look, &T);
}
void d3d::Camera::Roll(float angle)
{
//滚动
if (m_cameraType == AIRCRAFT)
{
D3DXMATRIX T;
D3DXMatrixRotationAxis(&T, &m_look, angle);
D3DXVec3TransformCoord(&m_right, &m_right, &T);
D3DXVec3TransformCoord(&m_up, &m_up, &T);
}
}行走、扫视、升降
地面物体的运动也要增加一些约束,LANDOBJECT类型摄像机不应在观察方向朝上时沿着up向量升降或平动,也不应该在一个斜面上进行扫视,需要把摄像机的行动限制在xz平面上,由于LANDOBJECT可以改变其高度(爬山、爬楼梯),所以专门提供了SetPosition方法可使手工将摄像机指定在一个合适的高度和位置上。
void d3d::Camera::Strafe(float units)
{
//扫视
if (m_cameraType == LANDOBJECT)
m_pos += D3DXVECTOR3(m_look.x, 0.0f, m_look.z) * units;
else if (m_cameraType == AIRCRAFT)
m_pos += m_right * units;
}
void d3d::Camera::Fly(float units)
{
//升降
if (m_cameraType == LANDOBJECT)
m_pos.y += units;
else if (m_cameraType == AIRCRAFT)
m_pos += m_up * units;
}
void d3d::Camera::Walk(float units)
{
//行走
if (m_cameraType == LANDOBJECT)
m_pos += D3DXVECTOR3(m_look.x, 0.0f, m_look.z) * units;
else if (m_cameraType == AIRCRAFT)
m_pos += m_look * units;
}
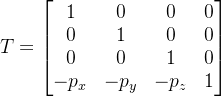
![rA=[r_{x},r_{y},r_{z}]\begin{bmatrix} a_{00} & a_{01} &a_{02} \\ a_{10} & a_{11} & a_{12}\\ a_{20} & a_{21} & a_{22} \end{bmatrix}=[1,0,0]](http://img.e-com-net.com/image/info8/44e618bed7114536a2fc1484ef513a4d.png)
![uA=[u_{x},u_{y},u_{z}]\begin{bmatrix} a_{00} & a_{01} &a_{02} \\ a_{10} & a_{11} & a_{12}\\ a_{20} & a_{21} & a_{22} \end{bmatrix}=[0,1,0]](http://img.e-com-net.com/image/info8/ae040ad0cefb4fc3aa78cf160cb0eb0f.png)
![dA=[d_{x},d_{y},d_{z}]\begin{bmatrix} a_{00} & a_{01} &a_{02} \\ a_{10} & a_{11} & a_{12}\\ a_{20} & a_{21} & a_{22} \end{bmatrix}=[0,0,1]](http://img.e-com-net.com/image/info8/8e396215845d4ef4bf93ee46c785409e.png)
