代码随想录Day17 LeetCode T98 验证二叉搜索树 T530 二叉搜索树的最小绝对差 T501 二叉搜索树中的众数 T236二叉搜索树的最近公共祖先

本文详细思路来自于:代码随想录 (programmercarl.com)

前言

二叉搜索树的中序遍历

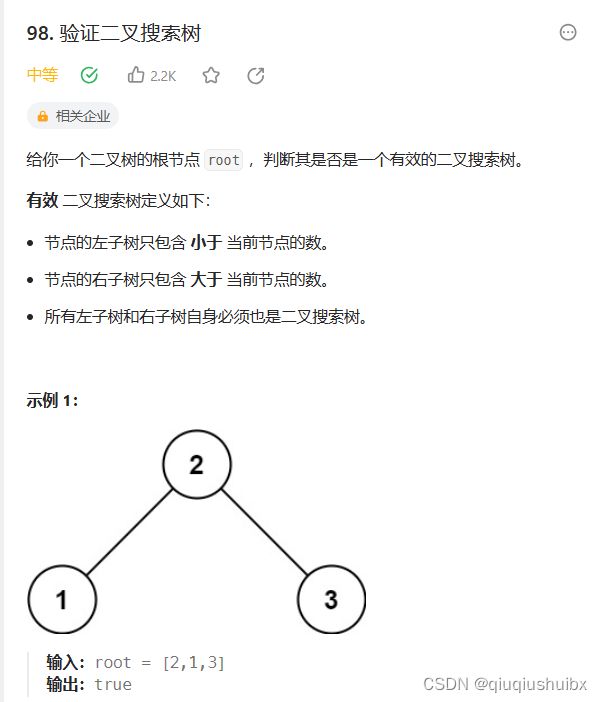
LeetCode T98 验证二叉搜索树

题目链接:力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

 

题目思路:

这题我们仍然采用递归的思路解答,我们知道二叉搜索树的特征是,根节点比左子树来的大,跟根节点比右子树来的小,这样我们就有一个很直白的思路,如果我们使用中序遍历,这样我们遍历的二叉树就是递增的,我们可以给一个result = Long.MAX_VALUE,按照这个遍历方式来比较,每次更新,但是我们知道,肯定有比long类型更大的数字的,有没有更好的解决方式呢?

这里我们还是可以采用双指针的思路,一个指针指向前一个节点,一个指针指向后一个节点,两个节点做比较即可.

1.确定参数:这里已经定义好了参数,无需修改,直接操作即可.

2.确定终止条件

    if(root == null)
        {
            return true;
        }
//注意:空树是满足要求的

3.确定一次递归条件(中序遍历)

        boolean left = isValidBST(root.left);
        
        if(pre!=null && pre.val>=root.val)//第一次是不会进来的
        {
            return false;
        }
        pre = root;
        boolean right = isValidBST(root.right);
        return right && left;

题目代码:

class Solution {
    TreeNode pre = null;
    public boolean isValidBST(TreeNode root) {
        if(root == null)
        {
            return true;
        }
        //左
        boolean left = isValidBST(root.left);
        
        if(pre!=null && pre.val>=root.val)
        {
            return false;
        }
        pre = root;
        boolean right = isValidBST(root.right);
        return right && left;
    }
}

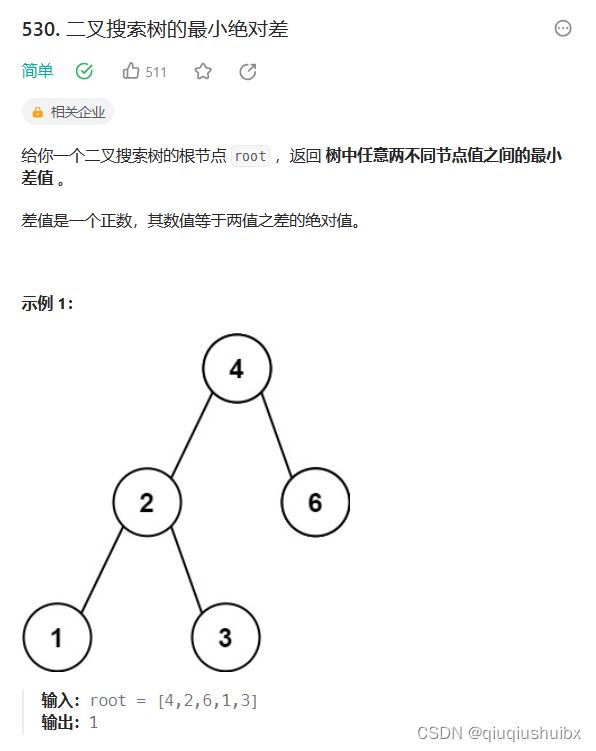
LeetCode T530 二叉搜索树的最小绝对差

题目链接:530. 二叉搜索树的最小绝对差 - 力扣（LeetCode）

 

题目思路:

这题的双指针思路和上一题是一样的,我们用一个result来记录两个数的差,依次比较做更新即可,注意result取int的最大值即可.

题目代码:

class Solution {
    TreeNode pre;
    int result = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        if(root == null)
        {
            return 0;
        }
        getMinimumDifference(root.left);
        if(pre != null)
        {
            int tmp = root.val - pre.val;
             if(tmp

LeetCode T501 二叉搜索树中的众数

题目链接:501. 二叉搜索树中的众数 - 力扣（LeetCode）

 

题目思路:

首先,如果有一个数组你肯定会做,那不就遍历一次找到出现频率最多的数,再遍历一次找到和他出现频率相等的数就行了嘛,这里我们仍然可以使用像前面类似的方式操作,我们说二叉搜索树是有序的,一定要使用前序遍历,这里我们仍然使用递归来解决问题,首先我们需要的是一个指向前面元素的指针,一个count记录当前元素出现的频率,一个maxCount负责更新最大频率

1.递归的参数和返回值

这里我们不需要返回,因为定义好了全局变量直接修改即可,我们的参数就是一个节点

void findMode1(TreeNode root)

2.终止条件

仍然是遇见空节点就直接return

     if(root == null)
        {
            return;
        }

3.定义一次递归的逻辑

首先左右递归的无需多言,重要的是中间的处理时候的环节,我们首先判断count,如果前一个节点等于空或者前一个节点的值不等于后一个节点,count就赋值为1,否则就让count++即可,下面对maxCount进行更新,我们如果发现count大于目前的maxCount,就直接清空我们的List列表,然后加入新的root.val,更新maxCount,如果相等就直接加进去.最后对pre进行移动即可.

        if(pre ==null || pre.val != root.val)
        {
            count = 1;
        }
        else
        {
            count++;
        }
        if(count>maxCount)
        {
            res.clear();
            res.add(root.val);
            maxCount = count;
        }
        else if(count == maxCount)
        {
            res.add(root.val);
        }
        pre = root;

题目代码:

class Solution {
    List res;
    int count;
    int maxCount;
    TreeNode pre;
    public int[] findMode(TreeNode root) {
        res = new ArrayList<>();
        count = 0;
        maxCount = 0;
        pre = null;
        findMode1(root);
        int[] result = new int[res.size()];
        for(int i = 0;imaxCount)
        {
            res.clear();
            res.add(root.val);
            maxCount = count;
        }
        else if(count == maxCount)
        {
            res.add(root.val);
        }
        pre = root;
        findMode1(root.right);
    }
}

LeetCode T236 二叉搜索树的最近公共祖先

题目链接:236. 二叉树的最近公共祖先 - 力扣（LeetCode）

题目思路:

使用后序遍历,最后返回给中节点,如果左右子树都找到就返回root,有其中一方找到就返回其中一方,都没找到就返回null.

1.递归参数返回值

使用原函数

2.终止条件

if (root == null || root == p || root == q) { // 递归结束条件
            return root;
        }

3.单次递归

        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        if(left == null && right == null) { // 若未找到节点 p 或 q
            return null;
        }else if(left == null && right != null) { // 若找到一个节点
            return right;
        }else if(left != null && right == null) { // 若找到一个节点
            return left;
        }else { // 若找到两个节点
            return root;
        }

题目代码:

lass Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) { // 递归结束条件
            return root;
        }

        // 后序遍历
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        if(left == null && right == null) { // 若未找到节点 p 或 q
            return null;
        }else if(left == null && right != null) { // 若找到一个节点
            return right;
        }else if(left != null && right == null) { // 若找到一个节点
            return left;
        }else { // 若找到两个节点
            return root;
        }
        
    }
}

今天的分享就到这里,感谢观看.