LeetCode第四题:寻找两个正序数组的中位数(Java)
题目:寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
示例:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2举例子的图可能比较小,可以双击查看
方法一:合并成一个数组,找中间数。
不考虑最优解的情况下,第一反应就是这个思路。
public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
//合并数组
int[] ints = Arrays.copyOf(nums1, nums1.length + nums2.length);
System.arraycopy(nums2,0,ints,nums1.length,nums2.length);
//排序
Arrays.sort(ints);
int n = ints.length;
int test = n/2;
if ( n % 2 == 0){
return (ints[test]+ints[test-1])/2.0;
}else {
return ints[(n-1)/2];
}
}用Arrays.copyOf()方法得到一个长度为俩数组之和,前面是nums1数组,全新数组。
再用System.arraycopy() 得到一个存储nums1和nums2的数组
对新数组用Arrays.sort排序,找到中位数。奇数直接找中间的数,偶数找中间两个数再除以二。(注意要除以2.0才会回返带小数的部分,除以2的话就直接取整了)
这种思路很简单,无非是合并俩个数组可能方法不同。
Arrays.copyOf(array, size):第一个参数要拷贝的数组对象,第二个参数拷贝的新数组长度。浅拷贝。
System.arraycopy(int[] arr, int star,int[] arr2, int start2, length): 这个方法我不是很常用。
第一个参数被复制的数组,第二个参数被复制数组开始复制的下标,第三个参数目标数组(即要把被复制的数组放到那个数组里),第四个参数目标数组从哪个下标开始放数据,第五个参数被复制的数组中拿几个数值放到目标数组中。
方法二:查找第k个数(左右指针)
我们只要找到中位数所在数组和下标,我们就可以知道中位数是多少了。
我们可以每个数组放一个指针,指向较小数的指针向右移动,直至找到中位数的位置。(即找 数组长度和/2 下标处的数字)
public static double findMedianSortedArrays(int[] A, int[] B) {
int m = A.length;
int n = B.length;
int length = m + n;
//left为A的指针,right为B的指针
int left = 0, right = 0;
//a记录当前位置的值,b记录上一次位置的值
//a记录指针移动前的值
int a = 0, b = 0;
for (int i = 0; i <= length / 2 ; i++) {
b=a;
//边界情况,A已经到最后一位。这时直接B的指针右移
if (left >= m) {
a=B[right];
right++;
continue;
}
//边界情况,B已经到最后一位。这时直接A的指针右移
if (right >= n) {
a=A[left];
left++;
continue;
}
//较小的数指针右移
if (A[left] <= B[right]) {
a=A[left];
left++;
} else {
a=B[right];
right++;
}
}
//长度为偶数
if ((length % 2) == 0) {
return (b+ a) / 2.0;
} else {
//长度为奇数
return a;
}值得注意的点:
考虑边界情况。例如[1,2]和[3,4,5,6] 当i = 2时,left位于A[1]处,这时由于A数组已经没有数字了,在循环就不用考虑A,直接B的指针右移就可以了。若不进行约束A指针继续右移,a=A[left]就会下标越界异常。
为什么要设置a和b记录值?
当长度为偶数,我们不仅要知道当前记录的值还要知道上一次移动时记录的值。两个数/2.0 才能得出中位数。
示例:[1,2] 和 [3,4,5,6] , 每个图是刚进入循环,指针还没有移动时的图。
这种想法思路比较简单,但是写代码时可能会有一些乱。边界可能会被忽略,要注意。算法中很多情况会用到双指针。
方法三:查找第k个数(二分法)
前两种方法的时间和空间消耗都比较大,同时原题有进阶要求时间复杂度为 O(log (m+n)),出现log、有序还是查找一个数最先考虑二分查找了。
我们可以把找中位数转换为找第k小的数。例如[1,2] 和 [3,4,5,6],我们只需要找到这俩个数组第3小和第4小的数时多少,就可以求出中位数了。
与方法二有类似的思路,只不过方法二每次循环只排除一个数字,而方法三每次直接排除一半的数。
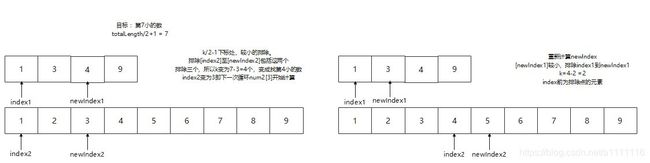
整体思路:我们要找第k小的数(简称k)。二分法,俩个数组各找k/2的数(对应俩数组下标为A[K/2-1] ,B[K/2-1]),较小的一定是k前半部分这部分排除(即第一小到第k/2小的数,不含第k小)。这时候得到一个排除后的新数组,由于我们已经排除第1小到第K/2小的数,我们查找的目标就变成查找第 k-k/2 小的数。直至k=1是,那么查找第一小的数就是我们要查找的中位数。
注意特殊情况:当k/2-1 > length-1 ,即我们要找数组第K/2小,数组没有足够的数去满足,我们只要取数组最后一个元素。当然这时排除也就不会是0到K/2小而是0到length小的数。下一次查找的数就不是k-k/2小而是k-length小数。
public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
int length1 = nums1.length, length2 = nums2.length;
int totalLength = length1 + length2;
int half = totalLength/2;
//长度为奇数,我们要找第length/2+1小的数。
//注意第几小的数和下标不一样的区别,第几小的数-1 等于 下标
if (totalLength % 2 == 1) {
double median = getKthElement(nums1, nums2, half + 1);
return median;
} else {
//长度为偶数,找第length/2小的数 和 第length/2+1小的数
double median = (getKthElement(nums1, nums2, half) + getKthElement(nums1, nums2, half+1)) / 2.0;
return median;
}
}
public static int getKthElement(int[] nums1, int[] nums2, int k) {
//数组下标, nums1简称为A数组 nums2简称为B数组
int index1 = 0, index2 = 0;
while (true) {
//边界情况,A数组已经排除完,不在考虑A数组,找第几小直接从B找就可以了
if (index1 == nums1.length) {
return nums2[index2 + k - 1];
}
//边界情况,B数组已经排除完,不在考虑B数组,找第几小直接从A找就可以了
if (index2 == nums2.length) {
return nums1[index1 + k - 1];
}
//k==1时,俩个数组中较小的就是第k小的数,即目标所求
if (k == 1) {
return Math.min(nums1[index1], nums2[index2]);
}
//min(index1 + k / 2, nums1.length) 防止的特殊情况,[k/2-1]越界。即A数组不够取,没有k/2个数
//[index1] 到 [newIndex1] 为要排除的元素 包括这两个
int newIndex1 = Math.min(index1 + k / 2, nums1.length) - 1;
int newIndex2 = Math.min(index2 + k / 2, nums2.length) - 1;
//较小的就是要排除的数
//排除后新数组第一个元素的下表为index = newIndex + 1;
if (nums1[newIndex1] <= nums2[newIndex2]) {
k = k - (newIndex1 - index1 + 1);
index1 = newIndex1 + 1;
} else {
k = k - (newIndex2 - index2 + 1);
index2 = newIndex2 + 1;
}
}
}举例:[1,3,4,9] 和 [1,2,3,4,5,6,7,8,9]
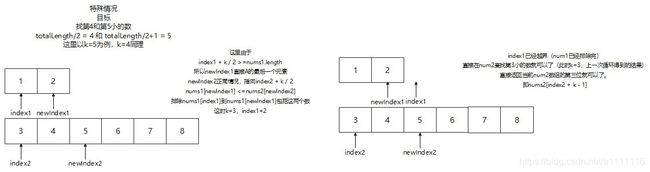
特殊情况:例子[1,2]和[3,4,5,6,7,8]
这种方法无非是通过二分法查找数字,难点是在两个数组中用二分法,明白整体思路还是比较容易理解的。
方法四:官方给的找分割线
一个数组找中位数,我们可以对数组分割。例如[1,2,3,4] 分割后 1 2 || 3 4 ,2和3的平均数就是所需中位数。我们目标就是找到这条分割线。
这个分割线要满足俩个条件 1.左半部分的数都大于右半部分的数 2.左部分数的个数等于右半部分数的个数。若长度为奇数,我们就让左半部分比右半部分多一个数,分割线左边的数就是所求中位数。
扩展到俩个数组时,以[1,2,3,4] [5,6,7,8,9,10,11,12]为例
1 2 3 4||
5 6 || 7 8 9 10 11 12
我们可以知道第一个数组的分割线就可以求得第二个数组的分割线。
设第一个数组长度为 n 分割线前有 i 个元素,第二个数组长度为 m 分割线前有 j 个元素。可知 i + j = n - i + m - j 即俩个数组分割线左部分元素个数和 等于 右部分分割线和,由此可得j = (m+n)/2 -i,这是总长度偶数情况下。
若总的长度为奇数长度,左部分多一个元素。即可得 i + j = n - i + m - j +1(左部分多,要在右部分+1,才能使左右部分元素个数相等),可得j = (m + n +1)/2 -i。
由于i 和 j为整型,+1再除以2 不影响结果,所以总长度奇偶都用j = (m + n +1)/2 -i ,当然你再分奇偶两种情况也可以。
分割线前有i个元素,所以分割线后的元素下标为 i ,分割线前的元素下标为 i-1 。
对第一个数组做二分查找,找到符合条件最大的num[i-1]。
得到分割线后,总长度偶数情况下分割线左部分最大和分割线右部分最小 的平均数就是所求中位数。总长度奇数情况下,左部分最小为中位数。
public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
//始终保持num1长度小于等于 num2长度 num1 简称A数组, num2 简称B数组
if (nums1.length > nums2.length) {
return findMedianSortedArrays(nums2, nums1);
}
int m = nums1.length;
int n = nums2.length;
//A设置左右指针
int left = 0, right = m - 1;
//寻找符合条件最大的A[i-1]
while (left <= right) {
//用二分法查找
//等价于(right+left)/2,但(right-left)/2+left可以防止right和left较大时溢出。
// 以后这种情况下最好用(right-left)/2+left
int i = (right - left) / 2 + left;
int j = (m + n + 1) / 2 - i;
//满足,左指针继续右移,直到找到最大的A[i-1]
if (nums1[i - 1] <= nums2[j]) {
left = i + 1;
} else {
//不满足左边最大 小于等于 右边最小,证明分割线偏右需要向左移。
right = i - 1;
}
}
int i = left, j = (m + n + 1) / 2 - i;
//俩数组分割线左边的数,
//Integer.MIN_VALUE和Integer.MAX_VALUE为边界情况,下面详细说明
int mLeft = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);
int nLeft = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);
//俩数分割线右边的俩个数
int nright = (j == n ? Integer.MAX_VALUE : nums2[j]);
int mright = (i == m ? Integer.MAX_VALUE : nums1[i]);
//分割线左边最大和右边最小
int median1 = Math.max(mLeft, nLeft);
int median2 = Math.min(mright, nright);
//中长度奇偶情况
return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
}这里下标为 i - 1 都为分割线左边的数字 , 下标 i 为分割线右边的数字
解释两个疑问:
1.为什么 if (nums1[i - 1] > nums2[j]) ,怎么确认nums1[i - 1]是左边最大,而不是nums2[j-1]
满足左边最大小于右边最小,要满足四个条件那么他肯定满足。即 nums1[i - 1] <= nums1[ i ] ,nums1[i - 1] <= nums2[ j ] ,nums1[j - 1] <= nums1[ j ] ,nums1[j - 1] <= nums2[ i ] 四个条件
这四个条件意思是,num1分割线左边 小于等于 右边(指num1分割线右边) ,num1分割线左边 小于等于 num2分割线右边,num2分割线左边 小于等于 右边 ,num2分割线左边 小于等于 num1分割线右边。
由于数组有序所以nums1[i - 1] <=nums1[ i ]和nums1[j - 1] <=nums1[ j ] 无论什么情况一定满足。
只需要满足nums1[i - 1] <= nums2[ j ] 和nums1[j - 1] <= nums2[ i ] 即可。这时证明为什么只要 nums1[i - 1] <= nums2[ j ]
j = (m + n + 1) / 2 - i ∈[ 0,n ] ,i ∈ [0, m] 。我们一定可以在[0, m]内得到符合条件的 i,既而得到 j (m一定要大于你,否则 j 可能出现负数)。因为 i 已经是最大符合条件的 i ,那么 i + 1 一定不符合条件 num[ i ] <= num2[ j-1 ],把 i + 1代入 得到 num1[i] <= num2[j-1] 这时不满足。那么他取反就一定满足,即 num1[i] > num2[j-1] 。这时我们可以观察到num1[i] > num2[j-1] 与 所设条件 nums1[i - 1] <=nums1[ i ] 仅差一个等号,而所设条件更加严格限制不满足的条件(else情况下所设条件更加严格)。
2.为什么要有Integer.MIN_VALUE和Integer.MAX_VALUE
这是为了边界情况。
如例子 1 2 3 4|| ,这时要取分割线右边没有数,i就会下标越界异常,我们设为无限大,防止越界。同时也不影响比较分割线右边最小值。
|| 1 2 3 4 ,分割线左边没有数,i - 1就会下标越界异常,我们设为无限小,防止越界。同时也不影响比较分割线左边边最大值。
示例[1,2,3,4] [5,6,7,8,9,10,11,12]
1 || 2 3 4
5 6 7 8 9 || 10 11 12
满足条件,左指针继续右移,直至找到最大的num1[i-1]。进入下一次循环
1 2 || 3 4
5 6 7 8 || 9 10 11 12
满足条件,左指针继续右移,直至找到最大的num1[i-1]。进入下一次循环
1 2 3 || 4
5 6 7 || 8 9 10 11 12
这时left = 4 ,right = 3 退出循环。
i = 4, j = 2这时分割线位置确定
1 2 3 4 ||
5 6 || 7 8 9 10 11 12
数组num1 分割线 左边为4 右边无穷大
数组num2 分割线 左线6 右边为 7
分割线左边最大和右边最小的平均数即为所求。即 (6+7)/ 2.0
这种思路主要是确认分割线位置,实在不懂可以自己debug跑一边画图。
这种算法只能用于这道(找中位数)。方法三,还可以演变为找第k大,找那个数都可以,更具有通用性。
自己学习到或再需要学的东西(总结):
有时间看下Arrays工具类各种操作怎么实现的,用起来很方便,但依旧改变不了时间复杂度。
这题主要学习,两个有序数组怎么找第k小的数。
再复习下各种常用查找和排序算法。
双指针特别常用。
想有点难度的算法都画个图,然而没找到合适的画图软件(现在用的亿图图示,并不怎么好用),画图也比较浪费时间,还是直接像算法四那样演示例子吧。