acwing算法基础课-第五章 动态规划

动态规划

动态规划重要的是思想，虽然没有模板，但有套路，根据实际问题进行相应变化，具体问题具体分析。

背包问题

背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题，即在总重量不超过W的前提下，总价值是否能达到V？它是在1978年由Merkle和Hellman提出的。

背包问题主要分类

图片来自糖豆爸爸

AcWing 2.01 背包问题（0-1 背包问题模板题）

思想

yxc 套路-分析法

强烈推荐该篇博客，关于优化问题讲的很好，
将本例题弄懂了，其它背包问题也便不在话下了
Cloudeeeee

这里记录一下我遇到的问题：
优化操作为什么可以删掉原来的 f[i][j] = f[i - 1][j]; ？
由于第 i 层只与 第 i - 1 层有关，我们可以仅保留上一层结果，将其优化为 一维
在优化后的代码中，在f[j] = max(f[j], f[j - v[i]] + w[i]); 中，
对于红色标记， f[j] = max(f[j], f[j - v[i]] + w[i]);
f[j]相当于 f[ i - 1 ][ j ]，即上一层的f[ j ].

解法代码

二维未优化

//二维未优化 
#include
#include
using namespace std;
const int N = 1010;

int f[N][N];
int v[N];
int w[N];

int main()
{
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	
	
	for(int i = 1; i <= n; i++)
	for(int j = 0; j <= m; j++)
	{
		f[i][j] = f[i - 1][j];
		if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
	}
	cout << f[n][m] << endl;
	return 0;
 } 

一维优化

//一维 
#include
#include
using namespace std;
const int N = 1010;

int f[N];
int v[N];
int w[N];

int main()
{
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	
	for(int i = 1; i <= n; i++)
	for(int j = m; j >= v[i]; j--)
	f[j] = max(f[j], f[j - v[i]] + w[i]);
	
	cout << f[m] << endl;
	return 0;
 }   

AcWing 3. 完全背包问题（ 完全背包问题模板题）

思想

yxc 套路-分析法

最开始的想法分析

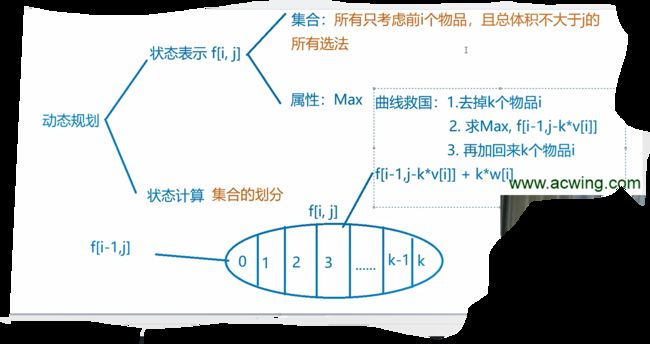
方程改进优化，三层循环变为两层循环

最后，我们可以按照 0-1背包问题的思路再优化成一维

for(int i = 1; i <= n; i++)
	for(int j = v[i]; j <= m; j++)
		f[j] = max(f[j], f[j - v[i]] + w[i]);

注意，这里 j为从 v[ i ] 到m，即顺着推
问：为什么 01背包要倒着推，完全背包要顺着推？

（1）. 对于 01 背包，
操作代码为

二维
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);

一维
f[j] = max(f[j], f[j - v[i]] + w[i]);

对于
f[ j ]，我所需要求的是 f[ i - 1][ j - v[ i ] ]，而逆序可以实现该操作，
不逆序求得是 f[ i ][ j - v[ i ] ]，不符合 01 背包要求

（2）. 对于完全背包问题
操作代码为

//二维进化
f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);

//再进化. 一维
f[j] = max(f[j], f[j - v[i]] + w[i]);

对于
f[ j ]，我所需要求的是 f[ i ][ j - v[ i ] ]，不需要逆序

总结，对于要不要逆序，如果状态转移时用的是上一层的状态则需要逆序枚举求体积；
如果状态转移时用的是本层的状态则不需要逆序枚举求体积
（完全背包在二维原始代码中，用的是上一层的状态，但经过方程转换，变成了用本层的状态）

解法代码

二维原始代码，易超时

//二维 
#include
#include
using namespace std;
const int N = 1010;
int f[N][N];
int v[N], w[N];

int main()
{
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	
	for(int i = 1; i <= n; i++)
	for(int j = 0; j <= m; j++)
	for(int k = 0; k * v[i] <= j; k++)
	f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
	
	cout << f[n][m] << endl;
	return 0;
}

二维进化. 方程转换，将第三层 k 消去

// 进化. 方程转换，将第三层 k 消去  
#include
#include
using namespace std;
const int N = 1010;
int f[N][N];
int v[N], w[N];

int main()
{
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	
	for(int i = 1; i <= n; i++)
	for(int j = 0; j <= m; j++)
	{
		f[i][j] = f[i - 1][j];
		if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
	}
	cout << f[n][m] << endl;
	return 0;
}

再进化. 一维

// 再进化. 一维
#include
#include

using namespace std;
const int N = 1010;
int f[N];
int v[N], w[N];

int main()
{
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	
	for(int i = 1; i <= n; i++)
	for(int j = v[i]; j <= m; j++)
		f[j] = max(f[j], f[j - v[i]] + w[i]);
	
	cout << f[m] << endl;
	return 0;
}

AcWing 4. 多重背包问题 I （ 多重背包朴素法模板题）

思想

yxc 套路-分析法

该题与上一题类似，只是要求第 i 件物品最多选 s[i] 个，加上该条件即可，

解法代码

#include
#include
using namespace std;
const int N = 110;

int f[N][N];
int v[N], w[N], s[N];

int main()
{
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
	
	for(int i = 1; i <= n; i++)
	for(int j = 0; j <= m; j++)
	for(int k = 0; j >= k * v[i] && k <= s[i]; k++)
	f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
	
	cout << f[n][m] << endl;
	return 0;
 } 

AcWing 5. 多重背包问题 II ( 多重背包二进制优化模板题)

思想

多重背包问题 I 的求法容易超时，所以我们可以用二进制优化 s( s表示每种物品的数量)

图片来自
Cloudeeeee

至于
1 ~ n 的某个数可以由其优化的二进制组数物品凑出，且每组物品不超过一次
的数学原理证明也是很简单的，大家模拟一下 1~ 200 的的数据便会懂了。

解法代码

#include
#include
using namespace std;
const int N = 12000;
const int M = 2010;

int v[N];
int w[N];
int f[M];

int main()
{
	int n, m;
	cin >> n >> m;
	int cnt = 0;
	for(int i = 1; i <= n; i++)
	{
		int a, b, s;
		scanf("%d%d%d", &a, &b, &s);
		int k = 1;
		while(k <= s)
		{
			cnt++;
			v[cnt] = a * k;
			 w[cnt] = b * k;
			 s -= k;
			 k *= 2;
		}
		if(s > 0)
		{
			cnt++;
			v[cnt] = a * s;
			w[cnt] = b * s;
		}
	}
	n = cnt;
	
	for(int i = 1; i <= n; i++)
	for(int j = m; j >= v[i]; j--) 
	f[j] = max(f[j], f[j - v[i]] + w[i]);
	
	cout << f[m] << endl;
	return 0;
 } 

AcWing 9. 分组背包问题（分组背包模板题）

思想

解法代码

#include
#include 
using namespace std;
const int N = 110;

int v[N][N];
int w[N][N];
int f[N];
int s[N]; //用于表示第 i个物品组的物品数量 

int main()
{
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++)
	{
		cin >> s[i];
		for(int j = 0; j < s[i]; j++)
		cin >> v[i][j] >> w[i][j];//表示第 i组第 j个物品的体积和价值
	}
	
	for(int i = 0; i <= n; i++)
	for(int j = m; j >= 0; j--)
	for(int k = 0; k < s[i]; k++)
		if(v[i][k] <= j)
		f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
		
	cout << f[m] << endl;	 
	return 0; 
}

线性DP

AcWing 898. 数字三角形

题目解析：Cloudeeeee

#include
#include
using namespace std;
const int N = 510;

int f[N][N];
int a[N][N];

int main()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i++)
	for(int j = 1; j <= i; j++)
		scanf("%d", &a[i][j]);
	//注意初始化，考虑该节点的左上与右上 
	for(int i = 0; i <= n; i++)
// j = i + 1时,即考虑最右端加一位的初始化,因为要考虑下一层最右端的右上方 
	for(int j = 0; j <= i + 1; j++) 
		f[i][j] = - 1e8;
		
    // 初始化f[1][1],因为是从这里开始的 
	f[1][1] = a[1][1];
	
	for(int i = 2; i <= n; i++)
	for(int j = 1; j <= i; j++)
	f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
	
	// max值可能在最后一层的任一位置 
	int res = -1e9;
	for(int i = 1; i <= n; i++)
	 res = max(res, f[n][i]);
	 
	 cout << res << endl;
	
	return 0;
} 

AcWing 895 最长上升子序列

题目解析：可以参考这位博主博客 Cloudeeeee

#include
#include
using namespace std;
const int N = 1010;

int f[N]; // f[i], 所有以 i 结尾的上升子序列中 序列长度最大的值  
int a[N];

int main()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	
	for(int i = 1; i <= n; i++)
	{
		f[i] = 1; //最小为 1 
		for(int j = 1; j < i; j++)
			if(a[i] > a[j])
			f[i] = max(f[i], f[j] + 1);
	}
	
	int res = -1e9;
	for(int i = 1; i <= n; i++)
	res = max(res, f[i]);
	
	cout << res << endl;
	return 0;
}

找出并打印最长上升子序列

#include
#include
using namespace std;
const int N = 1010;

int f[N];  // f[i], 所有以 i 结尾的上升子序列中 序列长度最大的值 
int a[N];
int g[N]; //用于标记 f[i]的上一个字符下标 

int main()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	
	for(int i = 1; i <= n; i++)
	{
		f[i] = 1;
		for(int j = 1; j < i; j++)
			if(a[i] > a[j])
//这里下面加了一条判断语句，f[i]不再是 max(f[i], f[j] + 1);
//因为f[i]依旧为 max(,)的话，
//只要 f[j] < f[i], g[i]便会 = j;即 g[i]标记的是左边离 f[i]最近的比 f[i]小的下标 
//而我们需要的是其 1 ~ i-1 中 f[]值最大的下标，即下面的变换		 
				if(f[i] < f[j] + 1)
			{
				f[i] = f[j] + 1;
				g[i] = j; 
			}
	}
	
	
	int res = -1e9;
	int k = 1;
	for(int i = 1; i <= n; i++)
		if(f[k] < f[i])
			k = i;
	
	int len = f[k];
	for(int i = 1; i <= len; i++)
	{
		cout << a[k] << " ";
		k = g[k];
	}
	return 0;
}

AcWing 896 最长上升子序列 II

题目解析：可以参考这位博主博客 Cloudeeeee

核心点：对于每个长度的最大上升子序列，其末尾值最小（有利于构成下一个长度加一的大上升子序列）
长度为 i 的最大上升子序列末位置值肯定比长度为 i - 1的最大上升子序列末位置值大 ，如果不是的话，即如果 i 的最大上升子序列末位置值小于等于 i - 1的最大上升子序列末位置值，那么对于长度为 i 的最大上升子序列，倒数第二个位置（i - 1）值必定小于长度为 i - 1的最大上升子序列末位置值，这就不符合最上升子序列的性质了

 
#include
#include
using namespace std;
const int N = 100010;

int a[N];
int q[N];

int main()
{
	int n;
	cin >> n;
	int len = 0;
	for(int i = 0; i < n; i++) cin >> a[i];
	
	for(int i = 0; i < n; i++)
	{
		int l = 0;
		int r = len;
		while(l < r)
		{
			int mid = (l + r + 1) / 2;
			if(q[mid] < a[i]) l = mid;
			else r = mid - 1;
		}
		len = max(len, r + 1);
		q[r + 1] = a[i];
	}
	
	cout << len << endl;
	
	return 0;
 } 

AcWing 897 最长公共子序列

题目解析：来自 Cloudeeeee

#include
#include
using namespace std;
const int N = 1010;

int f[N][N];
char a[N], b[N];

int main()
{
	int n, m;
	cin >> n >> m;
	scanf("%s%s", a + 1, b + 1);
	for(int i = 1; i <= n; i++)
	for(int j = 1; j <= m; j++)
	{
		f[i][j] = max(f[i - 1][j], f[i][j - 1]);
		if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
	}
	cout << f[n][m] << endl;	
	return 0;
  }  

AcWing 902 最短编辑距离

图片来自：Cloudeeeee

初始化问题

图片来自糖豆爸爸

#include 
#include
using namespace std;
const int N = 1010;

int f[N][N];
char a[N], b[N];

int main()
{
	int n, m;
	scanf("%d%s", &n, a + 1);
    scanf("%d%s", &m, b + 1);
	
	//初始化 	
	for(int i = 0; i <= m; i++) f[0][i] = i;// a初始长度为 0，a只能作添加操作
	for(int i = 0; i <= n; i++) f[i][0] = i;// b初始长度为 0，a只能作删除操作
	
	for(int i = 1; i <= n; i++)
	for(int j = 1; j <= m; j++)
	{   //删除和插入 
		f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
		//相等 
		if(a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
		//替换 
		else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
	}
	
	cout << f[n][m] << endl;
	return 0;
}

AcWing 899 编辑距离

题目解析：在上题的基础上，对于给定的 n 个字符串，每次判断最小编辑距离是否小于上限操作次数即可

#include 
#include
#include
using namespace std;
const int N = 15;
const int M = 1010;

int f[N][N];
char str[M][M];

int  edit_distance(char a[], char b[])
{
	int la = strlen(a + 1), lb = strlen(b + 1);
	
	for(int i = 0; i <= la; i++) f[0][i] = i;
	for(int i = 0; i <= lb; i++) f[i][0] = i;
	
	for(int i = 1; i <= la; i++)
	for(int j = 1; j <= lb; j++)
	{   //删除和插入 
		f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
		//相等 
		if(a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
		//替换 
		else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
	}
	return f[la][lb];
}
 
int main()
{
	int n, m;
	cin >> n >> m;
	for(int i = 0; i < n; i++) scanf("%s", str[i] + 1);	
	while(m--)
	{
		char s[N];
		scanf("%s", s + 1);
		int limit;
		scanf("%d", &limit);
		int res = 0;
		for(int i = 0; i < n; i++)
		if(edit_distance(str[i], s) <= limit) res++;
		
		printf("%d\n", res);
	}	
	return 0;
}

区间DP

AccWing 282 石子合并

题目解析：

划分的方法是从 i 到 j 中遍历从i ， i + 1 , … ， j- 1， j划分时的代价，取最小值

转载来自Cloudeeeee

思路分析：参考 蒟蒻豆进阶之路

#include
#include
#include
using namespace std;
const int N = 310;

int f[N][N];
int a[N];

int main()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];

	for(int i = 1; i <= n; i++) 
	a[i] = a[i] + a[i - 1];
	
	for(int len = 2; len <= n; len++)
	for(int i = 1; i + len - 1 <= n; i++)
	{
		int l = i, r = i + len - 1;
		//注意，长度为 1的堆，即自己和自己是不需要合并的，已经初始化为0
		f[l][r] = 1e9 ;  
		for(int k = l; k < r; k++)
		f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + a[r] - a[l - 1]);
	}
	
	cout << f[1][n] << endl;
	return 0;
 } 

计数类DP

AcWing 900 整数划分

解析本题：参考该篇博客 Cloudeeeee

//转换成完全背包问题 
#include
#include
using namespace std;

const int N = 1010;
const int eps = 1e9 + 7; 
int f[N];

int main()
{
	int n;
	cin >> n;
	f[0] = 1; //容积为 0，1 ~ i中物品都不选也是种方案 
	for(int i = 1; i <= n; i++)
	for(int j = i; j <= n; j++)
	f[j] = (f[j] + f[j - i]) % eps;
	
	cout << f[n] << endl;
	return 0; 
}

数位统计DP

AcWing 338 计数问题

题目解析：Cloudeeeee

#include
#include
#include
using namespace std;

// 由 l ~ r 'a' 'b' 'c' 组成 “abc”  
int get(vector<int> num, int l, int r)
{
	int res = 0;
	for(int i = l; i >= r; i--) res = res * 10 + num[i];
	return res;
}
//求 10 的 i 次方 
int power10(int i)
{
	int res = 1;
	while(i--) res *= 10;
	return res;
}

//求 1 ~ n 中，x 出现的次数 
int count(int n,int x)
{
	if(!n) return 0;
	vector<int> num;
	int res = 0;
	//倒着存 
	while(n)
	{
		num.push_back(n % 10);
		n /= 10;
	}
	
	n = num.size();
	for(int i = n - 1 - !x; i >= 0; i--) //对于 0，从第二位开始 
	{
		if(i < n - 1)
		{
			res += get(num, n - 1, i + 1) * power10(i);
			if(!x) res -= power10(i); // x 等于 0时，减去不合法的首位计数 
		}
		if(num[i] == x) res += get(num, i - 1, 0) + 1;
		else if(num[i] > x) res += power10(i);
	}
	return res;
}

int main()
{
	int a, b;
	while(scanf("%d%d", &a, &b) && (a || b))
	{
		
		if(a < b) swap(a, b);
		for(int i = 0; i <= 9; i++)
		{
			//类似前缀和，a - (b - 1) 
			int t = count(a, i) - count(b - 1, i);
			printf("%d ", t);
		}
		puts("");
	}
	return 0;
 } 

状态压缩DP

AcWing 291 蒙德里安的梦想

题目解析：阿正的梦工坊

关于f[0][0] = 1,答案为f[m][0] 可以看acwing题解大家的讨论
题目链接：AcWing 291 蒙德里安的梦想

#include
#include
#include
#include
using namespace std;

const int N = 12;
const int M = 1 << N;
typedef long long LL;

LL f[N][M];            //第一维表示列， 第二维表示所有可能的状态
vector<int> state[M]; //记录合法的状态 
bool st[M];          // 判断是否有奇数个连续的0 

int main()
{
	int n , m;
	while((cin >> n >> m) && (n || m))
	{
		//第一部分
		// 预处理每列不能有奇数个连续的0
		for(int i = 0; i < 1 << n; i++)
		{
			int cnt = 0;
			bool isvalid = true;
			for(int j = 0; j < n; j++)
			{
				if(i >> j & 1)
				{
					if(cnt & 1) 
					{
						isvalid = false;
						break;
					}
					cnt = 0;
				}
				else cnt++;
			}
			if(cnt & 1) isvalid = false;
//虽然输入包含多组测试用例。,
//但st[]不用初始化，因为每次要用的范围都会进行赋值 
			st[i] = isvalid;
		}
		//第二部分；
		//看第i-2列伸出来的和第i-1列伸出去的是否冲突 
		for(int i = 0; i < 1 << n; i++)
		{
			state[i].clear(); //输入包含多组测试用例，每次需要初始化 
			for(int j = 0; j < 1 << n; j++)
			if((i & j) == 0 && st[i | j] )
		 	state[i].push_back(j); 
		 } 
		 
		 //第三部分，dp 
		 memset(f, 0, sizeof f);
		 f[0][0] = 1;
		 for(int i = 1; i <= m; i++)
		 for(int j = 0; j < 1 << n; j++)
		 for(auto k : state[j])
		 f[i][j] += f[i - 1][k];
		
		cout << f[m][0] << endl; 
	}
	return 0;
 } 

AcWing 最短Hamilton路径

题目解析：

图片来自 Cloudeeeee

#include
#include
#include
using namespace std;
const int N = 20;
const int M = 1 << N;
int f[M][N];
int w[N][N];

int main()
{
	int n;
	cin >> n;
	for(int i = 0; i < n; i++)
	for(int j = 0; j < n; j++)
	cin >> w[i][j];
	
	memset(f, 0x3f, sizeof f);
	//表示只包含节点 0 的状态，即起点和终点相同的情况下的路径长度为 0。
	f[1][0] = 0; 
	
	for(int i = 0; i < 1 << n; i++)
	for(int j = 0; j < n; j++)
	if(i >> j & 1)
	{
		for(int k = 0; k < n; k++)
		if((i - (1 << j)) >> k & 1)
		f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
	}
	
	cout << f[(1 << n) - 1][n - 1] << endl;
	return 0;
 } 

树形DP

AcWing 285 没有上司的舞会

题目解析；
Cloudeeeee

#include
#include
#include
using namespace std;
const int N = 6010;

int e[N], h[N], ne[N], idx;
int f[N][2];
bool has_fa[N];
int happy[N];

void add(int a, int b)
{
	e[idx] = b; ne[idx] = h[a], h[a] = idx++;
}

void dfs(int root)
{
	f[root][1] = happy[root];
	for(int i = h[root]; i != -1; i = ne[i])
	{
		int j = e[i];
		dfs(j);
		f[root][0] += max(f[j][0], f[j][1]);
		f[root][1] += f[j][0];
	}
}

int main()
{
	int n;
	cin >> n;
	memset(h, -1, sizeof h);
	//从 1开始，因为后面邻接表 h[i], i >= 1，h[0]不存数据 
	//同时，在 h[root]时，root 不能为 0，同样道理。  
	for(int i = 1; i <= n; i++) cin >> happy[i];
	
	for(int i = 0; i < n - 1; i++)
	{
		int l, k;
		cin >> l >> k;
		add(k, l);
		has_fa[l] = true; 
	}
	int root = 1;
	while(has_fa[root]) root++;
	
	dfs(root);
	
	cout << max(f[root][1], f[root][0]) << endl;
	return 0;
 } 

记忆化搜索

AcWing 901 滑雪

题目解析：糖豆爸爸

#include
#include
#include
using namespace std;
const int N = 310;
int r, c;

int f[N][N];
int h[N][N];

int lx[4] = {-1, 0, 1, 0};
int ly[4] = {0, 1, 0, -1};

int dp(int x, int y)
{
	if(f[x][y] != -1) return f[x][y];
	f[x][y] = 1;
	for(int i = 0; i < 4; i++)
	{
		int ex = x + lx[i], ey = y + ly[i];
		if(ex >= 0 && ey >= 0 && ex < c && ey < r)
			if(h[x][y] > h[ex][ey])
			f[x][y] = max(f[x][y], dp(ex, ey) + 1);
	}
	return f[x][y];
}
int main()
{
	cin >> r >> c;
	for(int i = 0; i < r; i++)
	for(int j = 0; j < c; j++)
	cin >> h[i][j];
	
	memset(f, -1, sizeof f);
	
	int res = -1;
	for(int i = 0; i < r; i++)
	for(int j = 0; j < c; j++)
	res = max(res, dp(i , j));
	
	cout << res << endl;
	
	return 0;
 }