【王道考研 数据结构 】基础算法代码复习总结 C语言(树和图）

一、树和二叉树

树的遍历

#include 
#include 

typedef struct BiTNode {
	ElemType data;
	struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

//先序遍历
//递归
void PreOrder(BiTree T) {
	if (T != NULL) {
		visit(T);
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}

//非递归
void PreOrder2(BiTree T) {
	InitStack(S);
	BiTree p = T;
	while (p || !IsEmpty(S)) {
		if (p) {
			visit(p);
			Push(S, p);
			p = p->lchild;
		} else {
			Pop(S, p);
			p = p->rchild;
		}
	}
}

//中序遍历
//递归
void InOrder(BiTree T) {
	if (T != NULL) {
		InOrder(T->lchild);
		visite(T);
		InOrder(T->rchild);
	}
}

//非递归
void InOrder2(BiTree T) {
	InitStack(S);
	BiTree p = T;
	while (p || !IsImpty(S)) {
		if (p) {
			push(S, p);
			p = p->lchild;
		} else {
			Pop(S, p);
			visit(p);
			p = p->rchild;
		}
	}
}

//后序遍历

void PostOrder(BiTree T) {
	if (T != NULL) {
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		visit(T);
	}
}

//层次遍历
void LevelOrder(BiTree T) {
	InitQueue(Q);
	BiTree p;
	EnQueue(Q, T);
	while (!Empty(Q)) {
		DeQueue(Q, p);
		visit(p);
		if (p->lchild != NULL)
			EnQueue(Q, p->lchild);
		if (p->rchild != NULL)
			EnQueue(Q, p->rchild);
	}
}

线索二叉树

#include 

typedef struct ThreadNode {
	ElemType data;
	struct ThreadNode *lchild, *rchild;
	int ltag, rtag;
} ThreadNode, *ThreadTree;

//中序线索二叉树
//递归
void InThread(ThreadTree &p, ThreadTree &pre) {
	if (p != NULL) {
		InThread(p->lchild, pre);	//递归，线索化左子树
		if (p->lchild == NULL) {	//左子树为空，建立前驱线索
			p->lchild = pre;
			p->ltag = 1;
		}
		if (pre != NULL && pre->rchild == NULL) {
			pre->rchild = p; //建立前驱节点的后继线索
			pre->rtag = 1;
		}
		pre = p;	//标记当前结点为刚刚访问过的结点
		InThread(p->rchild, pre);
	}
}

void CreatInThread(ThreadTree T) {
	ThreadTree pre = NULL;
	if (T != NULL) {
		InThead(T, pre);
		pre->rchild = NULL; //处理遍历的最后一个结点
		pre->rtag = 1;
	}
}

遍历

//中序线索树的遍历
ThreadNode *Firstnode(ThreadNode *p){
	while(p->ltag==0)
		p=p->lchild;
		return p;
}
ThreadNode *Nextnode(ThreadNode *p){
	if(p->rtag==0)
	return Firstnode(p->rchild);
	else
		return p->rchild;
}
//不含头结点的中序线索树的中序遍历
void Inorder(ThreadNode *T){
	for(ThreadNode *p=Firstnode(T);p!=NULL;p=Nextnode(p))
		visit(p);
}

二、图

BFS

广度优先搜索
主要使用队列实现，对每个节点可能到达的路径进行入队出队判断

#include 
#define MaxVertexNum 100
typedef char VertexType;
typedef int EdgeType;
int Max = 0x3f3f3f3f;

typedef struct {
	VertexType Vex[MaxVertexNum];
	EdgeType EdgeType[MaxVertexNum][MaxVertexNum];
	int vexnum, arcnum;
} Gragh;

//BFS遍历
bool visited[MaxVertexNum];
void BFSTraverse(Graph G) {
	for (int i = 0; i < G.vexnum; ++i)
		visited[i] = false;
	InitQueue(Q);
	for (int i = 0; i < G.vexnum; ++i)
		if (!visited[i])
			BFS(G, i);

}

void BFS(Graph G, int v) {
	visit(v);
	visited[v] = true;
	Enqueue(Q, v);
	while (!isEmpty(Q)) {
		DeQueue(Q, v);
		for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))
			if (!visited[w]) {
				visit(w);
				visited[w] = true;
				EnQueue(Q, w);
			}
	}
}

//BFS求单源最短路径
void BFS_MIN_Distance(Graph G, int u) {
	for (int i = 0; i < G.vexnum; i++)
		d[i] = Max; //初始化路径为无穷
	visited[u] = true;
	d[u] = 0;
	EnQueue(Q, u);
	while (!isEmpty(Q)) {
		DeQueue(Q, u);
		for (w = FirstNeighbor(G, u); w >= 0; w = NextNeighbor(G, u, w))
			if (!visited[w]) {
				visited[w] = true;
				d[w] = d[u] + 1;
				EnQueue(Q, w);
			}

	}
}

DFS

深度优先搜索

bool visited[MAX_VERTEX_NUM];
void DFSTraverse(Graph G){
	for(v=0;v<G.vexnum;++v)
		visited[v]=FALSE;
	for(v=0;v<G.vexnum;++v)
		if(!visited[v])
			DFS(G,v);
}
void DFS(Graph G,int v){
	visit(v);
	visited[v]=TRUE;
	for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
		if(!visited[w]){
			DFS(G,w);
	}
}

最小生成树

关于图的几个概念定义：

连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。
强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。
连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

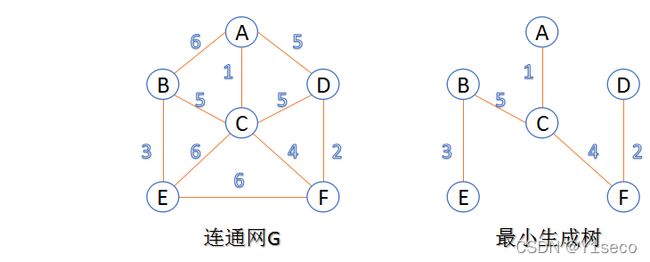
下面介绍两种求最小生成树算法

1.Kruskal算法
此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

把图中的所有边按代价从小到大排序；
把图中的n个顶点看成独立的n棵树组成的森林；
按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

2. Prim算法
   此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;
在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。
重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。
由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息，：

struct
{
  char vertexData   //表示u中顶点信息
  UINT lowestcost   //最小代价
}closedge[vexCounts]

Prim算法

最小生成树是一个图的极小连通子图，它包含原图的所有顶点，并且所有边的权值之和尽可能小。

Prim算法就是图的最小生成树算法之一，Prim 算法是一种求解加权无向连通图的 MST 问题的贪心算法。它能找出一个边的子集，使得其构成的树包含图中所有顶点，且边的权值之和最小。

Prim算法以图的顶点为基础，从首个初始顶点，寻找到达其他顶点权值最小的边，并把该顶点加入到“已到达顶点”的集合中，此时，这个集合就是这个图的最小生成树。

一般用一维数组比较方便表达最小生成树，数组下标所对应的元素，代表该顶点在最小生成树当中的父亲节点。

// 基于Prim算法实现最小生成树
#include 
#include 
const int INF = 1e7;

using namespace std;

vector<vector<int>> Init() {
    int n, m;
    cout << "请输入带权无向图的定点数和边数(以空格隔开):" << endl;
    cin >> n >> m;
    vector<vector<int>> graph(n+1, vector<int>(n+1, INF));
    cout << "请依次输入" << m << "条边的开始节点，结束节点，权值(以空格隔开):" << endl;
    int start, end, wet;
    for (int i = 0; i < m; i++) {
        cin >> start >> end >> wet;
        graph[start][end] = wet;
        graph[end][start] = wet;
    }

    return graph;
}

int Prim(vector<vector<int>>& c, int u) {
    int n = c.size() - 1;
    // 定义数据结构lowcost[]，closest[]，s[]
    vector<int> lowcost(n+1);
    vector<int> closest(n+1);
    vector<bool> s(n+1);

    /// 1.初始化lowcost[]，closest[]，s[]
    s[u] = true;
    for (int i = 1; i <= n; i++) {
        if (i != u) {
            lowcost[i] = c[u][i];
            closest[i] = u;
            s[i] = false;
        }
        else
            lowcost[i] = 0;
    }


    // n个节点之间需要找最短路径n-1次
    for (int i = 0; i < n-1; i++) { 
        // 2.找最小
        int tmp = INF, t = u;
        for (int j = 1; j <= n; j++) {
            if (!s[j] && (lowcost[j] < tmp)) {   //!s[j]表示j节点V-U集合中
                t = j;
                tmp = lowcost[j];
            }
        }
        // 找不到，跳出循环
        if (t == u) break;

        // 将t加入集合U
        s[t] = true;  

        // 3.更新
        for (int j = 1; j <= n; j++) {
            if ((!s[j]) && (c[t][j] < lowcost[j])) {
                lowcost[j] = c[t][j];
                closest[j] = t;
            }
        }
    }

    // 4.打印最终结果
    int totalcost = 0;
    cout << "lowcost[]数组：";
    for (int i = 1; i <= n; i++) {
        cout << lowcost[i] << " ";
        totalcost += lowcost[i];
    }
    cout << endl;
    cout << "closest[]数组：";
    for (int i = 1; i <= n; i++) {
        cout << closest[i] << " ";
    }
    cout << endl;
    return totalcost;
}

// test main()
int main() {
    vector<vector<int>> graph = Init();
    int weight = Prim(graph, 1); // 1表示从1开始找
    cout << "\n最小生成树总的花费是：" << weight << endl;
}

实验结果
请输入带权无向图的定点数和边数(以空格隔开):
7 12
请依次输入12条边的开始节点，结束节点，权值(以空格隔开):
1 2 23
1 6 28
1 7 36
2 3 20
2 7 1
3 4 15
3 7 4
4 5 3
4 7 9
5 6 17
5 7 16
6 7 25
lowcost[]数组：0 23 4 9 3 17 1
closest[]数组：0 1 7 7 4 5 2

最小生成树总的花费是：57

D:\projects\test\x64\Release\test.exe (进程 1788)已退出，返回代码为: 0。

Kruskal算法

/************************************************************************
CSDN 勿在浮沙筑高台 http://blog.csdn.net/luoshixian099算法导论--最小生成树（Prim、Kruskal）2016年7月14日
************************************************************************/
#include 
#include 
#include 
#include 
using namespace std;
#define INFINITE 0xFFFFFFFF   
#define VertexData unsigned int  //顶点数据
#define UINT  unsigned int
#define vexCounts 6  //顶点数量
char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
struct node 
{
    VertexData data;
    unsigned int lowestcost;
}closedge[vexCounts]; //Prim算法中的辅助信息
typedef struct 
{
    VertexData u;
    VertexData v;
    unsigned int cost;  //边的代价
}Arc;  //原始图的边信息
void AdjMatrix(unsigned int adjMat[][vexCounts])  //邻接矩阵表示法
{
    for (int i = 0; i < vexCounts; i++)   //初始化邻接矩阵
        for (int j = 0; j < vexCounts; j++)
        {
            adjMat[i][j] = INFINITE;
        }
    adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
    adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3;
    adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4;
    adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2;
    adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6;
    adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6;
}
int Minmum(struct node * closedge)  //返回最小代价边
{
    unsigned int min = INFINITE;
    int index = -1;
    for (int i = 0; i < vexCounts;i++)
    {
        if (closedge[i].lowestcost < min && closedge[i].lowestcost !=0)
        {
            min = closedge[i].lowestcost;
            index = i;
        }
    }
    return index;
}
void MiniSpanTree_Prim(unsigned int adjMat[][vexCounts], VertexData s)
{
    for (int i = 0; i < vexCounts;i++)
    {
        closedge[i].lowestcost = INFINITE;
    }      
    closedge[s].data = s;      //从顶点s开始
    closedge[s].lowestcost = 0;
    for (int i = 0; i < vexCounts;i++)  //初始化辅助数组
    {
        if (i != s)
        {
            closedge[i].data = s;
            closedge[i].lowestcost = adjMat[s][i];
        }
    }
    for (int e = 1; e <= vexCounts -1; e++)  //n-1条边时退出
    {
        int k = Minmum(closedge);  //选择最小代价边
        cout << vextex[closedge[k].data] << "--" << vextex[k] << endl;//加入到最小生成树
        closedge[k].lowestcost = 0; //代价置为0
        for (int i = 0; i < vexCounts;i++)  //更新v中顶点最小代价边信息
        {
            if ( adjMat[k][i] < closedge[i].lowestcost)
            {
                closedge[i].data = k;
                closedge[i].lowestcost = adjMat[k][i];
            }
        }
    }
}
void ReadArc(unsigned int  adjMat[][vexCounts],vector<Arc> &vertexArc) //保存图的边代价信息
{
    Arc * temp = NULL;
    for (unsigned int i = 0; i < vexCounts;i++)
    {
        for (unsigned int j = 0; j < i; j++)
        {
            if (adjMat[i][j]!=INFINITE)
            {
                temp = new Arc;
                temp->u = i;
                temp->v = j;
                temp->cost = adjMat[i][j];
                vertexArc.push_back(*temp);
            }
        }
    }
}
bool compare(Arc  A, Arc  B)
{
    return A.cost < B.cost ? true : false;
}
bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree)
{
    unsigned int index_u = INFINITE;
    unsigned int index_v = INFINITE;
    for (unsigned int i = 0; i < Tree.size();i++)  //检查u,v分别属于哪颗树
    {
        if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end())
            index_u = i;
        if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end())
            index_v = i;
    }
 
    if (index_u != index_v)   //u,v不在一颗树上，合并两颗树
    {
        for (unsigned int i = 0; i < Tree[index_v].size();i++)
        {
            Tree[index_u].push_back(Tree[index_v][i]);
        }
        Tree[index_v].clear();
        return true;
    }
    return false;
}
void MiniSpanTree_Kruskal(unsigned int adjMat[][vexCounts])
{
    vector<Arc> vertexArc;
    ReadArc(adjMat, vertexArc);//读取边信息
    sort(vertexArc.begin(), vertexArc.end(), compare);//边按从小到大排序
    vector<vector<VertexData> > Tree(vexCounts); //6棵独立树
    for (unsigned int i = 0; i < vexCounts; i++)
    {
        Tree[i].push_back(i);  //初始化6棵独立树的信息
    }
    for (unsigned int i = 0; i < vertexArc.size(); i++)//依次从小到大取最小代价边
    {
        VertexData u = vertexArc[i].u;  
        VertexData v = vertexArc[i].v;
        if (FindTree(u, v, Tree))//检查此边的两个顶点是否在一颗树内
        {
            cout << vextex[u] << "---" << vextex[v] << endl;//把此边加入到最小生成树中
        }   
    }
}
 
int main()
{
    unsigned int  adjMat[vexCounts][vexCounts] = { 0 };
    AdjMatrix(adjMat);   //邻接矩阵
    cout << "Prim :" << endl;
    MiniSpanTree_Prim(adjMat,0); //Prim算法，从顶点0开始.
    cout << "-------------" << endl << "Kruskal:" << endl;
    MiniSpanTree_Kruskal(adjMat);//Kruskal算法
    return 0;
}

Dijkstra算法(求单源最短路径问题)

算法原理

• 适合求解有回路的带权图的最短路径
• 可以求任意两个顶点的最短路径
• 不适合求带负权值的最短路径问题

具体解释

邻接矩阵实现

#include
#include
#include
#include
using namespace std;

//用邻接矩阵构建有向图
#define MAX 999//表示无穷
#define MVNum 20//最大结点数
typedef int VertexType;//设置结点的数据类型为int型（方便后续修改成char...）
typedef int ArcType;//设置的权值为int型（方便后续修改成float...）

class Graph//Adjacency Matrix Graph有向图，用邻接矩阵表示
{
public:
	void Create();
	int LocateVex(VertexType u);//查找Graph中的顶点u，并返回其对应在顶点表中的下标，未找到则返回-1
	int firstadj(int v);
	int nextadj(int v, int w);
	void Dijkstra(VertexType start_point);//使用迪杰斯特拉算法打印单源最短路径
	void Show();//调试用，打印邻接矩阵
private:
	VertexType vexs[MVNum];//顶点表,将顶点保存的信息存入此处
	ArcType arcs[MVNum][MVNum];//邻接矩阵
	int vexnum, arcnum;//图当前的顶点数和边数
	vector<queue<VertexType>>path;//保存各结点最短路径的path[i]
	ArcType dist[MVNum];//最短路径大小
	bool solved[MVNum];//是否找到最短路径
};
int Graph::LocateVex(VertexType u)
{//查找Graph中的顶点u，并返回其对应在顶点表中的下标，未找到则返回-1
	int i;
	for (i = 0; i < this->vexnum; i++)
	{
		if (u == this->vexs[i])
			return i;
	}
	return -1;
}
int Graph::firstadj(int v)
{
	for (int i = 0; i < this->vexnum; i++)
	{
		if (this->arcs[v][i] != MAX)
			return i;
	}
	return -1;
}
int Graph::nextadj(int v, int w)
{
	for (int i = w + 1; i < this->vexnum; i++)
	{
		if (this->arcs[v][i] != MAX)
			return i;
	}
	return -1;
}
void Graph::Show()
{
	for (int i = 0; i < this->vexnum; i++)
	{
		for (int j = 0; j < this->vexnum; j++)
		{
			cout << setw(4) << this->arcs[i][j] << " ";
		}
		cout << endl;
	}
}
void Graph::Create()
{
	cout << "请输入总结点数和总边数:";
	cin >> this->vexnum >> this->arcnum;//输入总顶点数和总边数
	cout << "请输入各结点的信息:";
	for (int i = 0; i < this->vexnum; i++)
	{
		cin >> this->vexs[i];
	}
	//初始化邻接矩阵
	for (int i = 0; i < this->vexnum; i++)
	{
		for (int j = 0; j < this->vexnum; j++)
		{
			this->arcs[i][j] = MAX;
		}
	}
	//构造邻接矩阵
	for (int i = 0; i < this->arcnum; i++)
	{
		int v1, v2, w;
		cout << "请输入第" << i + 1 << "条边的起点和终点及其对应的权值:";
		cin >> v1 >> v2 >> w;
		int m = LocateVex(v1);
		int n = LocateVex(v2);
		this->arcs[m][n] = w;
	}
	return;
}
void Graph::Dijkstra(VertexType start_point)
{
	//初始化最短距离数组
	for (int i = 0; i < this->vexnum; i++)
	{
		this->dist[i] = MAX;
	}
	dist[this->LocateVex(start_point)] = 0;
	//初始化保存路径的向量
	queue<VertexType>temp;
	temp.push(start_point);
	for (int i = 0; i < this->vexnum; i++)
	{
		//（移到for外）queuetemp;
		//temp.push(start_point);
		path.push_back(temp);
		//（不可行）path[i].push(start_point);//将起点作为最初始的路径加入每个结点对应的队列中
	}
	//初始化solved数组
	for (int i = 0; i < this->vexnum; i++)
	{
		solved[i] = false;
	}
	for (int i = 0; i < this->vexnum; i++)
	{
		if (this->arcs[this->LocateVex(start_point)][i] != MAX)
		{
			dist[i] = this->arcs[this->LocateVex(start_point)][i];
			path[i].push(this->vexs[i]);
		}
	}
	solved[this->LocateVex(start_point)] = true;
	for (int i = 0; i < this->vexnum; i++)
	{//返回地找
		ArcType mind = MAX;
		int v = i;
		for (int j = 0; j < this->vexnum; j++)
		{//一个劲地往前走
			//（移出for）int v = i;
			if (!solved[j] && dist[j] < mind)
			{
				mind = dist[j];
				v = j;
			}
			solved[v] = true;
			int w = this->firstadj(v);
			while (w != -1)
			{
				if (dist[v] + this->arcs[v][w] < dist[w])
				{
					dist[w] = dist[v] + this->arcs[v][w];
					path[w] = path[v];
					path[w].push(vexs[w]);
				}
				w = this->nextadj(v, w);
			}
		}
	}
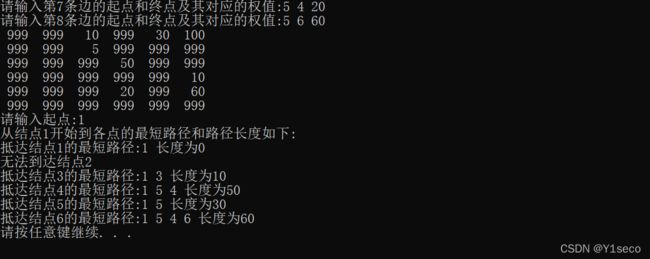
	cout << "从结点" << start_point << "开始到各点的最短路径和路径长度如下:"<<endl;
	for (int i = 0; i < this->vexnum; i++)
	{
		if (dist[i] == MAX)
		{
			cout << "无法到达结点" << this->vexs[i] << endl;
		}
		else
		{
			cout << "抵达结点" << this->vexs[i] << "的最短路径:";
			int path_length = path[i].size();
			for (int j = 0; j < path_length; j++)
			{
				cout << path[i].front() << " ";
				path[i].pop();
			}
			cout << "长度为" << dist[i] << endl;
		}
	}
}
int main()
{
	Graph s;
	s.Create();
	s.Show();
	VertexType start_point;
	cout << "请输入起点:";
	cin >> start_point;
	s.Dijkstra(start_point);
	system("pause");
	return 0;
}

结果:

参考文章

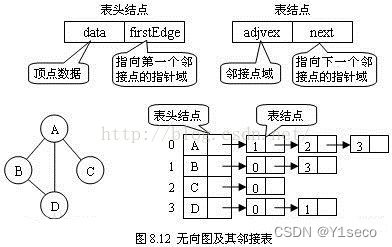
邻接表实现

待定

Floyd算法(求多源最短路径问题)

算法思想

概括为迭代更新i经由k到j的最短路径.

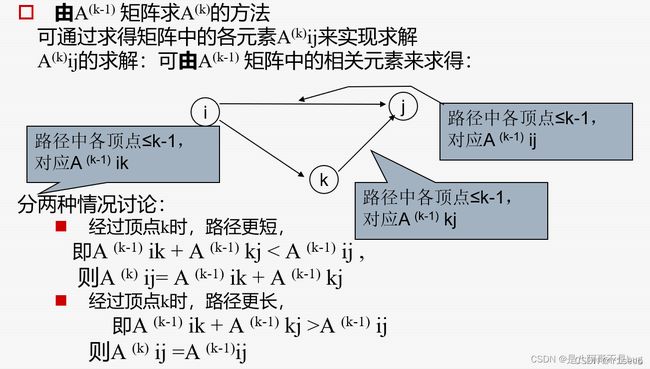
算法原理

1. 从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。
2. 对于每一对顶点 u 和v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。
3. 把图用邻接矩阵G表示出来，如果从Vi到Vj有路可达，则G[i][j]=d，d表示该路的长度；否则G[i][j]=无穷大。定义一个矩阵D用来记录所插入点的信息，D[i][j]表示从Vi到Vj需要经过的点，初始化D[i][j]=j。把各个顶点插入图中，比较插点后的距离与原来的距离，G[i][j]= min( G[i][j], G[i][k]+G[k][j] )，如果G[i][j]的值变小，则D[i][j]=k。在G中包含有两点之间最短道路的信息，而在D中则包含了最短通路径的信息。
4. 比如，要寻找从V5到V1的路径。根据D，假如D(5,1)=3则说明从V5到V1经过V3，路径为{V5,V3,V1}，如果D(5,3)=3，说明V5与V3直接相连，如果D(3,1)=1，说明V3与V1直接相连。

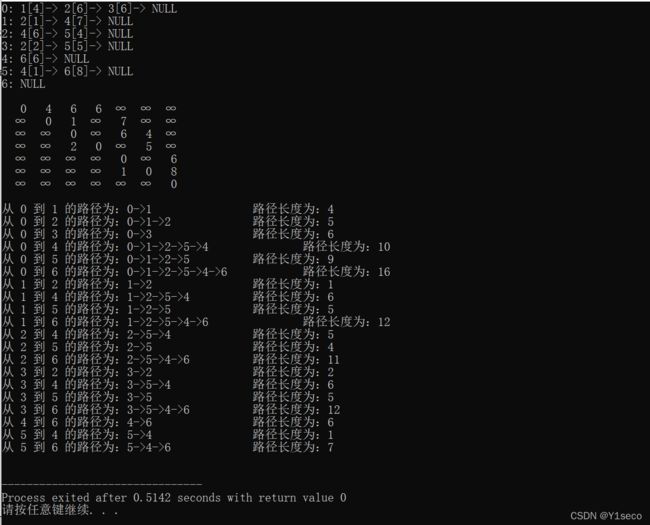
邻接矩阵实现

#include
#include

#define MAXV 7					//最大顶点个数 
#define INF 32767				//定义 ∞
//∞ == 32767 ,int 型的最大范围（2位）= 2^(2*8-1)，TC告诉我们int占用2个字节，而VC和LGCC告诉我们int占用4个字节
//图：Graph
//顶点：Vertex
//邻接：Adjacency
//矩阵：Matrix
//表：List
//边：Edge 

typedef struct vertex {
	int number;					//顶点的编号 	
}VertexType; 					//别名，顶点的类型 

typedef struct matrix {
	int n;						//顶点个数
	int e;						//边数 
	int adjMat[MAXV][MAXV];		//邻接矩阵数组			
	VertexType ver[MAXV];		//存放顶点信息 
}MatGraph;						//别名，完整的图邻接矩阵类型

typedef struct eNode {
	int adjVer;					//该边的邻接点编号 
	int weiLGht;				//该边的的信息，如权值 
	struct eNode* nextEdLGe;	//指向下一条边的指针 
}EdgeNode; 						//别名，边结点的类型 

typedef struct vNode {
	EdgeNode* firstEdLGe;		//指向第一个边结点 
}VNode; 						//别名，邻接表的头结点类型 

typedef struct list {
	int n;						//顶点个数
	int e;						//边数
	VNode adjList[MAXV];		//邻接表的头结点数组 
}ListGraph;						//别名，完整的图邻接表类型 

//创建图的邻接表 
void createAdjListGraph(ListGraph*& LG, int A[MAXV][MAXV], int n, int e) {
	int i, j;
	EdgeNode* p;
	LG = (ListGraph*)malloc(sizeof(ListGraph));
	for (i = 0; i < n; i++) {
		LG->adjList[i].firstEdLGe = NULL;						//给邻接表中所有头结点指针域置初值 
	}
	for (i = 0; i < n; i++) {									//检查邻接矩阵中的每个元素 
		for (j = n - 1; j >= 0; j--) {
			if (A[i][j] != 0) {									//存在一条边 
				p = (EdgeNode*)malloc(sizeof(EdgeNode));		//申请一个结点内存
				p->adjVer = j;									//存放邻接点 
				p->weiLGht = A[i][j];							//存放权值
				p->nextEdLGe = NULL;

				p->nextEdLGe = LG->adjList[i].firstEdLGe;		//头插法 
				LG->adjList[i].firstEdLGe = p;
			}
		}
	}
	LG->n = n;
	LG->e = e;
}

//输出邻接表 
void displayAdjList(ListGraph* LG) {
	int i;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++) {
		p = LG->adjList[i].firstEdLGe;
		printf("%d:", i);
		while (p != NULL) {
			if (p->weiLGht != 32767) {
				printf("%2d[%d]->", p->adjVer, p->weiLGht);
			}
			p = p->nextEdLGe;
		}
		printf(" NULL\n");
	}
}

//输出邻接矩阵
void displayAdjMat(MatGraph MG) {
	int i, j;
	for (i = 0; i < MAXV; i++) {
		for (j = 0; j < MAXV; j++) {
			if (MG.adjMat[i][j] == 0) {
				printf("%4s", "0");
			}
			else if (MG.adjMat[i][j] == 32767) {
				printf("%4s", "∞");
			}
			else {
				printf("%4d", MG.adjMat[i][j]);
			}
		}
		printf("\n");
	}
}

//邻接表转换为邻接矩阵
void ListToMat(ListGraph* LG, MatGraph& MG) {
	int i, j;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++) {
		for (j = 0; j < MAXV; j++) {
			MG.adjMat[i][j] = 0;
		}
	}
	for (i = 0; i < LG->n; i++) {
		p = LG->adjList[i].firstEdLGe;
		while (p != NULL) {
			MG.adjMat[i][p->adjVer] = p->weiLGht;
			p = p->nextEdLGe;
		}
	}
	MG.n = LG->n;
	MG.e = LG->e;
}

//输出多源最短路径
void displayPath(MatGraph MG, int A[MAXV][MAXV], int path[MAXV][MAXV]) {
	int i, j, k;
	int s;
	int aPath[MAXV];										//存放一条最短路径（逆向）
	int d;													//顶点个数
	for (i = 0; i < MG.n; i++) {
		for (j = 0; j < MG.n; j++) {
			if (A[i][j] != INF && i != j) {					//若顶点 i 和 顶点 j 之间存在路径
				printf("从 %d 到 %d 的路径为：", i, j);
				k = path[i][j];
				d = 0;
				aPath[d] = j;								//路径上添加终点
				while (k != -1 && k != i) {					//路劲上添加中间点
					d++;
					aPath[d] = k;
					k = path[i][k];
				}
				d++;
				aPath[d] = i;								//路径上添加起点
				printf("%d", aPath[d]);						//输出起点
				for (s = d - 1; s >= 0; s--) {				//输出路径上其他顶点
					printf("->%d", aPath[s]);
				}
				printf("\t\t");
				printf("路径长度为：%d\n", A[i][j]);
			}
		}
	}
}

//Floyd算法
void Floyd(MatGraph MG) {
	int i, j, k;
	int A[MAXV][MAXV];
	int path[MAXV][MAXV];
	for (i = 0; i < MG.n; i++) {
		for (j = 0; j < MG.n; j++) {
			A[i][j] = MG.adjMat[i][j];
			if (i != j && MG.adjMat[i][j] < INF) {
				path[i][j] = i;							//顶点 i 到顶点 j 有边时
			}
			else {
				path[i][j] = -1;						//顶点 i 到顶点 j 无边时
			}
		}
	}
	for (k = 0; k < MG.n; k++) {						//一次考察所有顶点
		for (i = 0; i < MG.n; i++) {
			for (j = 0; j < MG.n; j++) {
				if (A[i][j] > A[i][k] + A[k][j]) {
					A[i][j] = A[i][k] + A[k][j];		//修改最短路径长度
					path[i][j] = path[k][j];			//修改最短路径
				}
			}
		}
	}
	displayPath(MG, A, path);							//输出最短路径
}

int main() {
	ListGraph* LG;
	MatGraph MG;

	int array[MAXV][MAXV] = {
		{  0,  4,  6,  6,INF,INF,INF},
		{INF,  0,  1,INF,  7,INF,INF},
		{INF,INF,  0,INF,  6,  4,INF},
		{INF,INF,  2,  0,INF,  5,INF},
		{INF,INF,INF,INF,  0,INF,  6},
		{INF,INF,INF,INF,  1,  0,  8},
		{INF,INF,INF,INF,INF,INF,  0}
	};

	int e = 12;
	createAdjListGraph(LG, array, MAXV, e);
	displayAdjList(LG);
	printf("\n");

	ListToMat(LG, MG);
	displayAdjMat(MG);
	printf("\n");

	Floyd(MG);
	printf("\n");

	return 0;
}

结果:

参考文章1
参考文章2

拓扑排序

原理

1. 从AOV网中选择一个没有前驱的顶点并输出.
2. 从网中删除该顶点和所有以它为起点的有向边.
3. 重复直至AOV网为空或当前网中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环.

栈实现拓扑排序（邻接表实现）

#include 
#include 
#include 
#include 
using namespace std;

#define MAX_VERTEX_NUM 26

typedef struct ArcNode {
	int adjvex;
	struct ArcNode *nextarc;
	ArcNode() {
		nextarc = NULL;
	}
} ArcNode; //结点

typedef struct VNode {
	int data;
	ArcNode *firstarc;
	VNode() {
		firstarc = NULL;
	}
} VNode, AdjList[MAX_VERTEX_NUM];

typedef struct {
	AdjList vertices;
	int vexnum, arcnum;
} ALGraph;

bool TopologicalSort(ALGraph G, int *indegree) {
	stack<int> s;	//初始化栈

	int i, k;
	for (i = 1; i < G.vexnum + 1; i++) {
		if (!indegree[i])
			s.push(i); 	//入度为0的顶点入栈
	}

	int count = 0;	//记录当前已经输出的顶点数
	ArcNode *p;
	while (!s.empty()) {
		i = s.top();
		s.pop();
		cout << G.vertices[i].data << "->";
		count++;
		for (p = G.vertices[i].firstarc; p; p = p->nextarc) {
			k = p->adjvex;
			indegree[k]--; //将所有指向i的顶点的入度减一，并且将入度为0的顶点压入栈s
			if (!indegree[k])
				s.push(k);
		}
	}

	if (count < G.vexnum)
		return false;

	return true;
}

int main() {
	int i;
	ALGraph g;
	cout << "载入图中..." << endl;
	ifstream fin("in.txt");
	fin >> g.vexnum >> g.arcnum;
	for (i = 1; i < g.vexnum + 1; i++)
		g.vertices[i].data = i;

	int b, e;
	ArcNode *p;
	int *indegree = new int[g.vexnum + 1];
	//注意 int *a=new int(n);  申请一个整型变量空间，赋初值为n，并定义一个整型指针a指向该地址空间
	//int *indegree=(int *)malloc(sizeof(int)*(g.vexnum+1));
	memset(indegree, 0, sizeof(int) * (g.vexnum + 1));
	for (i = 1; i < g.arcnum + 1; i++) {
		fin >> b >> e;
		cout << "第" << i << "条边：" << b << "->" << e << endl;

		p = new ArcNode();
		p->adjvex = e;
		p->nextarc = g.vertices[b].firstarc;
		g.vertices[b].firstarc = p;
		indegree[e]++;
	}

	if (TopologicalSort(g, indegree))
		cout << "正常完成！" << endl;
	else
		cout << "该有向图有回路！" << endl;

	return 0;
}

测试数据,新建in.txt文件输入内容

1）有环
4 4
1 2
2 3
3 4
4 2

2）无环
12 16
1 2
1 3
2 3
1 4
3 5
4 5
11 6
5 7
3 7
3 8
6 8
9 10
9 11
9 12
10 12
1 12

结果:

参考文章
https://cloud.tencent.com/developer/article/1569368