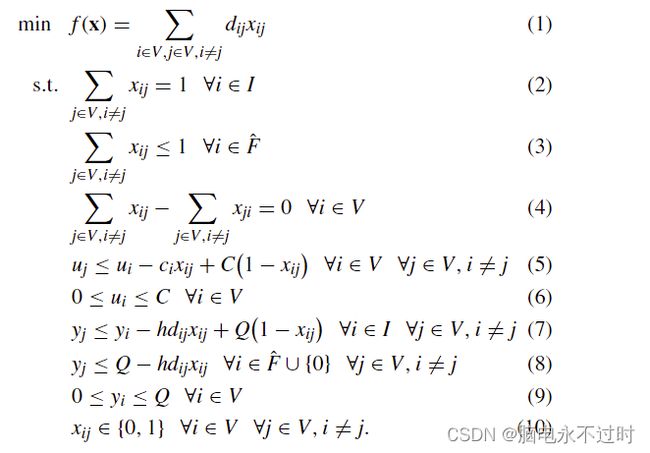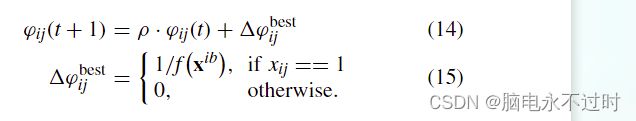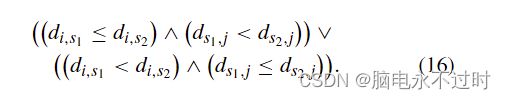电容式电动汽车路径规划问题的双级蚁群优化算法

摘要：

        电动汽车（EV）技术的发展导致了一个新的车辆路由问题（VRP），称为有容量的电动汽车路由问题（CEVRP）。由于充电站的数量有限，电动汽车的巡航范围有限，不仅要考虑客户的服务顺序，还要考虑电动汽车的充电时间表。然而，将问题的这两个方面放在一起解决是非常困难的。为了解决上述问题，我们将CEVRP视为一个二层优化问题，并在本文中提出了一种新颖的二层蚁群优化算法，该算法将CEVRP分为两个层次的子问题：1）有容量的VRP和2）固定路线车辆充电问题。对于上层子问题，电力约束被忽略了，并设计了一个顺序第一的分割第二的最大蚁群系统算法来生成满足客户需求的路线。对于下层子问题，设计了一个新的有效启发式方法来决定生成路线的充电时间表，以满足电力约束。由此产生的解决方案的目标值被用来更新上层蚁群系统算法的信息素信息。通过对这两个部分的良好协调，所提出的算法可以在广泛的基准实例上大大超过最先进的算法。

引言

        几十年来，运输一直是温室气体排放的主要来源之一[1]。最近，电动汽车的快速发展为传统化石燃料汽车提供了一种适用的替代方案[2]，[3]。根据[4]，用电动汽车取代传统汽车可以大大减少温室气体排放。考虑到日益严重的环境问题和政府政策[5]，许多物流公司，如DHL、京东和联邦快递，已经开始在其快递业务中使用电动汽车，而不是传统的化石燃料汽车。

        从学术角度来看，物流公司提供的服务通常被建模为车辆路由问题（VRPs）。在过去的几十年里，有许多不同的VRP变体被广泛研究[8]，如电容式VRP（CVRP）[13]，[14]；带时间窗口的VRP[9]，[15]；带取货和送货的VRP[12]；多目标VRP[16]，[17]；和动态VRP[10]。这些变体大多是基于传统车辆建立的。由于传统车辆的巡航范围相当长，而且加油站在现代城市中很普遍，所以在这些传统的VRP中通常不考虑加油问题。然而，电动车的巡航范围还不能与传统车辆相提并论，即使在一个城市的城市地区，目前也没有很多充电站[18]。这些问题使得管理电动车队比传统车辆更难，导致了一类新的VRP，称为电动VRP（EVRP）[19]。在EVRP中，应该考虑两个方面。1）客户的服务顺序和2）每辆车的充电时间表。由于这两个方面是高度相互依赖的，大多数现有的传统VRP的方法不能直接应用于EVRP。

        EVRP是一个全新的课题。现有的大多数研究都集中在提出和定义新的问题模型上，例如容量EVRP（CEVRP）[6]；带时间窗口的EVRP（EVRPTW）[19]，[20]；带收货和交付的EVRP[21]；具有非线性充电的EVRP[22]；以及具有共享充电站的EVRP（EVRP SCS）[23]。与所提出的问题相比，在设计算法上花费的精力相对较少。因此，这些问题大多没有得到广泛的研究。纵观VRP的研究历史，我们知道对基本CVRP的充分研究将对其他变体大有裨益。遵循同样的路径，本文将CEVRP作为EVRP的基本模型进行研究，为EVRP的基础研究做出贡献[6]。继传统CVRP的定义之后，CEVRP的目标也被定义为电动汽车总行驶距离的最小化。电动汽车从停车场出发为客户服务。每个客户都应该得到一次服务。每辆电动汽车在行驶过程中都不能超载或电量耗尽。如果车辆仅使用初始电力无法完成旅程，则可以在充电站为电池充电。在为所有客户提供服务后，所有电动汽车都应返回停车场。

        到目前为止，大多数现有的解决EVRP的方法都分为两类。在第一类中，学者们将EVRPs转移到混合整数线性规划/（MILP）问题中，并应用CPLEX[24]等商业软件来解决这些问题[25], [26]。商业软件在小规模的问题上可以产生非常好的解决方案，但高计算复杂性使得它们在超过50个客户的大型问题上效率很低[22]。基于个体的元启发式算法[27]是第二类算法，包括可变邻域搜索（VNS）[20]；迭代局部搜索（ILS）[28]，[29]；以及自适应大邻域搜索（ALNS）[30]，[31]。这些算法可以是有效的，但最终解决方案的质量高度依赖于扰动和应用的局部搜索算子。另外，由于只有一个正在运行的解决方案，这些算法对初始解决方案的质量很敏感。如果应用的算子不合适或者初始解不好，算法很容易陷入糟糕的局部最优状态[27]。

        蚁群优化（ACO）算法已被证明对许多路由问题有效，如旅行推销员问题（TSP）[32]，[33]；VRPs[34]；和弧形路由问题（ARPs）[35]。作为一种基于种群的元启发式算法，ACO比基于个体的元启发式算法具有更好的适应性，因为它不依赖于特定的扰动或局部搜索算子，而且它对初始解不那么敏感[36], [37]。在几个ACO变体[38]中[40]，本文采用了最大值蚁群系统（MMAS），因为它比其他系统有更好的能力[36]。

        然而，直接使用MMAS来生成一个包含CEVRP的服务订单和充电时间表的综合解决方案是很困难的。Guo等人[41]和Shao等人[42]试图通过在他们的遗传算法（GA）中一起编码客户订单和充电站订单来同时解决EVRP的两个方面。然而，这种编码方案导致了巨大的搜索空间，而且传统的局部搜索方法如2-opt也不能应用，因为它们不能处理有充电站的路线。这些缺点使得所提出的GA在大规模EVRP上没有效果。

考虑到这些缺点，我们在本文中以二层优化的方式解决CEVRP。主要贡献如下：

1）通过考虑CEVRP作为一个二层优化问题，设计了一个二层ACO（BACO），以减少搜索空间，并更多地关注有希望的区域。这两个层次的子问题是CVRP和固定路线车辆充电问题（FRVCP）fixed route vehicle charging problem ，对应于客户的服务顺序和车辆的充电时间表。

2）提出了一种顺序第一、分割第二的MMAS（OS-MMAS）算法，为上层子问题CVRP生成容量可行的路线，决定客户的服务顺序。

3) 设计了一种新的启发式方法，称为移除启发式（RH），以解决较低级别的子问题FRVCP，决定车辆的充电计划。插入充电站后集成解决方案的适应度值将用于更新OS-MMAS的信息素信息。此外，在RH的基础上，进一步提出了一种限制枚举方法来细化最终解决方案的充电时间表。

        本文的其余部分组织如下。第二节给出了CEVRP的正式描述。然后，第三节展示了相关的工作。第四节解释了拟议的算法BACO。最后，第五节进行了实验研究，第六节得出结论。

II.问题定义

        给定一个同质电动车车队，CEVRP的目标是找到一个最佳路线集，在几个约束条件下使总行驶距离最小。CEVRP可以正式定义在一个全连接的加权无向图G = (V , E ).V ={ 0}∪I∪ˆF代表图中的节点集合。0是仓库的索引。I代表客户。每个客户都有一个固定的货物需求 c i 。ˆ F是一个扩展的充电站集合，包含每个充电站i∈F的β i份。创建充电站的副本允许每个充电站被多次访问[43]。β ii设置为2 |I |，因为在最坏的情况下，每辆电动车需要在为客户提供服务和返回仓库的两种方式中访问每个站点一次[44]。E ={ (i , j )|i , j∈V , i = j }是弧的集合。每个弧（i , j ）都与一个代表i和j之间距离的权重有关，表示为d ij。每辆电动车都有最大容量的货物需求C和最大电池容量Q。电池的消耗率表示为h。对于每个弧（i , j ），电动车将消耗电池的数量h - d ij来穿越它。通过引入另外两个变量u i和y i，分别代表电动车到达节点i∈V时的剩余承载能力和剩余电池水平，CEVRP的数学定义在[6]中给出如下。

        该问题的目标（1）是最小化所有电动汽车的总行驶距离。约束条件（2）规定每个客户只能得到一次服务。约束（3）指示充电站可以被访问多次。约束条件（4）保证每辆电动汽车都必须离开为其服务的每一位客户。约束条件（5）和（6）规定电动汽车在行驶过程中不能超载。在本文中，我们将这种约束称为“容量约束”。约束条件（7）-（9）规定，电动汽车在行驶过程中不会耗尽电力。相应地，我们将这个约束称为“电约束”。约束（10）定义了xij的域。如果电弧（i，j）由EV行进，则x ij等于1，否则，它等于0。尽管公式显示了明确的限制，但公式也暗示所有电动汽车都应该离开并返回停车场。此外，约束条件（7）-（9）假设电动汽车总是在充电站充满电。需要注意的是，本文中研究的CEVRP正是[6]中提出的EVRP，但是，为了符合传统VRP的命名法，在表示容量约束的名称中添加了“capitated”一词。图1显示了一个由两条路线组成的示例。一辆电动汽车在行驶过程中两次访问充电站，另一辆电动车辆没有访问任何充电站。

---

 III.相关工作

        在这一节中，回顾了为解决EVRPs而提出的方法。EVRP的前身是绿色VRP（GVRP）[43]，它是一个替代燃料车辆的路由模型。在GVRP的基础上，运筹学界和交通研究界的学者们用电动汽车取代了替代燃料汽车，开始研究EVRP。

        处理EVRP的一种流行方法是将EVRP建模为MILP问题，并使用商业软件（如CPLEX和Gurobi）来解决这些问题。林等人[25]使用CPLEX解决了车辆负载对能耗影响的EVRP。目标是最大限度地减少送货的总成本，包括司机的小时工资和收费成本。测试了一个仅包含13个客户的场景。Montoya等人[22]提出了一种称为EVRP的非线性充电变体，该变体采用了不同类型的充电站。此外，充电过程被建模为一个非线性函数。他们试图使用Gurobi来解决问题，但发现它只能在给定的时间内解决少于50名客户的问题。Chen等人[21]提出了一个带取送的EVRP的混合整数二次约束规划模型，并使用CPLEX来解决该问题，但测试用例只考虑了不到20个客户。肖等人[45]专注于将能源消耗模型开发为EVRPTW，以最大限度地降低总成本，如[25]。此外，实验表明，在给定的时间内，CPLEX只能解决客户少于30个的情况。尽管使用数学规划方法解决问题是获得高质量解决方案的简单方法，但文献中的实验表明，由于时间复杂性高，这些方法不足以解决50多个客户的问题。

        基于个体的元启发式算法也被广泛用于解决EVRP，如VNS、ILS和ALNS。VNS是第一个应用于EVRP的系统。2014年，Afroditi等人[19]和Schneider等人[20]都提出了他们的EVRPTW模型。Schneider等人提出了一种带有禁忌搜索方法的VNS启发式方法来解决这个问题。根据他们的研究，Bruglieri等人[46]，[47]将EVRPTW的目标从总行进距离改为总时间。他们将VNS与局部分支方法相结合来解决这个问题。最近，Mavrovouniotis等人[6]提出了一种VNS算法，该算法赢得了IEEE WCCI2020关于EVRP的EC竞赛。关于ILS，张等人[29]通过考虑许多因素对电动汽车的能耗进行了建模，并提出了一种使用ACO作为扰动算子的ILS算法来解决该问题。一般来说，ACO被认为是一种基于群体的元启发式算法，但在他们的算法中，只有一只蚂蚁。因此，它仍然是一种基于个体的算法，而不是基于群体的算法。除了使用Gurobi，Montoya等人[22]还提出了一种ILS算法来解决具有非线性充电的EVRP。根据Montoya的工作，Froger等人[44]进一步改进了FRVCP的模型和启发式算法，但仍然使用了以前ILS算法生成的相同路线。ALNS是另一种流行的基于个体的元启发式算法。Keskin和Çatay[31]，[48]通过考虑部分充电情况和不同的目标，提出了他们的EVRPTW模型。两个工作都应用了相同的ALNS算法。Koç等人[23]考虑了几家公司联合投资充电站的情况，并提出了EVRP SCS问题。EVRP-SCS不仅包括电动汽车的路由，还包括充电站的定位。他们使用ALNS和CPLEX来解决问题的不同部分。一般来说，这些基于个体的元启发式算法通常能有效地解决问题，但其性能在很大程度上取决于所应用的扰动/破坏算子和局部搜索方法，这两种方法都与问题有关。设计这些运算符和方法需要很高的专业知识。如果应用的扰动/破坏算子和局部搜索方法不合适，该算法将经常遇到过早收敛问题，尤其是对于大型复杂问题[27]。此外，初始解的质量对应该谨慎生成的最终解有很大影响。

        考虑到进化计算的良好适应性，一些学者也尝试使用进化计算算法来求解EVRP。刘等人[49]提出了一种差分进化算法来解决电动汽车充电调度问题，但与以往的工作不同，它主要关注电动汽车点到点的充电调度，而不是为一组客户服务。郭等人[41]和邵等人[42]提出了两种GA来解决EVRPTW。为了同时决定客户订单和充电订单，郭等人将客户和站点编码在GA中，并做出了一个不切实际的假设，即每个站点只能访问一次。这种假设使得该算法仅适用于一些特定的小规模问题。Shao等人通过为每个站点设置副本来解决这个问题，但这种行为导致了另一个巨大而冗余的搜索空间的严重问题。

        总的来说，我们发现最先进的EVRPs方法仍有局限性。目前，这些数学方法的效率不足以解决超过50个客户的EVRPs。如果不精心设计扰动/破坏算子、局部搜索方法和初始解生成方法，基于个体的元启发式算法很容易陷入局部优化。演化算法没有纳入一个好的方法来同时处理客户和充电序列。考虑到这些缺点，在这篇文章中，我们提出了一种叫做BACO的二层算法来解决CEVRP。

IV. BACO

        在这一节中，我们首先给出BACO的整体过程。然后，BACO的三个组成部分，包括。1）上层CVRP的OSMMAS；2）下层FRVRP的RH；以及3）最终的解决方案细化程序。最后，分析了该算法的理论时间复杂性和设计理念。

A.BACO的过程

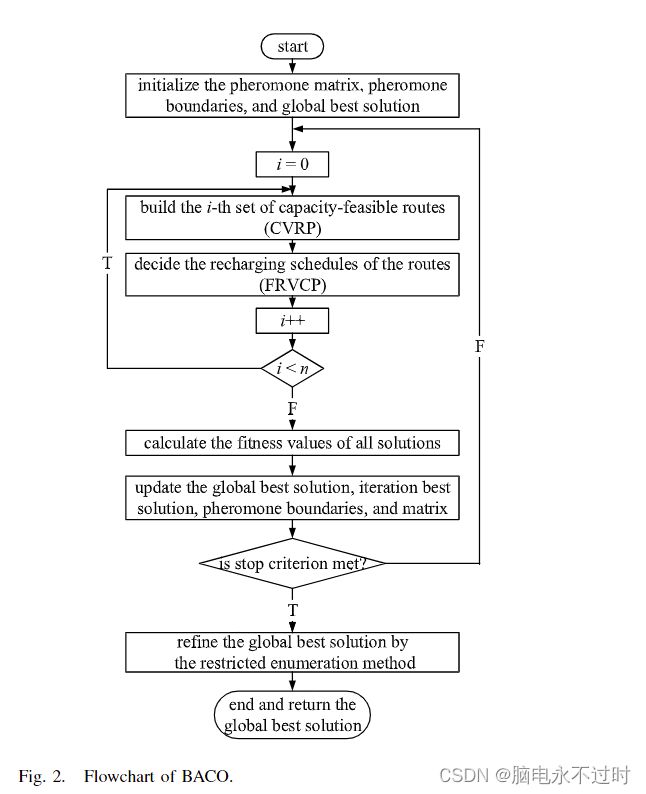
        BACO的整体过程如图2所示。如流程图所示，该算法的组成部分和参数首先被初始化。然后，在每一代中，n =| I |+1 逐一建立他们的解决方案。对生成的解决方案进行评估，以更新全局最佳解决方案、迭代最佳解决方案、信息素边界和信息素矩阵。如果满足停止标准，则对全局最佳解采用限制性枚举法进行最终细化。最后，整个算法结束并返回全局最佳解。

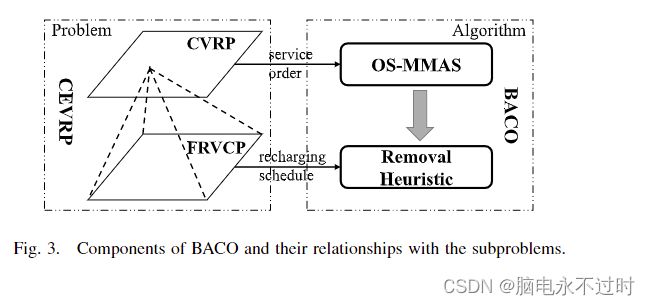
        图3展示了CEVRP的二层结构和与BACO的关系。对应于两级子问题，在BACO中需要两个步骤来生成一个可行的解决方案。首先，通过取消电力约束和充电站，CEVRP被降级为相应的CVRP。只考虑仓库和客户，OS-MMAS算法被应用于生成相应CVRP的容量可行的路线。然后，考虑到容量可行的路线，我们将电力约束考虑在内。为固定路线寻找最佳充电时间表的问题被称为FRVCP。为了有效和高效地解决FRVCP，我们提出了RH算法。

       在生成解决方案后，对目标值进行评估，以更新全局最佳解决方案和信息素图矩阵。RH是一种确定性的算法。它提供了相应CVRP的路线和CEVRP的适应度之间的单值映射关系。因此，我们可以直接使用解决方案的适应度值来更新OS-MMAS的信息素矩阵。补充材料中进一步分析了这两个子问题的表述及其与CEVRP的关系，以说明BACO如何以二层方式处理该问题。

B. 用于构建路线的OS-MMAS

        信息素设置：在OS-MMAS中，维持信息素矩阵来引导蚂蚁构建路线。首先，我们为相应的CVRP生成路线，而不考虑充电站。因此，信息素矩阵的大小是n×n，其中n=|I|+1是客户总数加上仓库。每个元素φij∈表示从i到j的信息素值。由于应用的ACO算法是MMAS[40]，因此用于保持算法探索能力的信息素值有两个边界φmin和φmax，φmin≤φij≤φmax。这两个边界的值为[40]。

其中ρ是用于控制信息素蒸发速度的参数。xgb是全局最佳解。pr是一个参数，通常被设置为0.05。在BACO中，为了生成初始的xgb ,首先应用凸壳插入法来生成一个巨大的tour。然后，这个巨大的旅游被分割成一组容量可行的路线。之后，这些路线被RH固定为一个电力可行的解决方案。初始信息素φ 0的值被设定为等于φ max的值。

路线构建：

        OSMMAS的路由构建过程如算法1所示，它可以分为两个子过程。1）顺序优先的子过程，生成一个巨大的旅行空间（第1-11行）；2）分割第二的子过程，将旅游分割成容量可行的路线（第12-30行）。

        首先，巨型旅游r被初始化为空，包含仓库和客户的集合ˆ I被初始化（第1行）。从ˆ I中随机选择一个节点作为起点。它被添加到旅游路线r中，并从ˆ I中删除（第2行第4行）。ˆ I中的剩余节点将被逐一选择，直到构建出完整的旅游路线（第5行）。在每一步中，通过轮盘选择策略从ˆ I中选择下一个节点j（第7行）。从当前节点i到j的概率为[40] ：

 

         其中α和β是两个参数，用于平衡信息素值和距离值之间的重要性。从（13）中，我们可以知道，信息素值较大、与ii的距离较短的节点是首选。之后，这个被选中的节点j被添加到旅游路线r中，并从ˆ I中移除（第8行和第9行）。当所有客户和仓库都被选中后，我们旋转r，让仓库成为旅游中的第一个节点（第11行）。

         然后，通过使用[50]中提出的分割算法，将旅游路线r分割成几条容量可行的路线。给定一个从仓库0开始的旅游路线r，分割算法为每个节点r i保持两个值V i和P i，这两个值表示直到r i为止的所有生成路线的最小总距离及其在路线（线12）中的前一个的索引。通过两个嵌套的循环（第13-29），该算法为每个节点找到导致最小整体距离的前任，该距离等于V |I |。然后，从r中的最后一个节点开始，所有的路由都可以通过回溯过程生成（第30行）。从本质上讲，分割算法列举了所有容量可行的路线，并找到了巨型旅游的最佳分割。在生成所有路线后，2-opt算法被用作每条路线的局部搜索方法，以进一步改善解决方案（第31行）。

        信息素更新。在获得路线集后，将确定路线的充电时间表，以获得原始CEVRP的可行解决方案。后面将介绍在路线中插入充电站的过程。在每个迭代结束时，这些可行的解决方案将被评估。迭代的最佳解决方案xib和相应的巨型旅游肋骨被记录下来。如果迭代best xib优于全局best xgb ,xgb将被更新。φ max和φ min也将根据（11）和（12）进行更新。信息素矩阵根据更新 (14)：

 C.固定路线车辆充电的移除启发式 RH

         在路线建设之后，有些路线是不可行的。我们需要在这些路线中插入充电站，使其在电力上可行。为此，我们提出了一种新的启发式算法，称为RH，以解决下层子问题FRVCP，如算法2所示。它可以分为两个阶段。1）插入（第1-6行）和2）删除（第7-3行）。

        在插入阶段，在每对连续节点Γi和Γi+1之间，找到并插入一个带来最小额外行进距离的站点s（第2–6行）。考虑了电力约束，使得在插入阶段（第3行）之后得到的路线Γ是电力可行的。

        然后，在移除阶段，我们逐个移除多余的站点。对于Γ（9行）中的每个站s，我们首先判断Γ在去除s（11行）后是否仍然是电可行的。如果它可以在不违反电力限制的情况下拆除，我们将记录拆除该站（12-15行）所节省的距离。在检查了所有车站后，可以合法拆除并带来最大距离节省的车站被拆除（18行和19行）。如果没有可以移除的站点，则整个过程停止并返回电力可行路线Γ。

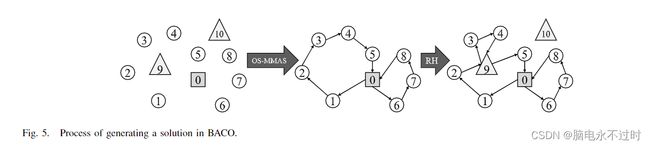
        图4中显示了n个例子来证明RH。给定一条路线（0, 1, 2, 3, 5, 0），在插入阶段，RH首先在每对连续节点之间的路线上插入五个充电站（6 , 7 , 7 , 8 , 9 ）。然后，在删除阶段，删除三个车站，只保留两个车站。

D.限制性列举法 RE

        由于FRVCP也是一个NP难题[22]，因此枚举所有充电计划的成本太高。作为一种启发式方法，RH是有效的，但不能保证最优的充电计划。为了进一步改进最终的全局最优解，我们在RH获得的解的基础上设计了一种受限枚举方法。具体而言，对于每条路线，可以合理地考虑，最优解决方案往往不会比RH获得的解决方案有更多的充电站访问，因为更多的访问往往会导致额外的成本。因此，限制枚举方法只检查与RH获得的解决方案相比没有更多充电站的解决方案。给定任意一对节点i和j，我们可以进一步过滤掉一些显然没有被最优解考虑的充电站。借用多目标优化的概念，我们将两个站点之间的“优势”关系定义如下。

定义1：给定两个节点i和j，当且仅当时，一个站s 1被称为支配另一个站s 2。

        基于支配关系，我们只需要考虑i和j之间的非支配站。根据上述分析，算法3中给出了限制性枚举算法。

​​​​​​​ 

        首先，采取由RH产生的电力可行路线Γ，我们计算Γ中有多少个站点，表示为ub（第1行）。然后，找到每对连续的节点Γ i和Γ i +1之间的非支配站并存储在Π i中（第3行）。在得到上界和非支配站列表后，我们使用函数enumerate (Γ ′ , sn , )来列举所有可能的包含从（第7行和第8行）选择的sn充电站的充电时间表。每当找到一个更好的解决方案 ， Γ 就会被更新 （ 第 9 行第 11 行 ） 。由于篇幅所限，关于函数enumerate的详细伪代码在补充材料中给出。

E.讨论

 1）时间复杂度分析。BACO的时间复杂度是以自上而下的方式分析的。首先，整个算法的复杂度可以显示为O (X - N gen + Y )，其中N gen,O (X )和O (Y )分别代表代数、一代的时间复杂度和限制性枚举方法的时间复杂度。

        从图2我们可以知道，每一代BACO有三个操作：1）生成n组可容路由；2） 决定这些路线的再充电时间表；以及3）更新信息素矩阵。第一次运算的时间复杂度为O（n·（n2+q·n）），其中O（n2）是生成一个巨大旅行的时间复杂程度，O（q·n）是分裂的复杂程度[50]，q=C/（∑i∈Ic i/|i|）。对于第二次运算，假设有m=|F|个站（在我们的算法中不考虑这些站的副本），时间复杂度为O（n·（m·n+n2）），其中O（m·n+n2）是RH的时间复杂度。第三个运算的时间复杂度是O（n2）。将这三个分量加在一起，我们可以得到O（X）=O（n2·（2n+q+m+1））。

        因此，在最坏的情况下，限制性列举方法仍然需要列举所有可能的解决方案，其理论上的时间复杂度为O((m - n )n)，非常高。然而，实际上，车辆在行驶过程中只会给电池充电少于5次，而且两个连续的客户之间的非主导充电站数量通常小于或等于3个。因此，限制性枚举方法的实时复杂度小于O（Y）=O（（3n）4）。

        总的来说，BACO的时间复杂度是O (n2 - (2n + q + m +1 )-N gen+(3n )4 ) = O (n2 -(n +q +m )-N gen+n4 )。由于在大多数情况下q n和m n，BACO的时间复杂度大约是O（n3 - N gen + n4）。

2）设计理念。

        BACO的基本设计理念是分而治之，这导致了图5显示中的二层结构。BACO将CEVRP分为两个子问题，即CVRP和FRVCP，它们都是NP-hard[22]。在BACO中，客户的服务顺序由OS-MMAS产生，充电时间表由RH产生。我们以这种方式设计BACO有两个原因。

         1）如果应用元启发式算法来解决FRVCP，将有两个元启发式算法对应于两个层次的优化，这将导致极高的时间复杂性。许多研究表明，不仅对于EVRP[22]，而且对于其他一些组合优化问题[51]，[52]，在这两个层面上使用元启发式算法的计算成本太高。

        2）尽管CVRP和FRVCP都是NP-hard问题，但CVRP的高质量路线集是FRVCP成功的前提条件。另外，客户的数量通常大于充电站的数量，这意味着CVRP的复杂性高于FRVCP的复杂性。因此，我们选择使用元启发式算法来解决CVRP，并使用启发式算法来解决FRVCP。

        BACO的设计理念并不意味着FRVCP并不重要。为了得到CEVRP的良好解决方案，CVRP和FRVCP都应该被成功解决。

        一般来说，通过体现分而治之的策略，BACO成功地将CEVRP的搜索空间分解为两个子空间。对于每一级的优化，搜索空间都会减少，而不会损失很多有用的信息，这使得找到一个好的解决方案比直接在整个空间搜索更容易。考虑到这两个子问题的复杂性，元启发式算法OS-MMAS被用来生成客户的良好服务订单，并定义了下层搜索空间的有希望的区域。启发式算法RH决定了每辆车的充电时间表，这有助于BACO在不具有高计算复杂性的情况下产生良好的解决方案。

---

五：实验

A.实验设置

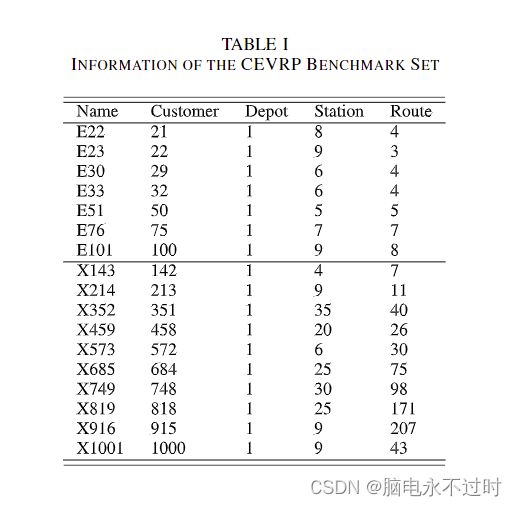
        1) 基准实例。为了研究BACO的性能，我们采用了IEEE WCCI2020EC竞赛中新提出的EVRP的基准[6]。该基准包含一组小规模的实例和一组大规模的实例。小规模组由七个实例组成，有多达100个客户。大规模组由10个实例组成，有多达1000个客户。这两个群体分别来自[53]和[54]。该基准的细节显示在表I中。

2) 算法设置。为了检查BACO的能力，我们在每个实例上设置了一个固定的执行时间，使BACO能够趋同。

        其中，对于E22-E101、X143-X916和X1001，θ分别等于1、2和3。在组合优化研究中，使用固定的执行时间作为终止条件是一种常见的方法[55]。BACO在C++中实现，并在带有Arch Linux系统的Intel i7-6700 3.40Hz CPU上执行。在每个实例上，BACO被执行30次。

        我们将BACO与五种算法进行比较，即VNS、模拟退火（SA）、GA、ILS和单级MMAS，表示为SLMMAS。前三种算法是IEEE WCCI2020EC竞赛中EVRP的获胜者[1]。 ILS最初是为了解决非线性充电的EVRP而提出的，但通过将工作时间的约束改为容量的约束，它可以很容易地用于解决CEVRP[22]。它使用顺序第一、分割第二的ILS来生成容量可行的路线，并使用贪心启发式（GH）算法来插入充电站。我们自己实现了SLMMAS，以证明BACO的二层结构的优势。SLMMAS在建设路线时插入了充电站。每当由于电力限制，下一个被选中的客户无法到达时，在为客户提供服务之前，会访问一个带来最小额外距离的充电站。由于没有提供比赛三个获奖者的代码和论文，我们直接使用报告的结果进行比较，包括最小值、平均值和标准偏差值。同时，在BACO和三种算法之间进行单样本t检验，以检查它们的性能是否有明显差异。与ILS和SLMMAS一样，它们也在每个测试案例上独立测试了30次。使用Wilcoxon秩和检验将它们的性能与BACO进行了比较。显著性水平被设定为0.05，并进行Bonferroni校正。

        BACO的所有参数都遵循MMAS[40]的规范设置。BACO的种群大小设置为n=|I|+1。信息素蒸发速度ρ设定为0.98。α和β分别设置为1和2。对于客户少于500人的实例，生成的巨型游览就像算法1一样。对于拥有500多个客户的实例，首先在初始化阶段为每个节点生成候选列表I。每个列表̄I I维护与节点I最近的20个节点。当构建巨型巡回赛时，蚂蚁会从候选列表中选择节点，而不是从通用集合中选择。这种方法在ACO算法中被广泛采用[39]，[40]。我们还研究了α和β的影响。实验结果表明，常规设置α=1，β=2是BACO的良好选择。由于篇幅限制，本实验在补充材料中提供。

B.关于小规模实例的比较

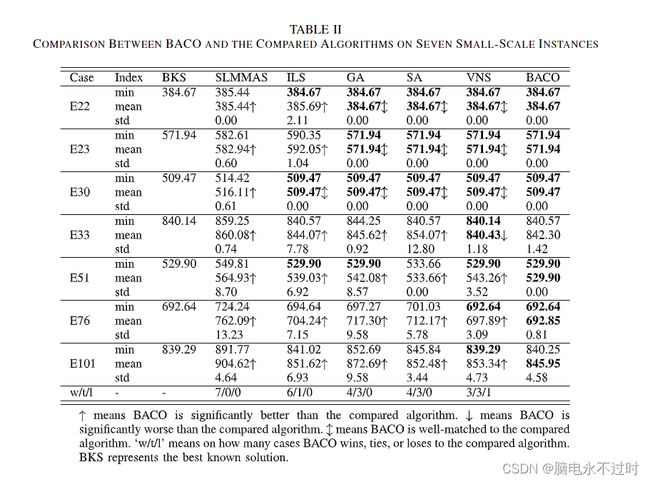
         我们首先在小规模实例上比较这些算法。实验结果显示在表二中。最好的最小值和平均值被突出显示。从结果中，我们可以得到以下信息。

1）根据统计学检验，BACO在E33上只比VNS差。在其他实例中，BACO要么具有与被比较算法相当的性能，要么明显优于其他算法。

2）根据最小目标值，VNS在所有七个实例中都找到了已知的最佳解决方案。BACO找到了7个中的5个，但在BACO失败的两个实例中找到了已知的最佳解决方案，即E33和E101，BACO和VNS找到的解决方案之间的差距非常小。

3）BACO在小规模实例上的优越性的原因是OS-MMAS和RH在小规模实例上都是有效的。OS-MMAS不依赖任何预定义的邻域结构来生成路线。对于CEVRP来说，邻域结构很难定义，因为不仅要考虑客户的服务订单，还要考虑车辆的充电时间表。使用OS-MMAS可以为RH生成许多不同的候选路线，对于小规模的实例，RH非常有效地找到最佳或接近最佳的充电时间表。相反，在基于个体的元启发式算法中使用预定义的邻域结构可能会错过一些好的解决方案。

4）与SLMMAS和GA等基于群体的元启发式算法相比，BACO的二层优化结构在有效性方面具有优势。通过分解决策空间，我们可以使用不同的有效方法来处理不同层次的子问题（OS-MMAS代表上层，RH代表下层），通过解决这两个子问题产生的综合解决方案被用作反馈，帮助OS-MMAS产生更好的客户服务订单。因此，BACO的有效性得到了一定程度的保证。然而，在SLMMAS中，由于车辆的充电时间表是随着路线的建设而决定的，它可能会产生不好的充电时间表，也可能对客户的服务订单的决定造成不好的影响，从而导致其性能不佳。

        总的来说，小规模实例的结果表明，BACO是非常有效的。

C.对大规模实例的比较

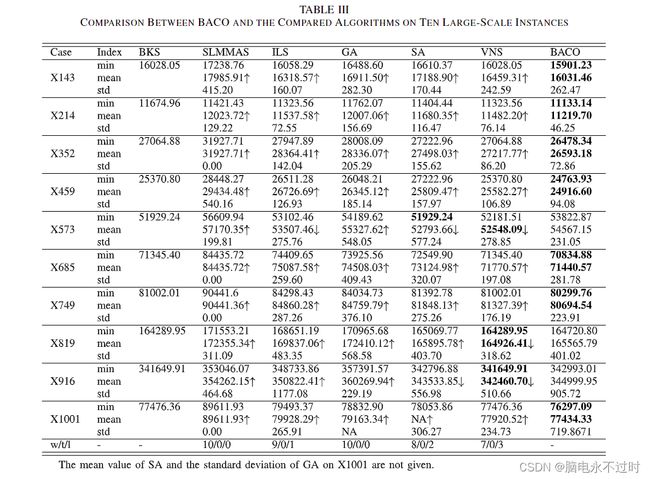
        然后，对大规模实例的算法进行比较。比较结果见表三。从结果中，我们可以得到以下观察。

 1）根据平均目标值和统计学检验，BACO在所有实例上都压倒了SLMMAS和GA。另外，BACO在9个实例上的表现优于ILS，在8个实例上的表现优于SA，在7个实例上的表现优于VNS。根据最小目标值，BACO更新了10个实例中7个实例的最佳已知解，除了X573、X819和X916。这一证据表明，BACO通常是比较算法中最好的一种。

2）在X573、X819和X916上，BACO的表现并不理想。在检查了这些实例的地图后，我们发现这三个实例中的客户是聚集在一起的，而且仓库离客户很远。这种客户分布可能是BACO表现不佳的原因。在补充材料中显示的参数调整实验中，我们发现调整启发式的权重可以提高BACO在这类实例上的性能。我们保留自适应参数调整作为未来的研究方向。

        为了进一步分析BACO的收[行为，用SLMMAS和ILS画出了它的收[曲线，如图6所示。由于其他算法的代码和论文现在还没有公开，所以没有其他算法的趋近曲线。这些数字表明。

1）基本上，BACO在给定的执行时间内，除了最大的一个X1001之外，在大多数实例上都趋于一致。其融合速度比ILS和SLMMAS快。SLMMAS在初始化后甚至没有对某些实例进行处理。这一现象也显示在表三中，SLMMAS在某些实例上的标准偏差值为0.

2 ） BACO 的融合速度的优势源于其在大规模实例上比 ILS 更好的全局搜索能力。ILS每次都会根据一些众所周知的局部搜索和扰动算子，如2-opt和随机双桥，在一个预定的局部区域内生成新的解决方案，这些算子在[22]中使用。在解决大规模实例时，ILS在巨大搜索空间中的全局搜索能力是不够的。与小规模实例相比，在大规模实例上跳出局部最优需要更长的时间。BACO使用一个信息素矩阵来指导解决方案的构建。在优化的早期阶段，当不同连接的信息素值之间的差异不大时，BACO比ILS有更强的全局搜索能力，更能够跳出局部优化。因此，在图6中。，我们可以看到，BACO比ILS有更快的融合速度，最终在给定的时间内得到更好的结果；

3）BACO和SLMMAS在大规模实例上的比较再次证明了BACO的二层优化结构在有效性和效率方面的优势。通过分解决策空间，问题的复杂性被降低，BACO可以专注于有希望的区域，从而导致良好的融合速度。然而，在SLMMAS中，大规模实例的搜索空间是巨大的，这使得它很难找到好的解决方案；

4） 尽管BACO表现出了良好的性能，但就OS-MMAS算法而言，它有两个缺点。第一个是对（13）中参数α和β的敏感性。补充材料中的实验表明，不同的参数设置可能更喜欢不同类型的实例。第二个是执行速度相对较慢。在OS-MMAS中，每个下一个客户都是通过轮盘选择来选择的。如（13）所示，除了加法运算之外，除法运算也经常用于轮盘选择。因此，与其他具有类似时间复杂性但大部分时间使用加法和减法的方法相比，OS-MMAS任务需要更长的时间来生成游览。然而，这两个缺点并不是致命的。从实验结果中可以看出，传统的设置α=1和β=2在大多数情况下都能很好地工作，尽管它可能不是所有情况下的最佳设置。图6表明，就实际执行时间而言，BACO的收敛速度与ILS相比并不慢。

总体而言，表III和图6的结果表明，尽管BACO并没有在每个实例上都优于现有技术的算法，但通常它在大规模实例上既有效又高效。

 D.移除启发式的有效性

        在BACO中，信息素矩阵根据被RH固定的解决方案进行更新。RH的有效性可以极大地影响信息素的更新，从而影响后续的路线构建。为了进一步研究在BACO中使用RH的有效性，我们将其与另外两种简单而有效的启发式方法进行比较。我们不将元启发式算法应用于下层子问题的原因已经在第四节E中解释过了，也就是说，元启发式算法对于解决下层子问题来说太耗时了[56]。

        第一个比较的启发式算法是在[22]和[43]中应用的GH算法。GH算法不断将充电站插入路线中，以导致电力约束的最小违规程度，直到该路线是电力可行的。第二种是前向启发式（FH）。FH算法遵循电动车的轨迹。每当它发现电动车没有足够的电力到达路线上的下一个节点时，它就插入一个充电站。BACO是用这两种启发式算法重新实现的。

1) 使用不同启发式方法比较BACO的性能。

        BACO使用不同的启发式算法对所有实例进行了10次独立运行的测试。由于篇幅所限，图第7节只显示了一些实例上的趋近曲线。完整的结果可以在补充材料中找到。

1）在小规模的实例上，所提出的RH算法要么优于GH和FH，要么具有与GH相当的性能。使用不同的启发式算法几乎对BACO的融合速度没有影响。

2）在大规模实例上，与FH相比，RH在大多数实例上表现出更好的性能，但在其中一些实例上被击败，如X916和X1001。与GH相比，RH总是更好。另外，图中显示，使用RH和FH的BACO的融合速度比使用GH快得多。

        一般来说，我们可以发现RH在小规模基准实例和大规模实例上都是高效的。GH可以在小规模的实例上产生良好的解决方案，但它在处理大规模实例方面并不高效。FH在小规模实例上并不有效，但在大规模实例上可以有效。

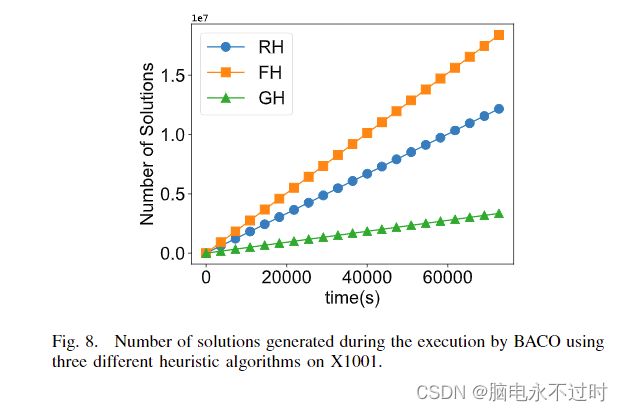
        这种现象可以从时间复杂性的角度来分析。图8显示了在最大实例X1001上执行过程中生成的解决方案数量。从图8中可以看出，这三种算法的时间复杂度排序为GH>RH>FH。最简单的启发式FH算法之所以能在一些大规模实例上获得更好的结果，是因为带有FH的BACO算法比其他两种算法生成了更多的解。在这些大规模的实例中，BACO需要高速才能在有限的执行时间内收敛。因此，使用简单的启发式方法在有限的时间内生成更多的解决方案是一个不错的选择。然而，如果算法能够在有限的执行时间内完全收敛，就像客户少于300的实例上的情况一样，GH和RH可以获得比FH更好的解决方案，因为在这种情况下，生成好的解决方案比生成更多的解决方案更重要。关于本文提出的RH，实验结果表明，它可以在不带来高计算负担的情况下生成非常好的解。

 2）三种启发式算法产生的解决方案的比较。

        为了直观地证明这三种启发式算法的优点和缺点，我们以BACO在E-n23-k3上用这三种启发式算法生成的解决方案为例。解决方案中的充电站首先被移除。然后，通过使用三种启发式算法分别生成三种不同的解决方案，如图9所示。

        1）关于FH，很容易理解，插入充电站的位置可能不是最佳的，因为它只在电动车必须充电的时候给它充电。检查图9(a)中的左边路线。我们可以发现，电动车为两个远离左上角车站的客户提供服务，然后回到车站进行充电。图9(b)和(c)显示，GH和RH在为靠近车站的客户提供服务后，让电动车充电，然后去了两个客户，这与FH不同。

        2）关于GH，如果电动车在旅途中只充电一次，GH总能找到插入充电站的最佳位置。然而，如果电动车在旅途中应该多次充电，它可能无法找到插入充电站的最佳位置，因为GH的目标是最小化违规程度，而不是在路线变得可行之前的目标值。这可能会导致充电站插入的错误位置。从图中的右侧路线来看。9(b)，我们可以看到，它从RH选择的充电站中选择了不同的充电站。

        3）关于RH，在大多数情况下，给定一条具有相同客户订单的路线，它可以产生比GH和FH更好的充电时间表。然而，有一种情况是，RH可能会在一条路线上插入比它真正需要的更多的充电站。假设一种情况，即一条路线可以通过在路线的最中间插入一个充电站或在头部和尾部分别插入两个充电站来固定，在中间插入一个充电站的额外距离比单独插入两个充电站中的每一个都要长，但比一起插入两个充电站要短。在这种情况下，RH会选择第二个计划插入两个比第一个计划差的充电站。

        总的来说，由于FRVCP本质上是一个NP-hard问题[22]，所有这三种启发式算法都不能保证充电时间表的最优性，但从一般性能和案例研究中，我们可以看到，所提出的RH对FH和GH有明显的优势。因此，它是BACO的最佳选择。

E.限制枚举方法的有效性

        为了研究限制枚举方法，比较了BACO在最终细化之前和最终细化之后生成的解。在七个小规模的实例中，我们发现限制枚举方法没有改变解决方案的任何充电时间表。这一结果再次表明，RH足够有效，可以在小规模的情况下产生良好甚至最优的充电时间表。因此，表IV中仅显示了大规模实例的比较。显示了限制枚举方法带来的最佳利润以及BACO的平均性能。给出了限制枚举方法的平均执行时间，表明它不会带来太多额外的计算负担。

        对于前五个实例X143到X573，列举基本上没有什么帮助，只是稍微改善了X352和X573的平均目标值。这一事实意味着RH对少于600个客户的问题已经非常有效。从X685开始，限制性枚举开始显示其有效性。它给BACO在最后五个实例上的性能带来了不同程度的改善。特别是在X685上，它取得了超过百分之一的改进，这对于一个大规模的问题来说是非常大的。此外，检查执行时间，我们可以看到，尽管限制性枚举方法的理论时间复杂度非常高O（n4），但其实际执行时间很短，通常小于th

        总的来说，受限枚举法能有效地提高最终解决方案的质量，并且在不带来太多额外计算成本的情况下足够高效。基于这些结果，我们建议使用限制性枚举法来处理有600多个客户的大规模问题。

IV 结论

        本文的目标是有效地解决CEVRP。这一目标已经通过提出一种叫做BACO的新算法成功实现。具体来说，BACO通过将CEVRP分解为两级子问题CVRP和FRVCP，缩小了CEVRP的搜索空间。然后，将对应于这两个子问题的OS-MMAS和RH协调起来，BACO在解决不同规模的CEVRP方面表现出良好的能力。与最先进的算法的比较表明，BACO在大多数实例上的一般性能明显更好，它甚至更新了七个实例的最佳已知解决方案。进一步的分析也证明了BACO组件的有效性和效率，这也是BACO可以在大规模实例上保持稳定和快速的优化速度的原因。

        尽管BACO在本文中表现出了很好的性能，但仍有许多开放性问题需要研究。首先，实验结果表明，BACO在解决有集群客户的实例方面的能力比解决常规实例要弱。因此，如何在算法中加入方向信息以进一步提高其解决特殊情况的能力是我们未来工作的主要方向。其次，经验和理论分析表明，在解决下层子问题FRVCP时，启发式算法的复杂性和有效性之间存在着权衡。因此，如何在BACO的不同阶段使用不同的启发式算法来充分利用计算资源是提高BACO性能的另一个有希望的方向。