简单ab测试与分析

某打车公司简单分析*
目的：结合学校获得的统计方法，用作AB测试的入门。

数据来源K-lab，此次博客用于记录与探索，分为两个部分；
1.对于整体的运营指标分析，2.初窥AB测试

1.日常导包读入数据

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns 
import datetime
import math
from sklearn.linear_model import LinearRegression
import datetime
matplotlib.rcParams['font.family']='kaiti' 
df=pd.read_excel('C:/Users/韭菜盒子/Desktop/city.xlsx',delimiter=',',encoding='utf-8')
pf=pd.read_excel('C:/Users/韭菜盒子/Desktop/test.xlsx',delimiter=',',encoding='utf-8')  

2.列名更改

df.rename(columns={'date':'日期','hour':'时点','requests':'订单请求数','trips':'订单数','supply hours':'服务时长','average minutes of trips':'平均订单时长','pETA':'顾客预计等待时长','aETA':'顾客实际等待时长','utiliz':'司机在忙率'},inplace=True)
df['接单率']=round(df['订单数']/df['订单请求数'],2)

3.可视化函数
整个可视化都放在一个函数里，看起来比较乱，参考意义不大

def show(data):        
	plt.plot(data.index,data['司机在忙率'].values,'b',label=['司机在忙率'])
        plt.plot(data.index,data['订单率'].values,'r',label=['订单率'])    
        # plt.xticks(rotation=90)
        
    	# plt.show()    
  	# print(df_day_request.sort_values(ascending=False)[:5])    
  	# sns.barplot(data.index,data.iloc[:,2].values,palette='Blues')    
  	for a,b in zip(data.index,data['司机在忙率'].values):        
  		plt.text(a,b,b)    
 	for a,b in zip(data.index,data['订单率'].values):        
 		plt.text(a,b,b)    
 	# plt.xticks(range(len(data.index)),data.index)    
 	# plt.grid()    
 	# plt.pie(data['date_percent'],labels=data.index,shadow=True,autopct='%1.2f%%')
 	plt.legend()
        # plt.title('订单数&&订单请求数')    
        # plt.plot(data.iloc[:,0],data.iloc[:,1],'b.')    
        # plt.plot(data.iloc[:,0],k*data.iloc[:,0]+b,'r')
        plt.show()

4.数据梳理
整体数据比较干净，基本没有什么改动，只是对于个别的字段的异常值进行了检测

# df['日期']=pd.to_datetime(df['日期'])

# print(df)
# print(df[df['顾客预计等待时长']==0])
# print(df[df['顾客实际等待时长']==0])
df['等待时间']=df['顾客实际等待时长']-df['顾客预计等待时长']
#print(df[df['等待时间']<0])

5.运营分析
先讲一下整个分析思路，基本是围绕订单数与请求数展开，争对每个字段进行逐一分析，然后是联合分析，构建一些指标进行观测分析，亮点是结合了我手写的线性回归。（可视化的代码在一个函数里反复调用，细节处反复更改已经面目全非，我就不放具体的了）

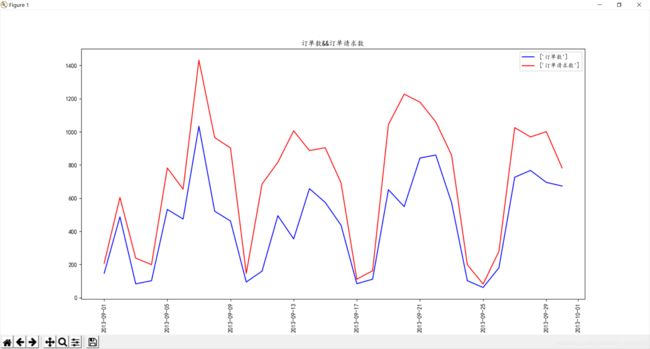
5.1 日期

df_day_respond=df.groupby(by='日期')['订单数'].sum()
df_day_request=df.groupby(by='日期')["订单请求数"].sum()
# show(df_day_respond,df_day_request)

整体趋势呈现周期性变化，就大致来说有5个峰值，4 个谷值，推测这些波峰出现在周末附近，波谷出现在周一。

df['week']=df['日期'].dt.dayofweek
week=['星期一','星期二','星期三','星期四','星期五','星期六','星期天']
# print(df)
d={    '6':'星期天', 
       '0':'星期一',    
       '1':'星期二',    
       '2':'星期三',    
       '3':'星期四',    
       '4':'星期五',    
       '5':'星期六'}df['week']=df['week'].astype(str).replace(d)
df_day_respond=df.groupby(by='日期')['订单数'].sum()
df_day_request=df.groupby(by='日期')["订单请求数"].sum().sort_values(ascending=False)[:5]
# show(df_day_respond,df_day_request)
print(df_day_request)
print(df[((df['日期']=='2013-09-07')|(df['日期']=='2013-09-20')|(df['日期']=='2013-09-21')|(df['日期']=='2013-09-22')|(df['日期']=='2013-09-19'))&(df['时点']==11)])
print(df[((df['日期']=='2013-09-25')|(df['日期']=='2013-09-17')|(df['日期']=='2013-09-10')|(df['日期']=='2013-09-18'))&(df['时点']==11)])

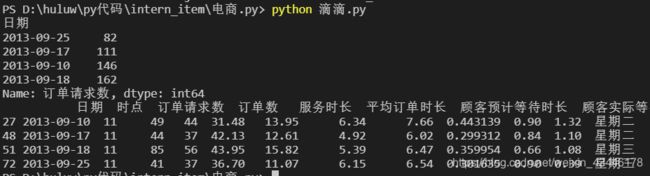
跟推测的还是有一定偏差，峰值主要集中于周末附近，谷值主要集中在周二周三。
考虑在周末添加用车与司机，考虑因素为周末的人们出行，与学生周五放假，对于周二周三可以适当调整车辆与司机的数量，在周二周三让司机轮休调换比较好。

5.2 时点

df_hour=df.pivot_table(index='时点',values=['订单数','订单请求数',],aggfunc={'订单数':'sum','订单请求数':'sum'})
# print(df_hour)
df_hour['date_percent']=df_hour.iloc[:,0]/df_hour.iloc[:,1]

     订单数  订单请求数  date_percent

时点
11 4550 6008 0.757324
12 5850 8530 0.685815
13 3085 6559 0.470346

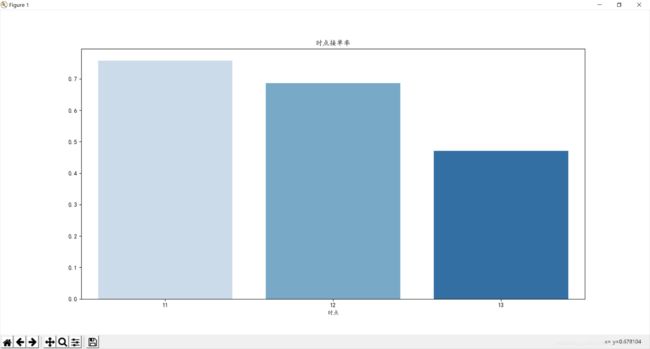
可以看出11点订单的完成率最高，依次下降13点最低，只有47%的完成率
（在这里要注意一个问题，之前添加了一个字段接单率，正常来说，直接按时间分组，然后求接单率的平均值，这样看上去没有问题，可是每天的每一个时点都求了它的接单率这本身是有一定误差的，要考虑不能整除的因素，那为了简洁明了又采取round函数，这样累计下来的结果是十分不精确的）

5.3 服务时长&&平均订单时长

服务时长分布如图。

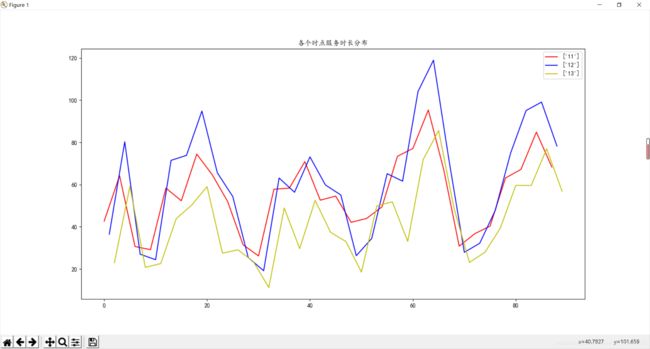
对于平均订单时长着重探索于13点分布，可以看出订单的时长可能不是影响13点订单完成率的主要因素，可进行别的方法和数据去探究影响因素

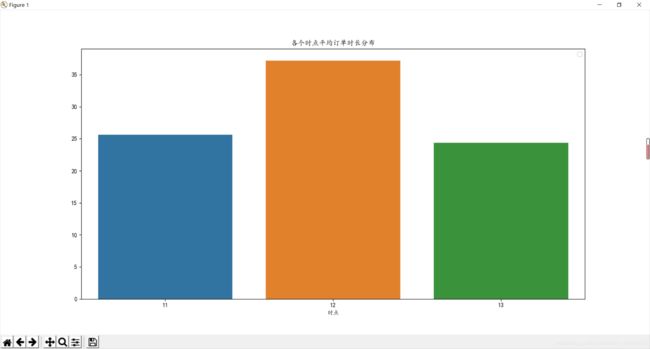
5.4顾客预计等待时长&&顾客实际等待时长&&等待时间

df_hour_wait=df.pivot_table(index='时点',values=['顾客预计等待时长','顾客实际等待时长','等待时间'],aggfunc={'顾客预计等待时长':'mean','顾客实际等待时长':'mean','等待时间':'mean'})
print(df_hour_wait)
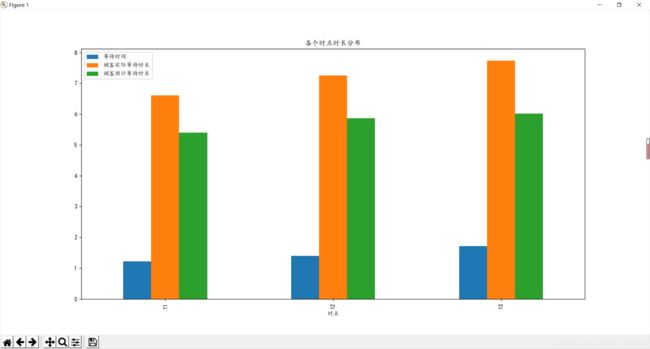
# df_hour_wait.plot(kind='bar')
# plt.title('各个时点时长分布')
# plt.show()

    等待时间  顾客实际等待时长  顾客预计等待时长

时点
11 1.213667 6.611000 5.397333
12 1.393333 7.253333 5.860000
13 1.714333 7.732667 6.018333

时间部分联合展示，按时点分组后，对于每一个字段取了均值，可以看到，11点的等待时间是比较短，13点最长，根据之前提供的信息，13点的订单完成率也是比较低的，这两个因素是相互影响的。

5.5 在忙率
在忙率根据时点分组取平均

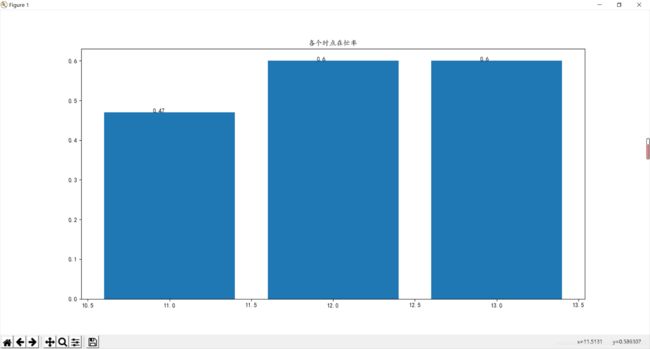
由图可知，12，13点的在忙率近乎相同，在这里取了round（data,2），可能看上去一样
根据之前得到的信息，12点的订单完成率为0.68，13点则为0.47，13点的平均订单时长是最低的，
由此说明，13点，平均订单所占用的时间是比较少的，常规思维，订单时长的减少，本应该有更多的空闲车辆，而其订单的完成率却为47%，在忙率高达60%，这显然是不正常的，这说明，在原有的订单基础上，车辆已经难以应付订单请求，要着重考虑13点时的车辆分布，和地区原因还有车辆的数量，以及其他隐形问题是否存在。
接下来是对于在忙率一个简单的探索。
先看了一下相关系数

print(df.head(3))
mf=df.copy()
mf.drop('日期',axis=1,inplace=True)
for column in mf:    
	data=df[[column,'司机在忙率']]
        a=pd.Series(data.iloc[:,0].values)    
        b=pd.Series(data.iloc[:,1].values)    
        corr_gust = round(a.corr(b), 4)    
        print(column,corr_gust)

时点 0.3341
订单请求数 0.414
订单数 0.1981
服务时长 -0.1189
平均订单时长 0.4125
顾客预计等待时长 0.5604
顾客实际等待时长 0.6659
司机在忙率 1.0
接单率 -0.3977
等待时间 0.2205

可以看出相关关系的密切程度最高的是顾客实际等待时长，且因为数据取自9.1-9.30 是整体数据 ，即不用做关于相关系数的显著性的检验
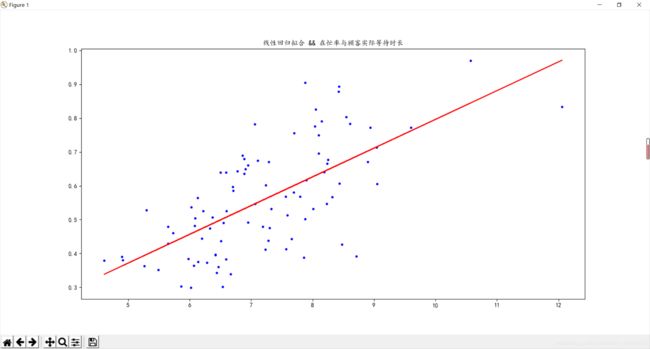
至此，开始探索顾客实际等待时长与在忙率的关系
highlight： 惊喜的是，这次手写的线性回归跟sklearn模拟的高度重合
附上代码；

epochs=10000
k=0
b=0
lr=0.0001
def loss_function(x_data,k,b,lr,epochs):    
	m=float(len(x_data))    
	loss=0    
	for i in range(len(x_data)):        
	loss+= ((k*x_data.iloc[i,0]+b)-x_data.iloc[i,1])**2 /(2*m)    
	# print(loss)    
	# print(data)
# loss_function(data,k,b,lr,epochs)
# print(x_data)
def gradient_decent(x_data,k,b,lr,epochs):    
	for j in range(epochs):        
		k_brad=0        
		b_brad=0        
		for i in range(len(x_data)):            
			k_brad+=((k*x_data.iloc[i,0]+b)-x_data.iloc[i,1])*x_data.iloc[i,0]            
			b_brad+=((k*x_data.iloc[i,0]+b)-x_data.iloc[i,1])        
		k=k-lr*k_brad        
		b=b-lr*b_brad    
	# print(k,b)    
	return k,b
k,b=gradient_decent(data,k,b,lr,epochs)
# show(k,b,data)
print(k,b)
#sklearn
model=LinearRegression()
data=pd.DataFrame(data)
x_data=data.iloc[:,0].values
x_data=pd.DataFrame(x_data)
y_data=data.iloc[:,1].values
y_data=pd.DataFrame(y_data)
model.fit(x_data,y_data)
print(model.intercept_)
print(model.coef_)
def linear_model_show():    
	plt.plot(data.iloc[:,0],data.iloc[:,1],'y.')
	plt.plot(data.iloc[:,0],k*data.iloc[:,0]+b,'b')
	
    	plt.plot(x_data,model.predict(x_data),'r')    
    	plt.show()

#me
0.08495177707829321 -0.05328230595522736
假装是分割线---------
#sklearn
[-0.0588547]
[[0.08570417]]

拟合情况还是比较好，但是代码的运行速度令人堪忧，这里没有放出来运行的时间，，还是没有sklearn方便。
y=0.085x-0.05
如图所示
在忙率可能更应该关注顾客实际等待时长
至此，基本分析完毕，进入AB测试

6.AB测试
6.1说明
指标说明

def AB_text(pf):    
print(pf.head())    
pf.rename(columns={'date':'时点','group':'组别','requests':'订单请求数','gmv':'gmv',    'coupon per trip':'优惠卷金额','trips':'订单数','canceled requests':'取消请求数'},inplace=True)    
#电商ROI    
pf['ROI']=pf['gmv']/(pf['优惠卷金额']*pf['订单数'])

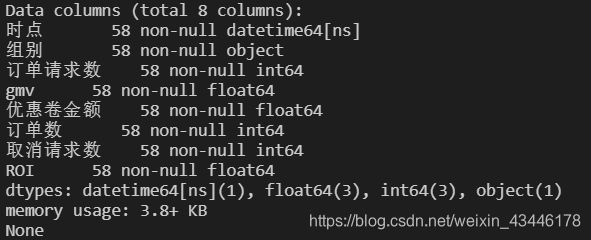
6.2
基本数据如上图所示：分为控制组（control）:A 和实验组（experiment） :B 样本数量=29。整个测试分为手动计算和sta检验。
先大致讲一下AB测试的选择样本：
ab测试流程该是：通过整个用户旅程进而获得整个过程的转化率，找到转化率瓶颈进行改善，故此，ab测试的意义在于对于转化率较低的某个行为进行测试寻求目前的较好的方案
1.进行分流，取得可以代表总体的两组样本，样本可以来自分层抽样，通过各方渠道我们可以获得用户画像比例，再分别抽取相应比例的人数，要注意的是同层互斥，即同一行记录不能出现在两个样本里面，且在测试的时候呢，最好是在同一时间里抽取样本。
#还可以进行AA测试，即在原方案的情况下进行空跑，看看指标是否有显著性的差异，如果没有说明这两个样本拥有一样的用户特性。
2.现在我们得到了两组样本，开始AB测试，周期7-14天或者更长一点，
回到数据集，这个test 表来源kaggle是进行了ab测试后的数据，我们把它当成两组独立样本，开始对ab测试的结果进行一个分析。
具体对于3个指标进行结果的检验分析：订单转化率，GMV,ROI
6.2.1
订单转化率：
1.分别求了订单转化率的均值和方差

import scipy.stats as st
pf_A_request=pf[pf['组别']=='control']
pf_B_request=pf[pf['组别']!='control']
pf_A_request_mean=pf_A_request['订单数'].sum()/pf_A_request['订单请求数'].sum()
pf_B_request_mean=pf_B_request['订单数'].sum()/pf_B_request['订单请求数'].sum()

pf_A_request_data=round(pf_A_request['订单数']/pf_A_request['订单请求数'],3)
pf_B_request_data=round(pf_B_request['订单数']/pf_B_request['订单请求数'],3)

 print(pf_A_request_mean)
 print(pf_B_request_mean)
 

A: 0.7975205221369936
B: 0.7991322404740601
实验组订单转化率均值>控制组均值
结果：控制组均值小于实验组，我们检验是否真的实验组均值大于控制组
假设检验：H0: pf_b_request<=pf_a_request; H1: pf_b_request>pf_a_request 右尾检验
手动计算：

SW=np.sqrt((28*pf_A_request_data.var() + 28*pf_B_request_data.var())/56 )
 t=(pf_B_request_mean-pf_A_request_mean)/(SW*np.sqrt(1/29 +1/29))

结果为：0.5534844214307618 sta计算：

pf_request_result,result=st.ttest_ind_from_stats(mean1=pf_B_request_mean,std1=pf_B_request_data.std(), nobs1=29, mean2=pf_A_request_mean, std2=pf_A_request_data.std(), nobs2=29)
print(pf_request_result)
print(result/2)

用st.ttest_ind_from_stats而不是rel 是因为此次的数据为双总体独立样本而不是相关样本
Ttest_indResult(statistic=0.5534844214307617, pvalue=0.5821349396578142)
右尾检验p-value/2
计算与检验结果相同
且p-value/2>0.025 接受原假设。这个p的含义是假定原假设为真，小概率事件不会发生的思想下出现这个样本的概率是多少，然后用得到的p值与显著性水平衡量（一般取0.05）进行比较，如果>0.05就说取的这个样本概率大于显著性水平，则原假设为真，不显著，反之认为原假设不成立，显著。
2.置信区间：

 t_ci=st.t.ppf(1-0.025,56)
    #t查表自由度为56的0.025
    print(t_ci)
    #标注误差
    se=np.sqrt(pf_A_request_data.var()/29 + pf_B_request_data.var()/29 )
    sample_top_limit=pf_B_request_mean-pf_A_request_mean +(t_ci*se)
    sample_low_limit=pf_B_request_mean-pf_A_request_mean -(t_ci*se)
    print('置信区间',sample_low_limit,sample_top_limit)
    CI=st.t.interval(0.975,56,pf_B_request_mean-pf_A_request_mean,se)
    print(CI)

2.0032407174966975
置信区间 -0.0042216162120820465 0.0074450528862148755
(-0.005095289099392335, 0.00831872577352517)
置信区间说明：
上下限都为正或都为负，说明存在显著差异
一正一负则说明不显著
6.2.2GMV

pf_A_gmv=pf[pf['组别']=='control']['gmv']
pf_B_gmv=pf[pf['组别']=='experiment']['gmv']
#pf_A_gmv_var=pf_A_gmv.var()
#pf_B_gmv_var=pf_B_gmv.var()

# print(pf_a_b_gmv_var)



pf_A_gmv_mean=pf_A_gmv.mean()
pf_B_gmv_mean=pf_B_gmv.mean()

A: 485123.5972413793
B: 479012.4313793103
这里我们看到，控制组的GMV均值是大于实验组的GMV
假设检验：h0:pf_A_gmv_mean<=pf_B_gmv_mean h1:pf_A_gmv_mean>=pf_B_gmv_mean 右尾

SW=np.sqrt((28*pf_A_gmv_var + 28*pf_B_gmv_var)/56)
    t_result=(pf_A_gmv_mean-pf_B_gmv_mean)/(SW*np.sqrt(1/29 + 1/29))
    # print(t_result)
    #0.07728616692818668
    t_result=st.ttest_ind_from_stats(mean1=pf_A_gmv_mean,std1=pf_A_gmv.std(),nobs1=29, mean2=pf_B_gmv_mean,std2=pf_B_gmv.std(),nobs2=29)
    # print(t_result)

0.0772861669281867 Ttest_indResult(statistic=0.07728616692818668, pvalue=0.9386713733961323)
可以看到计算与t统计量的结果是相同的的，在sta里面呢，p-value=0.46933568669806613>0.05 也是接受原假设
置信区间

se=np.sqrt(1/29 +1/29)
    sample_top_limit=pf_A_gmv_mean-pf_B_gmv_mean + (t_ci*se*SW)
    sample_low_limit=pf_A_gmv_mean-pf_B_gmv_mean - (t_ci*se*SW)
    print('置信区间',sample_low_limit,sample_top_limit)
    CI=st.t.interval(0.975,56,pf_A_gmv_mean-pf_B_gmv_mean,se*SW)
    print(CI)

置信区间 -152288.9304662644 164511.2621904024
(-176012.90315176806, 188235.2348759062)

6.2.3ROI

pf_A_roi=pf[pf['组别']=='control']['ROI']
pf_B_roi=pf[pf['组别']!='control']['ROI']
#pf_A_roi_var=pf_A_roi.var()
##pf_B_roi_var=pf_B_roi.var()
pf_A_roi_mean=pf_A_roi.mean()
pf_B_roi_mean=pf_B_roi.mean()
# print(pf_A_roi_mean,pf_B_roi_mean)

控制组: 360.3673233425277
实验组: 351.6809064747571
可以得到控制组ROI均值>实验组ROI均值
假设检验：h0:pf_A_roi_mean<=pf_B_roi_mean h2;pf_A_roi_mean>pf_B_roi_mean 右尾检验

SW=np.sqrt((28*pf_A_roi_var + 28*pf_B_roi_var)/56)
t_result=(pf_A_roi_mean-pf_B_roi_mean)/(SW*np.sqrt(1/29 + 1/29))
# print(t_result)
pf_request_result,result=st.ttest_ind_from_stats(mean1=pf_A_roi_mean,std1=pf_A_roi.std(),nobs1=29, mean2=pf_B_roi_mean,std2=pf_B_roi.std(),nobs2=29)
# print(pf_request_result,result/2)

手动计算：0.8430996450057455
Sta: Ttest_indResult(statistic=0.8430996450057455, pvalue=0.40275951535453325/2)
可以得到计算与检验的结果相同
0.84309964500574550.025 则说明接受原假设，结果不显著。
置信区间

#置信区间：
se=np.sqrt(pf_A_roi_var/29 +pf_B_roi_var/29)
sample_top_limit=pf_A_roi_mean-pf_B_roi_mean + t_ci*se
sample_low_limit=pf_A_roi_mean-pf_B_roi_mean - t_ci*se
# print('置信区间',sample_low_limit,sample_top_limit)
CI=st.t.interval(0.975,56,pf_A_roi_mean-pf_B_roi_mean,se)
# print(CI)

置信区间 -11.952880114200767 29.325713849742
(-15.044078473280951, 32.416912208822204)
小结：
分别对3项指标进行了检验分析，经过检验后发现这三项指标是没有显著性的差异，仅仅对于此次数据来说设定的显著性水平而言，如果设定为1%，可能结果会产生变化，这个显著性水平取决于该平台原方案的实际情况，如果是原本的方案比较好，转化率较高，那么精益求精，将显著性水平设的高一点，也是可以的，反之，就设定的宽松一些。对于拿到的数据而言来说，此次的控制组和实验组没有显著性的差异，实验方案相比于原方案没有明显的显著性差异仅对于这三个指标而言，建议重新设计新的方案进行AB测试。
总结：
1.一开始就使用T检验是因为首先样本数小于30，且近似服从正态分布，所以采用T检验。
2.没有进行方差齐性的检验是因为这本身就是来自一个总体，不需要进行检验，此次分析的前提是基于一个打车公司的an测试，当时分流，抽样时肯定是从同一个整体里抽样，即同层互斥的原理。网上有很多人在那进行方差齐性的检验，没必要。
3.不要瞎套公式，用python的scipy.sta时，在此次检验是T检验，采用的是双独立样本检验，不是相关样本检验；前者用的是ind;后者用的是rel.