leetcode 636. Exclusive Time of Functions

Given the running logs of n functions that are executed in a nonpreemptive(非抢占式) single threaded CPU, find the exclusive time of these functions.

Each function has a unique id, start from 0 to n-1. A function may be called recursively or by another function.

A log is a string has this format : function_id:start_or_end:timestamp. For example, "0:start:0" means function 0 starts from the very beginning of time 0. "0:end:0" means function 0 ends to the very end of time 0.

Exclusive time of a function is defined as the time spent within this function, the time spent by calling other functions should not be considered as this function's exclusive time. You should return the exclusive time of each function sorted by their function id.

Example 1:

Input:
n = 2
logs = 
["0:start:0",
 "1:start:2",
 "1:end:5",
 "0:end:6"]
Output:[3, 4]
Explanation:
Function 0 starts at time 0, then it executes 2 units of time and reaches the end of time 1. 
Now function 0 calls function 1, function 1 starts at time 2, executes 4 units of time and end at time 5.
Function 0 is running again at time 6, and also end at the time 6, thus executes 1 unit of time. 
So function 0 totally execute 2 + 1 = 3 units of time, and function 1 totally execute 4 units of time.

Note:

1. Input logs will be sorted by timestamp, NOT log id.
2. Your output should be sorted by function id, which means the 0th element of your output corresponds to the exclusive time of function 0.
3. Two functions won't start or end at the same time.
4. Functions could be called recursively, and will always end.
5. 1 <= n <= 100

这道题题目说的云里雾里的，还说什么非抢占式CPU。我后来弄明白了，非抢占式跟题目一点关系都没有，抢占是一个线程抢占另一个线程，但是题目中只有function，而一个方法调用另一个方法不算抢占。这道题的意思是，后开始的方法一定先结束。就像括号一样，左括号代表开始，右括号代表结束，可以是 {{{}}}，也可以是 {{}{}} 。

还有大神问：

0----1----2----3----4----5----6

fun0 ：占用了 0~1, 1~2 。 一共占用 2 时间单元
fun1 ：占用了 2~3, 3~4, 4~5 。一共占用了 3 时间单元。
fun0 ：占用了 5~6 。一共占用了1 时间单元。

为什么func1 最后结果是占用了 4 时间单元呢？

有人回答：

不要把 x 看做一个不占时间的时刻，而应当看做是一个占时间的时间项目(时间单元)。

[0][1][2][3][4][5][6]

fun0 ：占用了前 2 个 boxes
fun1 ：占用了接下来4个 boxes
fun0 ：占用了最后1个 box

看看这几个测试用例：

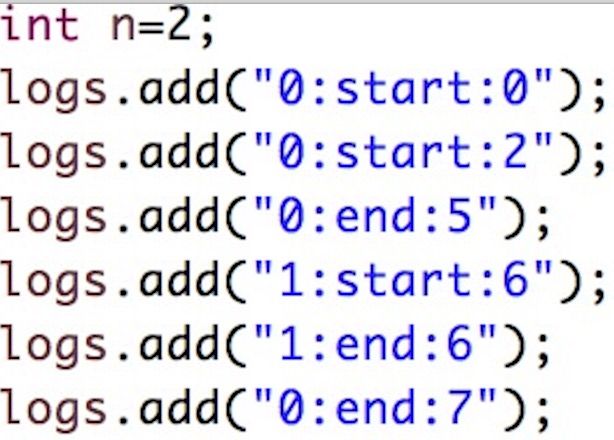
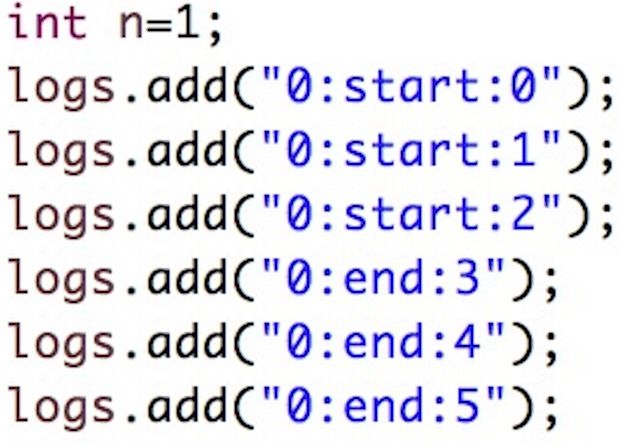
1. 

2.

既然是后开始的方法先结束，那我当然就想到了用栈来做。

public int[] exclusiveTime(int n, List logs) {
	int[] time=new int[n];
	//stack存:所有的start
	//int[0]存:functionId,int[1]存:timePoint,int[2]存:被别人占用的时间
	Stack stack=new Stack();
	for(String s:logs){
		String[] it=s.split(":");
		int id=Integer.parseInt(it[0]);
		String startOrEnd=it[1];
		int timePoint=Integer.parseInt(it[2]);
		if(startOrEnd.equals("start")){
			stack.push(new int[]{id,timePoint,0});
		}
		else{//startOrEnd.equals("end")
			int[] the=stack.pop();
			int usedTime=timePoint+1-the[1]-the[2];
			time[id]+=usedTime;
			//对于当前还在栈中的每个function
			//都被当前function占用了时间
			ArrayList list=new ArrayList();
			while(!stack.isEmpty()){
				int[] tmp=stack.pop();
				tmp[2]+=usedTime;				
				list.add(tmp);
			}
			for(int i=list.size()-1;i>=0;i--){
				stack.push(list.get(i));
			}
		}
	}
	return time;
}

这道题有solutions： https://leetcode.com/problems/exclusive-time-of-functions/solution/

Approach #2 Better Approach [Accepted]

Algorithm

首先要弄明白一点：当遍历到logs中的某个字符串时，无论它是begin还是end，当前位于栈顶的元素都会占用 “当前字符串的timePoint-之前字符串的timePoint”(或+1) 时间。

因为如果当前遍历到的字符串是start，那么栈顶元素就是之前start了还没结束的function，在 当前时间点 和 上一个时间点 之间的这段时间，是被栈顶元素占用的，占用了 “当前字符串的timePoint-之前字符串的timePoint” 时间。

如果当前遍历到的字符串是end，那么栈顶元素就是 当前字符串的function (前面一个字符串刚push进了该function的start) ，那么在 当前时间点 和 上一个时间点 之间的这段时间，也肯定是被栈顶元素占用的，占用 “当前字符串的timePoint-之前字符串的timePoint +1 ” 时间 (比之前多加了一个end时间点)。   

举个例子来说明：

functionId:   0  1  2   2   1    0
begin/end:   {   {   {    }    }    }
timeItem:     0  1  2   3   4    5

0 被push进栈后，接下来遍历到 1 start 1，那么 0~1 的时间是被栈顶元素 0 占用的。接下来 1 被push进栈，遍历到 2 start 2，那么 1~2 的时间是被栈顶元素 1 占用的。接下来 2 被push进栈，遍历到 2 end 3，那么 2~3 的时间是被栈顶元素 2 占用的。接下来pop出 2 ，遍历到 1 end 4，那么3~4的时间是栈顶元素 1 占用的。接下来pop出 1 ，遍历到 0 end 5，那么 4~5 的时间是栈顶元素 0 占用的。

所以算法的关键在于：拿到上一个log的 start/stop time 设为prev，再拿到当前 log 的 start/stop time ，计算出两个time之间的时间差。

Java

public class Solution {
    public int[] exclusiveTime(int n, List < String > logs) {
        Stack < Integer > stack = new Stack < > ();
        int[] res = new int[n];
        String[] s = logs.get(0).split(":");
        stack.push(Integer.parseInt(s[0]));
        int i = 1, prev = Integer.parseInt(s[2]);
        while (i < logs.size()) {
            s = logs.get(i).split(":");
            if (s[1].equals("start")) {
                if (!stack.isEmpty())
                    res[stack.peek()] += Integer.parseInt(s[2]) - prev;//起点算，终点不算
                stack.push(Integer.parseInt(s[0]));
                prev = Integer.parseInt(s[2]);
            } else {
                res[stack.peek()] += Integer.parseInt(s[2]) - prev + 1;//起点算，终点也算
                stack.pop();
                prev = Integer.parseInt(s[2]) + 1;//s[2]已经算作了该function的终点，不能再作为起点(起点肯定算)
            }
            i++;
        }
        return res;
    }
}

Complexity Analysis

• Time complexity : $O(n)$. We iterate over the entire $logs$ array just once. Here, $n$ refers to the number of elements in the $logs$ list.

• Space complexity : The $stack$ can grow upto a depth of atmost $n/2$. Here, $n$ refers to the number of elements in the given $logs$ list.