相似性搜索:第 3 部分--混合倒排文件索引和产品量化
接续前文:相似性搜索:第 2 部分:产品量化
SImilarity 搜索是一个问题,给定一个查询的目标是在所有数据库文档中找到与其最相似的文档。
一、介绍
在数据科学中,相似性搜索经常出现在NLP领域,搜索引擎或推荐系统中,其中需要检索最相关的文档或项目以进行查询。在大量数据中,有各种不同的方法可以提高搜索性能。
在本系列的前两部分中,我们讨论了信息检索中的两种基本算法:倒排文件索引和产品量化。它们都优化了搜索性能,但专注于不同的方面:前者加快了搜索速度,而后者将向量压缩为更小、节省内存的表示形式。
由于两种算法都关注不同的方面,因此自然出现的问题是是否可以将这两种算法合并为一种新的算法。
在本文中,我们将结合这两种方法的优点来生成一种快速且内存高效的算法。作为参考,大多数讨论的想法将基于本文。
在深入研究细节之前,有必要了解残差向量是什么,并对它们的有用特性有一个简单的直觉。稍后我们将在设计算法时使用它们。
三、残差向量
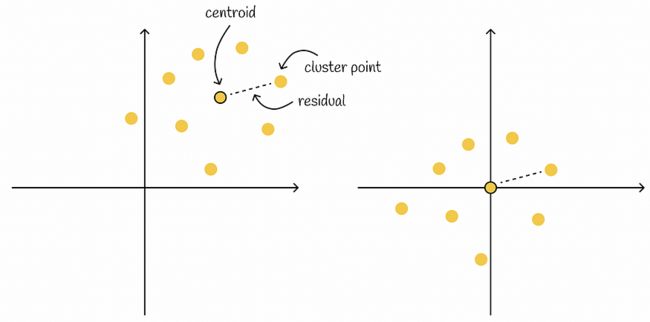
假设执行了一个聚类算法,它产生了几个聚类。每个聚类都有一个质心和与之关联的点。残差是点(向量)与其质心的偏移量。基本上,要找到特定向量的残差,必须从其质心中减去该向量。
如果聚类是通过 k 均值算法构建的,则聚类质心是属于该聚类的所有点的平均值。因此,从任何点找到残差等效于从中减去聚类的平均值。通过从属于特定聚类的所有点中减去平均值,这些点将以 0 为中心。
左侧显示了原始点聚类。然后从所有聚类点中减去聚类质心。生成的残差向量显示在右侧。
我们可以观察到一个有用的事实:
用残差替换原始向量不会改变它们之间的相对位置。
也就是说,向量之间的距离始终保持不变。让我们简单地看下面的两个等式。
减去平均值不会改变相对距离
第一个方程是一对向量之间的欧几里得距离公式。在第二个方程中,从两个向量中减去聚类平均值。我们可以看到平均项只是抵消了 — 整个表达式与第一个方程中的欧几里得距离相同!
我们使用 L2 度量(欧几里得距离)的公式证明了这一说法。请务必记住,此规则可能不适用于其他指标。
因此,如果对于给定查询的目标是查找最近的邻居,则可以仅从查询中减去聚类均值,然后继续执行残差中的正常搜索过程。
从查询中减去平均值不会改变其与其他向量的相对位置
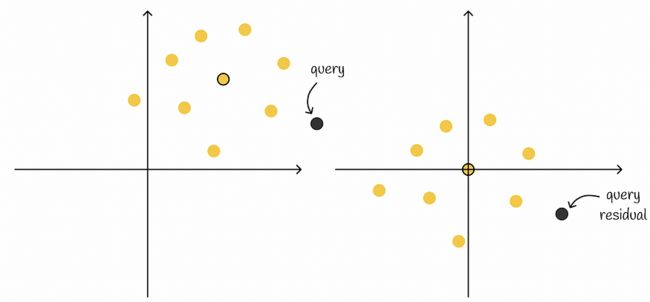
现在让我们看下图中的另一个示例,其中包含两个聚类,其中每个聚类的向量的残差分别计算。
从聚类的每个向量中减去相应质心的平均值将使所有数据集向量以 0 为中心。
这是一个有益的意见,今后将加以利用。此外,对于给定的查询,我们可以计算所有聚类的查询残差。查询残差允许我们计算到聚类原始残差的距离。
从每个聚类中减去平均值后,所有点都以 0 为中心。从查询和查询残差到相应聚类的其他点的相对位置不会更改。
四、训练
在考虑了上一节中有用的观察结果后,我们可以开始设计算法了。
给定一个向量数据库,构造一个倒排文件索引,将向量集划分为 n 个 Voronoi 分区,从而在推理过程中缩小搜索范围。
在每个 Voronoi 分区内,从每个向量中减去质心的坐标。结果,来自所有分区的向量彼此更靠近并以 0 为中心。此时,不需要原始向量,因为我们存储它们的残差。
之后,乘积量化算法在所有分区的向量上运行。
重要方面:产品量化不会为每个分区单独执行 - 这将是低效的,因为分区的数量通常往往很高,这可能会导致存储所有码本所需的大量内存。相反,该算法将同时对所有分区中的所有残差执行。
实际上,现在每个子空间都包含来自不同Voronoi分区的子向量。然后,对于每个子空间,执行聚类算法,并像往常一样构建 k 个聚类及其质心。
训练过程
用残差替换载体的重要性是什么?如果向量没有被它们的残差替换,那么每个子空间将包含更多不同的子向量(因为子空间将存储来自不同非相交Voronoi分区的子向量,这些子向量在空间中可能彼此相距很远)。现在,来自不同分区的向量(残差)彼此重叠。由于现在每个子空间的种类较少,因此需要更少的复制值来有效表示向量。换句话说:
使用与之前使用的 PQ 代码长度相同的代码,矢量可以更准确地表示,因为它们具有较小的方差。
五、推理
对于给定的查询,可以找到 Voronoi 分区的 k 个最近的质心。这些区域内的所有点都被视为候选点。由于原始向量最初被每个 Voronoi 区域中的残差替换,因此还需要计算查询向量的残差。在这种情况下,需要为每个 Voronoi 分区单独计算查询残差(因为每个区域都有不同的质心)。只有来自所选 Voronoi 分区的残差才会归候选人所有。
然后将查询残差拆分为子向量。与原始乘积量化算法一样,对于每个子空间,计算包含从子空间质心到查询子向量的距离的距离矩阵 d。必须记住,每个Voronoi分区的查询残差是不同的。基本上,这意味着需要为每个查询残差单独计算距离矩阵 d。这是所需优化的计算价格。
最后,对部分距离进行总结,就像之前在乘积量化算法中所做的那样。
5.1 排序结果
计算完所有距离后,需要选择 k 个最近邻。为了有效地做到这一点,作者建议维护一个MaxHeap数据结构。它的容量有限,为k ,每一步,它存储k电流最小距离。每当计算新距离时,仅当计算的值小于 MaxHeap 中的最大值时,才会将其值添加到 MaxHeap 中。计算完所有距离后,查询的答案已经存储在 MaxHeap 中。使用MaxHeap的优点是其快速的构建时间,即O(n)。
推理过程
六、性能
该算法利用倒排文件索引和乘积量化。根据推理期间 Voronoi 分区探测的数量,需要计算相同数量的子向量到质心矩阵 d 并将其存储在内存中。这可能看起来像是一个缺点,但将其与整体优势相比,这是一个相当不错的权衡。
该算法从倒排文件索引继承了良好的搜索速度,从产品量化中继承了压缩效率
七、费斯实施
Faiss(Facebook AI Search Similarity)是一个用C++编写的Python库,用于优化的相似性搜索。该库提供了不同类型的索引,这些索引是用于有效存储数据和执行查询的数据结构。
根据 Faiss 文档中的信息,我们将了解如何将倒置文件和产品量化索引组合在一起以形成新的索引。
Faiss 在 IndexIVFPQ 类中实现了所描述的算法,该类接受以下参数:
- 量化器:指定如何计算向量之间的距离。
- D:数据维度。
- nlist:Voronoi 分区的数量。
- M:子空间的数量。
- nbits:对单个集群 ID 进行编码所需的位数。这意味着单个子空间中的总聚类数将等于 k = 2^nbits。
此外,还可以调整 nprobe 属性,该属性指定在推理过程中必须使用多少个 Voronoi 分区来搜索候选者。更改此参数不需要重新训练。
费斯对IndexIVFPQ的实现
存储单个向量所需的内存与原始产品量化方法相同,只是现在我们再添加 8 个字节以在倒排文件索引中存储有关向量的信息。
八、结论
利用上一篇文章部分中的知识,我们演练了实现高内存压缩和加速搜索速度的最先进算法的实现。该算法在处理大量数据时广泛用于信息检索系统。
资源
- 最近搜索的产品量化
- 费斯文档
- 费斯存储库
- 费斯指数摘要
除非另有说明,否则所有图片均由作者提供。