《算法系列》之回溯
简介
回溯算法是一种深度优先搜索算法，所以深搜的特点回溯算法都有。比如：一、它是一种递归算法。二、它是一种暴力算法。三、本质是穷举，穷举所有可能，然后找出我们想要的答案。其实如果你面试的时候遇到回溯算法的题，你应该要笑醒了。因为这是一种有“模板”的题，一通百通的哪种。而不会像动态规化哪样的题，没有固定套路，做不做的出来全看命。回溯题一般也是中等难度，很适合面试考，一两天时间就可以吃透，可以说性价比很高了，我们要做的只是记住模板而已！有时一道题可用动规法去做，也可用回溯法去做，这时我们应该考虑优先用动规法去做，因为回溯的效率还是太低了。
理论基础
回溯算法是对树形或者图形结构执行一次深度优先遍历，实际上类似枚举的搜索尝试过程，在遍历的过程中寻找问题的解。深度优先遍历有个特点：当发现已不满足求解条件时，就返回，尝试别的路径。此时对象类型变量就需要重置成为和之前一样，称为状态重置。许多复杂的，规模较大的问题都可以使用回溯法，有通用解题方法的美称。实际上，回溯算法就是暴力搜索算法，它是早期的人工智能里使用的算法，借助计算机强大的计算能力帮助我们找到问题的解。一般情况下，组合问题、切割问题、子集问题、排列问题、棋盘问题可考虑使用回溯解题，这些的题的特点都是：都可以抽象为树形结构。
回溯的模板
接下来是最重要的模板部分，回溯的模板，其实就是从深搜的递归中演变而来。需要注意以下几点：
- 回溯算法中函数返回值一般为void，但一般需要一个结果集用于存结果。
- 回溯算法的参数一般不固定，需要什么传什么就可以了。
- 既然是递归算法，就需要注意终止条件，一般为题目要求。
- 回溯算法的核心之一在于：状态重置，即回到操作之前的状态。
伪代码实现
void backtracking(路径，选择列表，结果集...) {
if (终止条件) {
存放结果操作;
return;
}
for (i = start; i <= n && (剪枝操作); i++) { // 剪枝操作不强制要求有
处理当前节点;
backtracking(路径，选择列表，结果集...); // 递归
状态重置，撤销处理结果
}
}
解题心得
- 解回溯题记住回溯模板是第一奥义。
- 回溯算法是一种深度优先遍历算法，也是一种暴力搜索算法，更是一种递归算法。
- 既然回溯题是一种深度优先搜索，那么常见的优化方式，其实就是剪枝与记忆化搜索。
- 回溯算法因为是暴力穷举，所以效率上并不是很高，不到万不得已不要选择。
- 单纯求结果数时，一般用DP，但需要求过程时，则一定会用回溯，这也是一种类型题，要注意。
- 一般情况下，组合问题、切割问题、子集问题、排列问题、棋盘问题可考虑使用回溯解题。
- 回溯法能解决的问题，一定是可以抽象为树形结构的。
- 上节回溯模板中的注意事项要切记。
算法题目
17. 电话号码的字母组合
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
public List letterCombinations(String digits) {
// 结果集
List res = new ArrayList<>();
// 若为空，直接返回
if (digits == null || digits.length() == 0) {
return res;
}
// 拼接字符串用StringBuilder
StringBuilder temp = new StringBuilder();
String[] numString = new String[]{"0", "1", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
// 迭代递归
backTracking(digits, temp, numString, 0, res);
return res;
}
public void backTracking(String digits, StringBuilder temp, String[] numString, int num, List res) {
// 递归出口
if (num == digits.length()) {
res.add(temp.toString());
return;
}
String str = numString[digits.charAt(num) - '0'];
for (int i = 0; i < str.length(); i++) {
temp.append(str.charAt(i));
backTracking(digits, temp, numString, num + 1, res);
// 去掉最后一位，继续尝试
temp.deleteCharAt(temp.length() - 1);
}
}
}
22. 括号生成
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
public List generateParenthesis(int n) {
List res = new ArrayList<>();
generate(res, 0, 0, "", n);
return res;
}
public void generate(List res, int l, int r, String tmp, int n) {
// 当字符串长度为 n*2 时，到达递归出口
if (tmp.length() == n * 2) {
res.add(tmp);
return;
}
// 左括号数不能大于总括号数
if (l < n) {
generate(res, l + 1, r, tmp + "(", n);
}
// 右括号不能大于左括号数
if (r < l) {
generate(res, l, r + 1, tmp + ")", n);
}
}
}
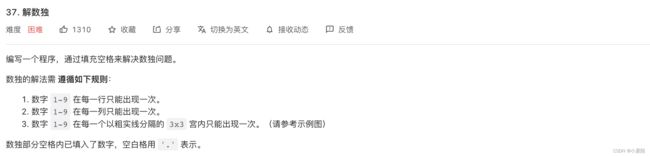
37. 解数独
题目解析：用回溯模板加位运算解决即可。
代码如下：
/**
* 回溯 + 位运算
*/
class Solution {
// 储存每一行存在的数字
private int[] line = new int[9];
// 储存 每一列存在的数字
private int[] column = new int[9];
// 储存每一个 3*3 宫存在的数字
private int[][] block = new int[3][3];
// 这个布尔数组用来判断是否填完所有空格
private boolean valid = false;
// 这个list用来记录所有空格的位置，整数数组第一个位置为行的位置 ，第二个位置为列的位置
private List spaces = new ArrayList();
public void solveSudoku(char[][] board) {
// 遍历所有位置
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
// 如果位置为空，我们把该位置加入spaces中
if (board[i][j] == '.') {
spaces.add(new int[]{i, j});
} else {
// 不为空则把该数字分别纳入对应的行，列，3*3宫中
int digit = board[i][j] - '0' - 1;
flip(i, j, digit);
}
}
}
// 开始搜索
dfs(board, 0);
}
public void dfs(char[][] board, int pos) {
// 如果spaces被遍历完了，说明我们填完了空格，将valid改为true，通过return结束这个函数
if (pos == spaces.size()) {
valid = true;
return;
}
// 获取第一个空格的位置
int[] space = spaces.get(pos);
// i，j分别为该空格的行数和列数
int i = space[0], j = space[1];
// |为or，通过3个或运算我们可以得到一个9位的二进制数字，从右到左分别代表1-9这个9个数是否可以填入该空格，通过~运算（取反），我们用1表示该数字是一个可填入的选项，0x1ff为十六进制 ，等同于111111111）
int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;
// 当mask不为0并且 valid为false表示还有数待填入，继续这个循环，mask &= (mask - 1)把最低位的1变为0
for (; mask != 0 && !valid; mask &= (mask - 1)) {
// 这个操作只保留最低位的1
int digitMask = mask & (-mask);
// 最低位的1后面的位数，digitMask-1将原本1后面的0全部变为了1
int digit = Integer.bitCount(digitMask - 1);
// 更新行，列，宫
flip(i, j, digit);
// 把该数填入板中
board[i][j] = (char) (digit + '0' + 1);
// 继续搜索
dfs(board, pos + 1);
// 撤回操作（原理是flip中的~运算，两个 1则为0,0表示这个位置代表的1-9中的那个数 不再是一个可被填入的选项）
flip(i, j, digit);
}
}
public void flip(int i, int j, int digit) {
// ^代表异或，只有1个1的时候才为1。比如0011^1001=1010
// <<代表左移，比如 1<<2=4被加入到下面的三个数组中，在二进制4为100，意味着3这个数字被占用了
line[i] ^= (1 << digit);
column[j] ^= (1 << digit);
block[i / 3][j / 3] ^= (1 << digit);
}
}
39. 组合总和
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
public List> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);
List> res = new ArrayList<>();
List temp = new ArrayList<>();
helper(0,res,temp,candidates,0,target);
return res;
}
private void helper(int curr,List> res,List temp,int[] candidates,int n,int target){
// 1
if(curr == target){
res.add(new ArrayList<>(temp));
return;
}
// 2
for(int i = n;i 40. 组合总和 II
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
List> list=new ArrayList<>();
List path=new ArrayList<>();
public List> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
dfs(candidates,target,0);
return list;
}
private void dfs(int[] candidates, int target,int index){
if(target==0){
list.add(new ArrayList<>(path));
return;
}
for(int i=index;iindex&&candidates[i]==candidates[i-1]){
continue;
}
path.add(candidates[i]);
dfs(candidates,target-candidates[i],i+1);
path.remove(path.size()-1);
}
}
}
}
46. 全排列
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
public List> permute(int[] nums) {
List> res = new ArrayList<>();
List list = new ArrayList<>();
backtrack(res, list, nums);
return res;
}
public void backtrack(List> res, List list, int[] nums) {
// 1
if(list.size() == nums.length) {
res.add(new ArrayList(list));
return;
}
// 2
for(int num : nums) {
if(!list.contains(num)) {
// 2.1
list.add(num);
// 2.2
backtrack(res, list, nums);
// 2.3
list.remove(list.size() - 1);
}
}
}
}
47. 全排列 II
题目解析：用回溯模板解决，重点是去重，同层走过的就直接不走了，跳过。
代码如下：
/**
* 回溯法
*/
class Solution {
List> result = new ArrayList<>();
List path = new ArrayList<>();
public List> permuteUnique(int[] nums) {
boolean[] used = new boolean[nums.length];
Arrays.fill(used, false);
Arrays.sort(nums);
backTrack(nums, used);
return result;
}
private void backTrack(int[] nums, boolean[] used) {
// 1
if (path.size() == nums.length) {
result.add(new ArrayList<>(path));
return;
}
// 2
for (int i = 0; i < nums.length; i++) {
// 与前数相等且used[i - 1] == true，说明同⼀树枝nums[i - 1]使⽤过
// 与前数相等且used[i - 1] == false，说明同⼀树层nums[i - 1]使⽤过
// 如果同⼀树层nums[i - 1]使⽤过则直接跳过，所有可能，因为之前跑过一次了
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
// 如果同⼀树⽀nums[i]没使⽤过开始处理
if (used[i] == false) {
used[i] = true;// 标记同⼀树⽀nums[i]使⽤过，防止同一树支重复使用
// 2.1
path.add(nums[i]);
// 2.2
backTrack(nums, used);
// 2.3
path.remove(path.size() - 1);// 回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复
used[i] = false;
}
}
}
}
51. N 皇后
题目解析：用基于集合的回溯法解题。
代码如下：
/**
* 回溯法
*/
class Solution {
public List> solveNQueens(int n) {
List> solutions = new ArrayList>();
int[] queens = new int[n];
Arrays.fill(queens, -1);
Set columns = new HashSet();
Set diagonals1 = new HashSet();
Set diagonals2 = new HashSet();
backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
return solutions;
}
public void backtrack(List> solutions, int[] queens, int n, int row, Set columns, Set diagonals1, Set diagonals2) {
if (row == n) {
List board = generateBoard(queens, n);
solutions.add(board);
} else {
for (int i = 0; i < n; i++) {
if (columns.contains(i)) {
continue;
}
int diagonal1 = row - i;
if (diagonals1.contains(diagonal1)) {
continue;
}
int diagonal2 = row + i;
if (diagonals2.contains(diagonal2)) {
continue;
}
queens[row] = i;
columns.add(i);
diagonals1.add(diagonal1);
diagonals2.add(diagonal2);
backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
queens[row] = -1;
columns.remove(i);
diagonals1.remove(diagonal1);
diagonals2.remove(diagonal2);
}
}
}
public List generateBoard(int[] queens, int n) {
List board = new ArrayList();
for (int i = 0; i < n; i++) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[queens[i]] = 'Q';
board.add(new String(row));
}
return board;
}
}
52. N皇后 II
题目解析：用基于集合的回溯法解题。
代码如下：
/**
* 回溯法
*/
class Solution {
public int totalNQueens(int n) {
Set columns = new HashSet();
Set diagonals1 = new HashSet();
Set diagonals2 = new HashSet();
return backtrack(n, 0, columns, diagonals1, diagonals2);
}
public int backtrack(int n, int row, Set columns, Set diagonals1, Set diagonals2) {
if (row == n) {
return 1;
} else {
int count = 0;
for (int i = 0; i < n; i++) {
if (columns.contains(i)) {
continue;
}
int diagonal1 = row - i;
if (diagonals1.contains(diagonal1)) {
continue;
}
int diagonal2 = row + i;
if (diagonals2.contains(diagonal2)) {
continue;
}
columns.add(i);
diagonals1.add(diagonal1);
diagonals2.add(diagonal2);
count += backtrack(n, row + 1, columns, diagonals1, diagonals2);
columns.remove(i);
diagonals1.remove(diagonal1);
diagonals2.remove(diagonal2);
}
return count;
}
}
}
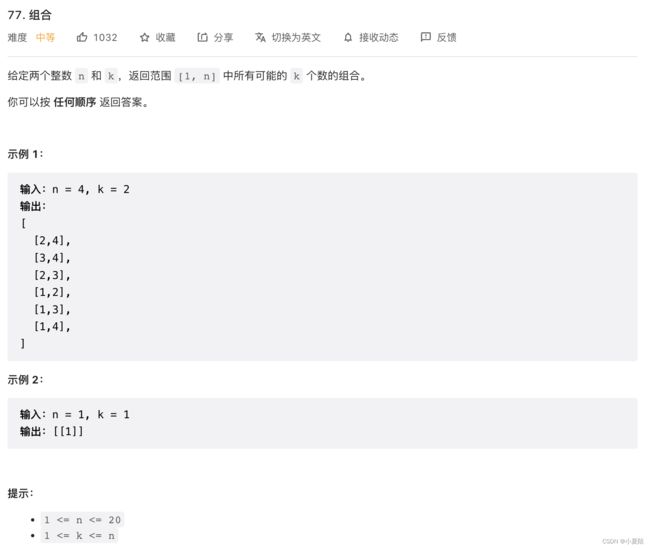
77. 组合
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
public List> combine(int n, int k) {
combineHelper(n, k, 1);
return result;
}
private void combineHelper(int n, int k, int startIndex){
//终止条件
// 1
if (path.size() == k){
result.add(new ArrayList<>(path));
return;
}
//2
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
// 2.1
path.add(i);
// 2.2
combineHelper(n, k, i + 1);
// 2.3
path.removeLast();
}
}
}
78. 子集
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
List> result = new ArrayList<>();// 存放符合条件结果的集合
LinkedList path = new LinkedList<>();// 用来存放符合条件结果
public List> subsets(int[] nums) {
if (nums.length == 0){
result.add(new ArrayList<>());
return result;
}
helper(nums, 0);
return result;
}
private void helper(int[] nums, int startIndex){
result.add(new ArrayList<>(path));// 遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合
if (startIndex >= nums.length){ // 终止条件可不加
return;
}
for (int i = startIndex; i < nums.length; i++){
path.add(nums[i]);
helper(nums, i + 1);
path.removeLast();
}
}
}
79. 单词搜索
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
public boolean exist(char[][] board, String word) {
if (board == null) {
return false;
}
// 该字母是否已遍历到
boolean[][] used = new boolean[board.length][board[0].length];
// 遍历所有坐标点，以作为起始点
for (int row = 0; row < board.length; row++) {
for (int column = 0; column < board[0].length; column++) {
// 找到则立即返回
if (helper(board, used, word, row, column, 0)) {
return true;
}
}
}
return false;
}
/**
* @param board 字母二维数组
* @param used 该字母是否使用表
* @param word 查找单词
* @param row 当前字母所在行
* @param column 当前字母所在列
* @param index 当前字母所在索引
* @return
*/
public boolean helper(char[][] board, boolean[][] used, String word, int row, int column, int index) {
// 超过边界、已使用过和与word不匹配，立即返回，不再进行其它操作
if (row < 0 || row >= board.length || column < 0 || column >= board[0].length
|| used[row][column] || board[row][column] != word.charAt(index)) {
return false;
}
// 1
// 查到最后一个字母，即查到该单词
if (index == word.length() - 1) {
return true;
}
// 2
// 2.1 添加状态
used[row][column] = true;
// 2.2 执行
boolean res = helper(board, used, word, row + 1, column, index + 1)
|| helper(board, used, word, row - 1, column, index + 1)
|| helper(board, used, word, row, column + 1, index + 1)
|| helper(board, used, word, row, column - 1, index + 1);
// 2.3 撤销状态
used[row][column] = false;
return res;
}
}
90. 子集 II
题目解析：用回溯模板解决，并用布尔数组去重。
代码如下：
/**
* 回溯法
*/
class Solution {
List> result = new ArrayList<>();// 存放符合条件结果的集合
LinkedList path = new LinkedList<>();// 用来存放符合条件结果
boolean[] used;
public List> subsetsWithDup(int[] nums) {
if (nums.length == 0){
result.add(path);
return result;
}
Arrays.sort(nums);
used = new boolean[nums.length];
subsetsWithDupHelper(nums, 0);
return result;
}
private void subsetsWithDupHelper(int[] nums, int startIndex){
result.add(new ArrayList<>(path));
// 1
if (startIndex >= nums.length){
return;
}
// 2
for (int i = startIndex; i < nums.length; i++){
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
continue;
}
// 2.1
path.add(nums[i]);
used[i] = true;
// 2.2
subsetsWithDupHelper(nums, i + 1);
// 2.3
path.removeLast();
used[i] = false;
}
}
}
93. 复原 IP 地址
题目解析：用回溯模板解决，这里难点在于需要把题抽象为树形结构，然后再用回溯法去解决，比较难想到。
代码如下：
/**
* 回溯法
*/
class Solution {
List result = new ArrayList<>();
public List restoreIpAddresses(String s) {
if (s.length() > 12) return result; // 算是剪枝了
backTrack(s, 0, 0);
return result;
}
// startIndex: 搜索的起始位置， pointNum:添加逗点的数量
private void backTrack(String s, int startIndex, int pointNum) {
if (pointNum == 3) {// 逗点数量为3时，分隔结束
// 判断第四段⼦字符串是否合法，如果合法就放进result中
if (isValid(s,startIndex,s.length()-1)) {
result.add(s);
}
return;
}
for (int i = startIndex; i < s.length(); i++) {
if (isValid(s, startIndex, i)) {
s = s.substring(0, i + 1) + "." + s.substring(i + 1); // 在str的后⾯插⼊⼀个逗点
pointNum++;
backTrack(s, i + 2, pointNum);// 插⼊逗点之后下⼀个⼦串的起始位置为i+2
pointNum--;// 回溯
s = s.substring(0, i + 1) + s.substring(i + 2);// 回溯删掉逗点
} else {
break;
}
}
}
// 判断字符串s在左闭⼜闭区间[start, end]所组成的数字是否合法
private Boolean isValid(String s, int start, int end) {
if (start > end) {
return false;
}
if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到⾮数字字符不合法
return false;
}
num = num * 10 + (s.charAt(i) - '0');
if (num > 255) { // 如果⼤于255了不合法
return false;
}
}
return true;
}
}
95. 不同的二叉搜索树 II
题目解析：单纯求个数，可用DP，但求过程则需要用回溯，这也是一种类型题，要注意。
代码如下：
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
/**
* 回溯法
*/
class Solution {
public List generateTrees(int n) {
return helper(1,n);
}
public List helper(int lo, int hi){
List res=new LinkedList<>();
// 1
if(lo>hi){
res.add(null);
return res;
}
// 2
for(int i = lo; i <= hi; i++){
List left = helper(lo, i-1);
List right = helper(i+1, hi);
for(TreeNode le : left){
for(TreeNode ri : right){
TreeNode root=new TreeNode(i);
root.left=le;
root.right=ri;
res.add(root);
}
}
}
return res;
}
}
126. 单词接龙 II
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
public List> findLadders(String beginWord, String endWord, List wordList) {
List> res = new ArrayList<>();
Set dict = new HashSet<>(wordList);
if (!dict.contains(endWord)) {
return res;
}
dict.remove(beginWord);
Map steps = new HashMap<>();
steps.put(beginWord, 0);
Map> from = new HashMap<>();
boolean found = bfs(beginWord, endWord, dict, steps, from);
if (found) {
Deque path = new ArrayDeque<>();
path.add(endWord);
dfs(from, path, beginWord, endWord, res);
}
return res;
}
private boolean bfs(String beginWord, String endWord, Set dict, Map steps, Map> from) {
int wordLen = beginWord.length();
int step = 0;
boolean found = false;
Queue queue = new LinkedList<>();
queue.offer(beginWord);
while (!queue.isEmpty()) {
step++;
int size = queue.size();
for (int i = 0; i < size; i++) {
String currWord = queue.poll();
char[] charArray = currWord.toCharArray();
for (int j = 0; j < wordLen; j++) {
char origin = charArray[j];
for (char c = 'a'; c <= 'z'; c++) {
charArray[j] = c;
String nextWord = String.valueOf(charArray);
if (steps.containsKey(nextWord) && steps.get(nextWord) == step) {
from.get(nextWord).add(currWord);
}
if (!dict.contains(nextWord)) {
continue;
}
dict.remove(nextWord);
queue.offer(nextWord);
from.putIfAbsent(nextWord, new HashSet<>());
from.get(nextWord).add(currWord);
steps.put(nextWord, step);
if (nextWord.equals(endWord)) {
found = true;
}
}
charArray[j] = origin;
}
}
if (found) {
break;
}
}
return found;
}
private void dfs(Map> from, Deque path, String beginWord, String cur, List> res) {
if (cur.equals(beginWord)) {
res.add(new ArrayList<>(path));
return;
}
for (String precursor : from.get(cur)) {
path.addFirst(precursor);
dfs(from, path, beginWord, precursor, res);
path.removeFirst();
}
}
}
131. 分割回文串
题目解析：用回溯模板解决，切割问题，可抽象为组合问题，这也是难想到的地方。
代码如下：
/**
* 回溯法
*/
class Solution {
List> lists = new ArrayList<>();
Deque deque = new LinkedList<>();
public List> partition(String s) {
backTracking(s, 0);
return lists;
}
private void backTracking(String s, int startIndex) {
// 如果起始位置大于s的大小，说明找到了一组分割方案
if (startIndex >= s.length()) {
lists.add(new ArrayList(deque));
return;
}
for (int i = startIndex; i < s.length(); i++) {
// 如果是回文子串，则记录
if (isPalindrome(s, startIndex, i)) {
String str = s.substring(startIndex, i + 1);
deque.addLast(str);
} else {
continue;
}
// 起始位置后移，保证不重复
backTracking(s, i + 1);
deque.removeLast();
}
}
// 判断是否是回文串
private boolean isPalindrome(String s, int startIndex, int end) {
for (int i = startIndex, j = end; i < j; i++, j--) {
if (s.charAt(i) != s.charAt(j)) {
return false;
}
}
return true;
}
}
216. 组合总和 III
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
public List> combinationSum3(int k, int n) {
helper(n, k, 1, 0);
return result;
}
private void helper(int targetSum, int k, int startIndex, int sum) {
// 减枝
if (sum > targetSum) {
return;
}
// 1
if (path.size() == k) {
if (sum == targetSum) result.add(new ArrayList<>(path));
return;
}
// 减枝 9 - (k - path.size()) + 1
//2
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
//2.1
path.add(i);
sum += i;
helper(targetSum, k, i + 1, sum);
// 2.2
//回溯
path.removeLast();
//回溯
sum -= i;
}
}
}
282. 给表达式添加运算符
题目解析：用回溯模板解决即可。
代码如下：
/**
* 回溯法
*/
class Solution {
int n;
String num;
int target;
List ans;
public List addOperators(String num, int target) {
this.n = num.length();
this.num = num;
this.target = target;
this.ans = new ArrayList();
StringBuffer expr = new StringBuffer();
backtrack(expr, 0, 0, 0);
return ans;
}
public void backtrack(StringBuffer expr, int i, long res, long mul) {
if (i == n) {
if (res == target) {
ans.add(expr.toString());
}
return;
}
int signIndex = expr.length();
if (i > 0) {
expr.append(0); // 占位，下面填充符号
}
long val = 0;
// 枚举截取的数字长度（取多少位），注意数字可以是单个 0 但不能有前导零
for (int j = i; j < n && (j == i || num.charAt(i) != '0'); ++j) {
val = val * 10 + num.charAt(j) - '0';
expr.append(num.charAt(j));
if (i == 0) { // 表达式开头不能添加符号
backtrack(expr, j + 1, val, val);
} else { // 枚举符号
expr.setCharAt(signIndex, '+');
backtrack(expr, j + 1, res + val, val);
expr.setCharAt(signIndex, '-');
backtrack(expr, j + 1, res - val, -val);
expr.setCharAt(signIndex, '*');
backtrack(expr, j + 1, res - mul + mul * val, mul * val);
}
}
expr.setLength(signIndex);
}
}
回到首页
刷 leetcode 500+ 题的一些感受
下一篇
《算法系列》之贪心