排序(Sort)(一)
文章目录
- 一、直接插入排序
-
- 1、步骤
- 2、思路
- 3、代码实现
- 4、特性总结
- 5、实现结果
- 二、希尔排序(缩小增量排序)
-
- 1、步骤
- 2、思路
- 3、代码实现
- 4、特性总结
- 5、实现结果
- 三、选择排序
-
- 1、步骤
- 2、思路
- 3、代码实现
- 4、特性总结
- 5、实现结果
- 四、堆排序
-
- 1、步骤
- 2、思想
- 3、代码实现
- 4、特性总结
- 5、实现结果
- 总结
一、直接插入排序
1、步骤
1、从一个元素开始,该元素默认为已排好序。
2、取其下一个元素tmp,从已排序的元素序列从后往前扫描。
3、如果该元素大于tmp,则将该元素移到下一位。
4、重复步骤3,直至遇到小于tmp的元素,排在其后面。
5、如果已排序所有元素都大于tmp,则将tmp插入到下标为0的位置。
6、重复2至5的步骤,直至结束。
2、思路
动态演示如下:
![]()
3、代码实现
单趟实现
void Insertsort(int* a, int n)
{
//先找到end的位置
int end = 0;
//保留end的下一值,防止其被覆盖而丢失
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
//end的值往后挪
a[end + 1] = a[end];
end--;
}
//这里运用break,在所有值全大于tmp的情况下也可以实现
else
{
break;
}
}
a[end + 1] = tmp;
}
多趟实现
void Insertsort(int* a, int n)
{
//这里i
for (int i = 0; i < n - 1; i++)
{
//先找到end的位置
int end = i;
//保留end的下一值,防止其被覆盖而丢失
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
//end的值往后挪
a[end + 1] = a[end];
end--;
}
//这里运用break,在所有值全大于tmp的情况下也可以实现
else
{
break;
}
}
a[end + 1] = tmp;
}
}
4、特性总结
1、时间复杂度:最好情况下:O(N),此时该排序为升序,或者接近升序;最坏情况下:O(N^2),此时为降序,或者说接近降序。
但时间复杂度综合情况下为O(N^2);
2、空间复杂度为O(1)。
3、稳定性:稳定。
5、实现结果
二、希尔排序(缩小增量排序)
1、步骤
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个
组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工
作。当到达=1时,所有记录在统一组内排好序。
2、思路
希尔排序,先将待排序列进行预排序,使待排序列接近有序,然后再对该序列进行一次插入排序,此时插入排序的时间复杂度为O(N)。
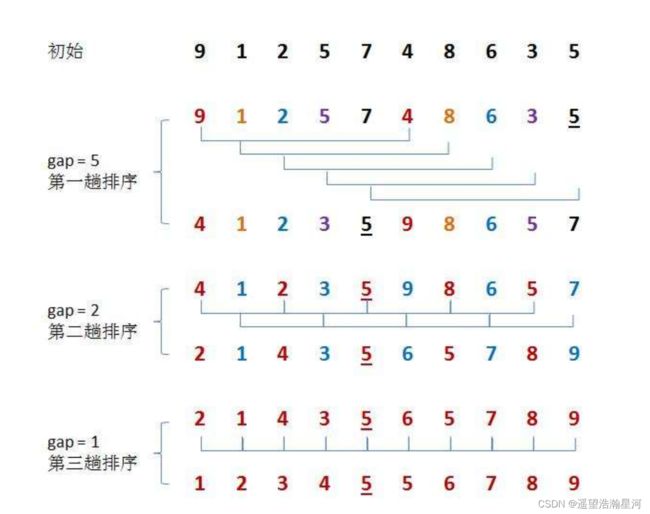
动图演示如下:
3、代码实现
void Shellsort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//+1是为了让最后gap为1,最后进行直接插入排序
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
4、特性总结
1、时间复杂度:O(N*logN),准确的大概来说是O(n^1.3)。
2、空间复杂度:O(1)。
3、希尔排序是对直接插入排序的优化
4、稳定性:不稳定 ,如将相同的值放进不同gap组内,会不稳定 例如 2,2,0,1,1,1。
5、实现结果
三、选择排序
1、步骤
每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完即可。
实际上,我们可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
2、思路
动态演示如下
![]()
3、代码实现
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int maxi = begin, mini = begin;
for (int i = begin + 1; i <= end; ++i)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[mini], &a[begin]);
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[maxi], &a[end]);
++begin;
--end;
}
}
4、特性总结
1、时间复杂度:O(N^2)
2、空间复杂度:O(1)
3、稳定性:不稳定 例如:2,2,0,1,9
5、实现结果
四、堆排序
1、步骤
1、建堆,堆分为大堆和小堆,建堆一般有向上建堆发和向下建堆法两种方法,一般推荐向下建堆,原因有二:1、效率高 2、排序运用到向下建堆法,可以不用建大堆来浪费时间。
2、排序,升序用大堆,降序用小堆。
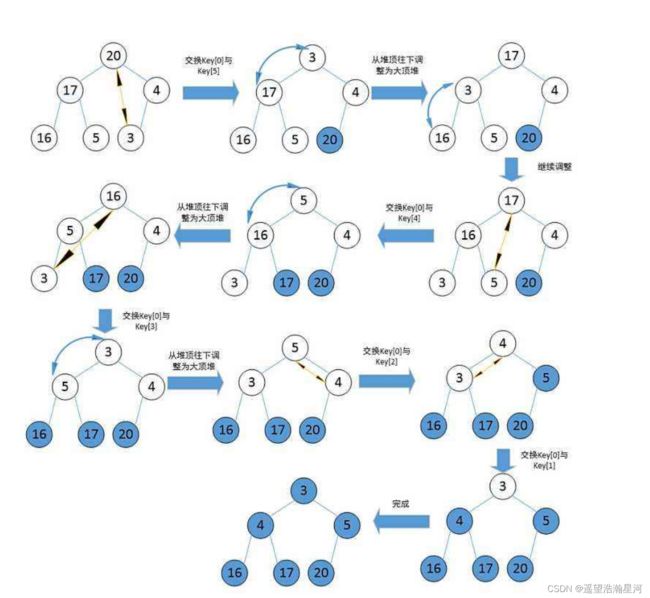
2、思想
3、代码实现
向上调整
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
向下调整
void AdjustDown(int* a, int n,int parent)
{
int child = parent * 2 + 1;
while (child<n)
{
//找出大的那个孩子
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
//继续往下调整
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
堆排序
void HeapSort(int* a, int n)
{
//向下调整建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//升序,大堆
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
--end;
}
}
4、特性总结
1、时间复杂度:O(N^2)。
2、空间复杂度:O(1)。
3、稳定性:不稳定 例如:8,8,8,1