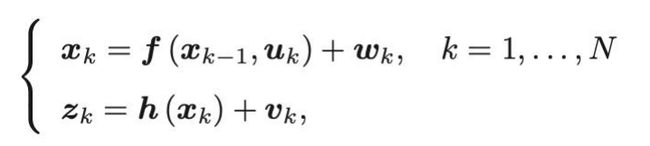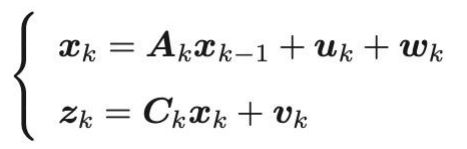五. 激光雷达建图和定位方案-算法工具
前面内容:
一. 器件选型心得(系统设计)--1_goldqiu的博客-CSDN博客
一. 器件选型心得(系统设计)--2_goldqiu的博客-CSDN博客
二. 多传感器时间同步方案(时序闭环)--1
三. 多传感器标定方案(空间同步)--1_goldqiu的博客-CSDN博客
三. 多传感器标定方案(空间同步)--2
三. 多传感器标定方案(空间同步)--3
四. 点云着色(真彩点云)方案
五. 激光雷达建图和定位方案-引言-CSDN博客
五. 激光雷达建图和定位方案-基础概念-CSDN博客
五. 激光雷达建图和定位方案-算法工具
滤波器理论回顾
在此之前我先讲讲对多传感器融合的理解:
在运动感知和环境感知上,即定位和环境感知上都需要多传感器融合技术;
至于定位上,我们主要是要估计出机器人或车辆在环境中的位姿,那么它作为状态变量的其中一大部分,需要在多传感器融合技术参与下,更高精度和更具有鲁棒性地估计出来;多传感器中有作为状态预测也有作为状态观测的,通过设计一个状态估计模型(滤波或者优化),将预测和观测信息结合起来通过批量优化或滤波递归的方式不断更新机器人的状态,主要就是融合多传感器预测和观测信息的不确定性或协方差或置信度,对状态进行一个评估、融合,估计得到一个更加高确定性、协方差更小、置信度更高的一个状态。
SLAM通常由运动方程和观测方程组成:
非线性形式
添加图片注释,不超过 140 字(可选)
线性形式
添加图片注释,不超过 140 字(可选)
线性形式的最优估计由卡尔曼滤波器给出。
对于一个SLAM问题来说,有运动方程和观测方程,运动方程为k时刻的运动状态,由上一时刻的运动状态以及状态转移矩阵,加上输入和噪声组成;观测方程为k时刻的观测,由k时刻的观测矩阵以及k时刻的运动状态,加上观测噪声组成。
状态由高斯分布描述:
预测:
添加图片注释,不超过 140 字(可选)
更新:
添加图片注释,不超过 140 字(可选)
卡尔曼滤波器的五个公式:
-
预测的状态= 状态转移矩阵乘上一时刻的状态(最优)+输入
-
预测的状态协方差 = 状态转移矩阵乘上一时刻的状态协方差(最优)+输入噪声 (因为有噪声的存在,所以在IMU预测过程中,状态协方差是不断增大的,即预测的状态信息是越来越不可信的)
P为状态协方差矩阵,R为输入噪声的协方差矩阵
3. 更新是更新卡尔曼增益K,K中包含观测矩阵和观测噪声协方差矩阵,以及预测的状态协方差矩阵
卡尔曼增益K,K中包含观测矩阵和观测噪声协方差矩阵,以及预测的下一时刻的状态协方差矩阵;即预测和观测的加权组合。
4. 下一时刻的状态包含观测和预测的加权组合。
下一时刻的状态X,包括卡尔曼增益、观测、观测矩阵、预测的下一时刻的状态矩阵,是观测和预测的加权组合(观测减去预测乘卡尔曼增益)。
5. 协方差矩阵P(也是下一时刻的),包括预测的协方差矩阵P,卡尔曼增益,观测矩阵(也是观测和预测的加权组合)
扩展卡尔曼滤波:
对非线性的运动方程或观测方程进行线性化,一阶泰勒展开。
迭代扩展卡尔曼滤波:
当非线性化程度比较强的时候,误差就会比较大;但是由于线性化的工作点离真值越近,线性化的误差就越小,就可以通过迭代来找到准确的线性化工作点,从而提高精度。
在这个情况下,后验协方差矩阵应该放到最后一步更新。
迭代的方法是重新做线性化;终止的条件是:两次的后验状态均值之间的差异小于一个阈值。
最优化和图优化
最简单的方法是梯度下降,即找一个初始值,沿着负梯度(非线性函数对求解参数进行求导)的方向逐步迭代,当迭代步长足够小时,即完成求解。
我们定义成数学问题,对于:
添加图片注释,不超过 140 字(可选)
我们的思路:
添加图片注释,不超过 140 字(可选)
ps:刚开始的时候,x1=x0 + ∆x0,k步后,xk + ∆xk
非线性优化问题的关键是如何确定∆x。
方法如下:
添加图片注释,不超过 140 字(可选)
方法1(最速下降法):步长不容易确定,容易陷入局部最优,根本原因是仅保留一阶项来近似求解。
方法2(牛顿法):求解Hessian矩阵的计算量比较大,且不容易求解。
方法3(高斯牛顿法):不是对lose-function进行泰勒展开,而是对非线性函数进行一阶泰勒展开,进行一阶线性化近似,然后构建目标函数,目标函数对∆x进行求导,最后求解线性方程组,用Jacobian来近似Hessian。这样的好处是收敛速度较快,特别适用于参数估计问题。然而,由于它基于二次函数的线性化,当目标函数存在较大的非线性特征时,可能会导致迭代过程中发散。
于是便引出LM法:
Levenberg-Marquardt方法:它是一种常用的非线性最小二乘优化算法,结合了最速下降法和高斯牛顿法的优点。它在高斯牛顿法的基础上引入了一个调整因子,以解决高斯牛顿法在目标函数具有较大非线性特征时可能出现的发散问题。
Levenberg-Marquardt法是在Gaussian-Newton法的基础上添加了阻尼因子λ,即求解线性方程:(H+λI)Ax=b
当λ较大时,相当于梯度下降法,而λ较小时,相当于G-N法。 当问题性质较好时,用高斯牛顿法,若问题接近病态,用LM法,稳定性更好,更容易收敛。
此外,我要强烈推荐深蓝学院的《自动驾驶与机器人中的SLAM技术》课程。我自己也从这门课程中受益匪浅。课程涵盖了现代自动驾驶和机器人领域中的Simultaneous Localization and Mapping (SLAM) 技术,这是实现车辆和机器人自主导航所必需的关键技术之一。深蓝学院的专业讲师团队深入浅出地讲解了SLAM的基本原理、常用算法以及实际应用,无论是初学者还是有一定经验的人都能够受益良多。如果您对移动机器人、自动驾驶或者SLAM技术有兴趣,这门课程绝对值得一试!
附上课程链接:
自动驾驶与机器人中的SLAM技术 - 深蓝学院 - 专注人工智能与自动驾驶的学习平台www.shenlanxueyuan.com/channel/Ye1vpH0Wd6/detail
期待我的后续分享,也希望能与更多热爱这一领域的小伙伴共同交流探讨。