数据结构与算法_【5】树和二叉树（C++实现）

参考：数据结构与算法基础（青岛大学-王卓）
传送门：
数据结构与算法_【1】概念引入（C++实现）
数据结构与算法_【2】线性表（顺序表链表）（C++实现）
数据结构与算法_【3】栈和队列（C++实现）
数据结构与算法_【4】串数组广义表（C++实现）
数据结构与算法_【5】树和二叉树（C++实现）
数据结构与算法_【6】树和森林（C++实现）
数据结构与算法_【7】哈夫曼树（C++实现）
数据结构与算法_【8】图（C++实现）
数据结构与算法_【9】查找（C++实现）
数据结构与算法_【10】排序（C++实现）

树和二叉树

数据的逻辑结构：

1 概念

1.1 树

树（Tree）是n（n>=0）个结点的有限集
若n = 0，称为空树；
若n > 0， 满足以下条件：
（1）有且仅有一个特定的称为根（Root）的结点
（2）其余结点可分为m（m>=0）个互不相交的有限集T1,T2,T3,…,Tm，其中每一个集合本身又是一棵树，并称为根的子树（SubTree）
注意： 树的定义是一个递归的定义
表示方式：嵌套集合，凹入表示，广义表

树的基本术语：
（1）根结点：非空树中无前驱结点的结点
（2）结点的度：结点拥有的子树数（分支、后继结点）
（3）树的度：树内各结点度的最大值
（4）叶子：终端节点，度=0
（5）分支结点：非终端结点，度！=0
（6）内部结点：根节点以外的分支结点
（7）孩子和双亲：结点的子树的根称为该节点的孩子，该结点称为孩子的双亲
（8）结点的祖先：从根到该结点所经分支上所有的结点
（9）结点的子孙：以某结点为根的子树中的任一结点
（10）树的深度：树中结点的最大层次
（11）有序树：树中结点的各子树从左到右有次序（最左边的为第一个孩子）
（12）无序树：树中结点的各子树无次序
（13）森林：是m（m>=0）棵互不相交的树的集合；树一定是一个森林，森林不一定是树！

线性结构： 第一个数据元素无前驱；最后一个元素无后继；其他数据元素一个前驱，一个后继，一对一；
树结构： 第一个数据元素（根节点）无双亲；最后一个元素（叶子结点）可以有多个，无孩子；其他数据元素（中间结点），一个双亲，多个孩子，一对多；

1.2 二叉树

二叉树是n（n>=0）个结点的有限集，它或者是空集（n=0），或者是由一个根节点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。

特点：
（1）每个结点最多有俩孩子（二叉树中不存在度大于2的结点）
（2）子树有左右之分，次序不能颠倒！！！
（3）二叉树可以是空集合，根可以有空的左子树或空的右子树

注意： 二叉树不是树的特殊情况，他们是两个概念

二叉树的性质：
（1）在二叉树的第i层上至多有2^(i-1)个结点（i>=1）
（2）深度为k的二叉树至多有2^(k-1)个结点（k>=1）
（3）对任何一棵二叉树T，如果其叶子树为n0，度为2的结点数为n2，则n0=n2+1

满二叉树：
一棵深度为k且有2^(k-1)个结点的二叉树称为满二叉树
特点：（1）每一层上的结点数都是最大节点数（即每层都满）；（2）叶子结点全部在最底层
编号规则：从根节点开始，自上而下，自左而右；每一结点位置都有元素

完全二叉树：
深度为k的具有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时，称为完全二叉树。

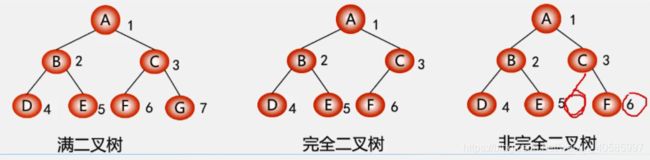
特征：
（1）叶子只可能分布在层次最大的两层上
（2）对任一结点，如果其右子树的最大层次为i，则其左子树的最大层次必为i或i+1
满二叉树一定是完全二叉树

完全二叉树性质：
（1）具有n个结点的完全二叉树的深度为log2(n)+1；知道结点数求深度
（2） 如果对一棵有n个结点的完全二叉树的结点按层序编号，则对任一结点i（1=

2 实现

2.1存储结构

顺序存储： 按满二叉树的结点层次编号，依次存放二叉树中的数据元素
顺序存储缺点： 最坏情况，深度为k的且只有k个结点的单支树需要长度为2^(k-1)的一维数组；浪费空间，适合存储满二叉树和完全二叉树

链式存储结构：
（1）二叉链表

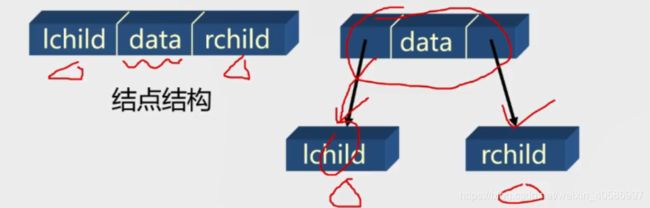
（2）三叉链表

2.2遍历二叉树

遍历定义：顺着某一条搜索路径巡访二叉树中的结点，使得每个结点均被访问一次，而且仅被访问一次。
遍历目的：得到树中所有结点的线性排列
遍历用途：它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心
遍历方法：

根据遍历序列确定二叉树：
（1）若二叉树中各结点的值均不相同，则二叉树结点的先序序列、中序序列和后序序列都是唯一的
（2）已知二叉树的先序和中序序列，构造出相应的二叉树
①由先序序列 确定根，由中序序列确定左右子树；②再分别在左子树、右子树中找出根、左子树、右子树序列；③以此类推
（3）由中序和后序确定二叉树
①由后序序列 确定根，由中序序列确定左右子树；②再分别在左子树、右子树中找出根、左子树、右子树序列；③以此类推

2.2.1先序遍历（递归）

2.2.2中序遍历（递归）

2.2.3后序遍历（递归）

2.2.4中序遍历非递归方法

2.2.5层次遍历

对于一颗二叉树，从根节点开始，按从上到下、从左到右的顺序访问每一个结点，每个节点仅仅访问一次。

思路：

2.3遍历算法应用

2.3.1 建立二叉树

2.3.2 计算二叉树深度

2.3.3 计算二叉树结点总个数

2.3.4 计算二叉树叶子结点数

2.4线索二叉树

例子：

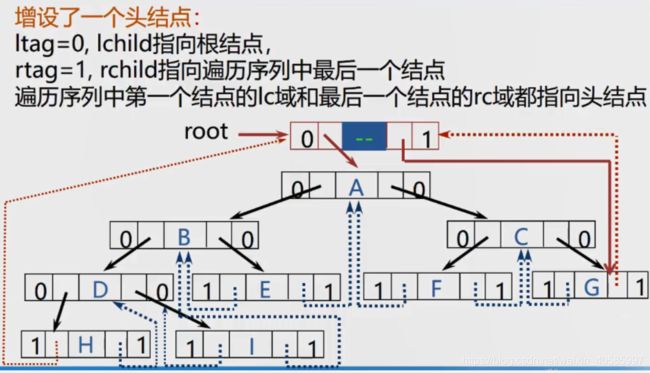
3 BinaryTree代码（类模板实现）

参考：【c++】构建一棵简单的二叉树

代码中所使用到的栈、队列等，在之前的笔记中已经给出。

#pragma once
#include
using namespace std;
#include"linkStack.hpp"
#include"seqQueue.hpp"


template<typename T>
class BinaryTree;

template<typename T>
class BinaryTreeNode {

	friend class BinaryTree<T>;
private:
	BinaryTreeNode<T>* _left;//左子树
	BinaryTreeNode<T>* _right;//右子树
	T _data;//数据
public:
	BinaryTreeNode(T data )
	{
		this->_left = NULL;
		this->_right = NULL;
		this->_data = data;
	}
	BinaryTreeNode(){}//默认构造

};


template<typename T>
class BinaryTree {
private:
	BinaryTreeNode<T>* _root;//根结点

public:
	BinaryTreeNode<T>* _MakeTree(const T* a, size_t size, int& index, const T& invalid);//构造函数使用的递归函数
	BinaryTreeNode<T>* CopyTree(const BinaryTreeNode<T>* _root);//拷贝构造使用的递归函数
	void _PreOrder(BinaryTreeNode<T>* _root);//前序遍历使用的递归函数
	void _InOrder(BinaryTreeNode<T>* _root);//中序遍历使用的递归函数
	void _PostOrder(BinaryTreeNode<T>* _root);//后序遍历使用的递归函数
	void Destroy(BinaryTreeNode<T>* _root);//析构函数使用的递归函数
	int _Depth(BinaryTreeNode<T> *_root);//计算二叉树深度所用的递归函数
	int _NodeCount(BinaryTreeNode<T>* _root);//计算二叉树结点总数递归函数
	int _LeafCount(BinaryTreeNode<T>* _root);//计算二叉树叶子结点数递归函数

public:
	BinaryTree(const T* a, size_t size, int index, const T& invalid);//构造函数
	BinaryTree(const BinaryTree<T>& t);//拷贝构造函数
	BinaryTree() {}//默认构造

	void PreOrder();//前序遍历
	void InOrder();//中序遍历
	void PostOrder();//后序遍历

	void PreOrderTraverse();//非递归前序遍历,使用栈
	void InOrderTraverse();//非递归中序遍历

	void LevelOrder();//层次遍历，使用队列

	int Depth();//计算二叉树深度
	int NodeCount();//计算二叉树结点总数递归函数
	int LeafCount();//计算二叉树叶子结点数(叶子结点指左右子树都为空的结点)

	~BinaryTree();//析构函数
	

};

template<typename T>
BinaryTreeNode<T>* BinaryTree<T>::_MakeTree(const T* a, size_t size, int& index, const T& invalid)
{
	/*
	递归：当我们从数组读取到一个数据时，我们先要判断这个值是不是合法，
	如果合法则new出一个结点并初始化作为当前结点，
	此时，进入左孩子递归函数读取下一个数据（++index），
	并把这个函数的返回值链到当前结点root的left，
	同理，将右孩子递归函数的返回值链到当前结点的right。
	如果不合法则return，返回上一层函数。最后我们会得到一个根节点
	注：以什么的样的顺序建树，就以什么样的顺序传参，事先要约定好。NULL用非法值代替
	这里用的是先序建树！！！
	*/

	BinaryTreeNode<T>* root = NULL;//先定义一个指向空的指针
	if (index < size && a[index] != invalid)
	{
		root = new BinaryTreeNode<T>(invalid);//给root指针分配内存，默认无效结点
		root->_data = a[index];
		root->_left = _MakeTree(a, size, ++index, invalid);
		root->_right = _MakeTree(a, size, ++index, invalid);
	}
	return root;
}


template<typename T>
BinaryTree<T>::BinaryTree(const T* a, size_t size, int index, const T& invalid)
{
	//T类型的指针a，传参时传一个数组，负责传入数据。size保存数组a的大小，
	//index记录下标，invalid表示非法值。
	this->_root = _MakeTree(a, size, index, invalid);

}

template<typename T>
BinaryTreeNode<T>* BinaryTree<T>::CopyTree(const BinaryTreeNode<T>* _root)
{
	if (_root == NULL)
	{
		return NULL;
	}
	else
	{
		BinaryTreeNode<T>* root = new BinaryTreeNode<T>(_root->_data);//给root指针分配内存，并存入数据
		root->_left = CopyTree(_root->_left);
		root->_right = CopyTree(_root->_right);
		return root;

	}
}

template<typename T>
BinaryTree<T>::BinaryTree(const BinaryTree<T>& t)
{
	//也要运用递归函数
	_root = CopyTree(t._root);

}

template<typename T>
int BinaryTree<T>::_Depth(BinaryTreeNode<T> *_root)
{
	if (_root == NULL)
	{
		return 0;
	}
	else
	{
		int m = _Depth(_root->_left)+1;
		int n = _Depth(_root->_right)+1;
		return m > n ? m : n;
	}
}

template<typename T>
int BinaryTree<T>::Depth()
{
	return _Depth(this->_root);
}

template<typename T>
int BinaryTree<T>::_NodeCount(BinaryTreeNode<T>* _root)
{
	if (_root == NULL)
	{
		return 0;
	}
	else
	{
		return _NodeCount(_root->_left) + _NodeCount(_root->_right) + 1;
	}

}

template<typename T>
int BinaryTree<T>::NodeCount()
{
	return _NodeCount(this->_root);
}

template<typename T>
int BinaryTree<T>::_LeafCount(BinaryTreeNode<T>* _root)
{
	if (_root == NULL)
	{
		return 0;
	}

	if (_root->_left == NULL && _root->_right == NULL)
	{
		return 1;
	}
	else
	{
		return _LeafCount(_root->_left) + _LeafCount(_root->_right);
	}

}


template<typename T>
int BinaryTree<T>::LeafCount()
{
	return _LeafCount(this->_root);
}

template<typename T>
void BinaryTree<T>::_PreOrder(BinaryTreeNode<T>* _root)
{
	if (_root == NULL)
	{
		return;
	}
	else
	{
		cout << _root->_data << " " << endl;
		_PreOrder(_root->_left);
		_PreOrder(_root->_right);
		return;
	}

}


template<typename T>
void BinaryTree<T>::PreOrder()
{
	_PreOrder(_root);//递归遍历
}


template<typename T>
void BinaryTree<T>::_InOrder(BinaryTreeNode<T>* _root)
{
	if (_root == NULL)
	{
		return;
	}
	else
	{
		_InOrder(_root->_left);
		cout << _root->_data << " " << endl;
		_InOrder(_root->_right);
		return;
	}
}

template<typename T>
void BinaryTree<T>::InOrder()
{
	_InOrder(this->_root);//递归遍历
}

template<typename T>
void BinaryTree<T>::_PostOrder(BinaryTreeNode<T>* _root)
{
	if (_root == NULL)
	{
		return;
	}
	else
	{
		_PostOrder(_root->_left);
		_PostOrder(_root->_right);
		cout << _root->_data << " " << endl;
		return;

	}
}

template<typename T>
void BinaryTree<T>::PostOrder()
{
	_PostOrder(_root);
}


template<typename T>
void BinaryTree<T>::PreOrderTraverse()
{
	BinaryTreeNode<T>* p = this->_root;
	LinkStack<BinaryTreeNode<T>> S;
	if (p == NULL)//二叉树中无结点
	{
		return;

	}
	while (p || !S.StackEmpty())
	{
		if (p)
		{
			S.Push(*p);
			cout << p->_data << endl;
			p = p->_left;
		}
		else
		{
			BinaryTreeNode<T> tem;
			S.Pop(tem);

			p = tem._right;
		}

	}

}


template<typename T>
void BinaryTree<T>::InOrderTraverse()
{
	BinaryTreeNode<T>* p = this->_root;
	LinkStack<BinaryTreeNode<T>> S;
	if (p==NULL)//二叉树中无结点
	{
		return;

	}

	while (p || !S.StackEmpty())
	{
		if (p)
		{
			S.Push(*p);
			p = p->_left;
		}
		else
		{
			BinaryTreeNode<T> tem;
			S.Pop(tem);
			cout << tem._data << endl;
			p = tem._right;
		}

	}

}


template<typename T>
void BinaryTree<T>::LevelOrder()
{
	BinaryTreeNode<T>* b = this->_root;//定义指针p指向二叉树头结点
	BinaryTreeNode<T> *dequ = new BinaryTreeNode<T>;//定义一个二叉树结点，接受出队的结点
	SeqQueue<BinaryTreeNode<T>>* qu = new SeqQueue<BinaryTreeNode<T>>;//初始化一个队列
	qu->EnQueue(*b);
	while (!qu->QueueEmpty())
	{

		qu->DeQueue(*dequ);
		cout << dequ->_data << endl;
		if (dequ->_left != NULL)
		{
			qu->EnQueue(*dequ->_left);
		}
		if (dequ->_right != NULL)
		{
			qu->EnQueue(*dequ->_right);
		}

	}

}

template<typename T>
void BinaryTree<T>::Destroy(BinaryTreeNode<T>* _root)
{

	BinaryTreeNode<T>* tmp = _root;
	if (tmp == NULL)//如果根结点为空，则不需要delete，直接return。
		return;
	Destroy(tmp->_left);
	Destroy(tmp->_right);
	delete tmp;
	tmp = NULL;

}

template<typename T>
BinaryTree<T>::~BinaryTree()
{
	//也要用到递归！！！
	Destroy(_root);

}