最短路问题
本文用到了Dijkstra算法和Floyd算法，要想了解这两种算法可看Floyd算法和Dijkstra算法
目录
一、最短路问题简述
二、求定点间的最短距离（Dijkstra算法）
1、Dijkstra(笛卡斯特拉）算法（1959年）原理
2、符号说明
3、Dijkstra算法步骤（标号法）
步骤1：
步骤2：
步骤3：
步骤4：
案例1
【符号设置】
【求解流程】
【求解结果】
三、求任意两点之间的最短路径（Floyd算法）
【算法步骤】
步骤1：
步骤2：
步骤3：
案例2
【符号设置】
【计算流程】
编辑
【计算结果】
四、最短路径的线性规划方法
【问题分析】
【符号设置】
【建立模型】
【数学模型】
案例3
案例4：设备更新问题
【模型假设】
【符号设置】
【问题分析】
【数学模型】
编辑
【计算结果】
一、最短路问题简述
最短路问题是网络理论中应用最广泛的问题之一，许多优化问题：比如设备更新，管道铺设、线路安排，工厂布局，运输线路安排等，都可以转化为最短路问题。
最短路问题有两种叙述：
（1）指定图中两点s,t，求连接s和t的链μ的权和最小，即
（2）求图G的任意两点之间的最短距离，为求解其它问题作铺设。
二、求定点间的最短距离（Dijkstra算法）
设G=(V,E)为连通图，赋权矩阵为A，vs和vn是图的两个顶点，μ是连接vs,vn的一条链，求使得链上所有边的权和最小的链，称为连接vs,vn的最短路径。数学模型为
1、Dijkstra(笛卡斯特拉）算法（1959年）原理
若{vs,v1,v2,…,vn-1,vn}是连接vs,vn的最短路径，则{vs,v1,…,vn-1}是连接vs,vn-1的最短路径。
2、符号说明
- V为顶点集合
- E为边集
- vs为起点v
- vn为终点
- p(vi)为vs到vi的最短距离,i=s,1,…,n。
3、Dijkstra算法步骤（标号法）
步骤1：
初始化参数：距离初始化：p(vs)=0,t(vi)=+∞,i=1,2,…,n；
步骤2：
设vi是刚刚得到p标号的点，计算
步骤3：
比较所有标t标号的点，把最小值的改为p标号，即
若有几个同时最小，都改为标号p；
步骤4：
用vk0替代vi重复步骤2-步骤3，直到所有点都改为p标号。
案例1
用笛杰斯特拉算法求图1中v1到v8的最短距离。
【符号设置】
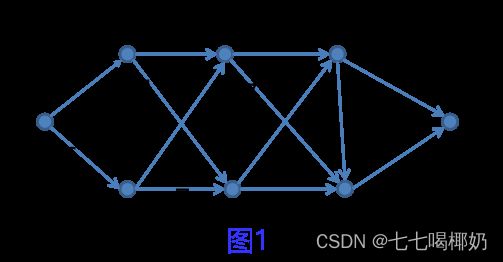
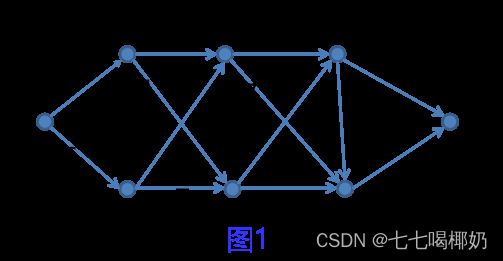
- d=d(i,j)8×8； 图1的权矩阵；
- p=[0,∞,∞,∞,∞,∞,∞,∞,∞]：各顶点的p标号初始值；
- t=[0,∞,∞,∞,∞,∞,∞,∞,∞]：各顶点t标号的初值；
- (u,v):起点为u，终点为v的边，(u,v)∈E；
- yu : 记录计算顶点的顺序；
【求解流程】
【求解结果】
按照以上流程编写matlab程序，计算得到表1
d=zeros(8,8);
d(1,2)=4;d(1,3)=6;d(2,4)=5;d(2,5)=4;
d(3,4)=4;d(3,5)=7;d(4,6)=9;d(4,7)=7;
d(5,6)=5;d(5,7)=6;d(6,7)=5;d(6,8)=4;d(7,8)=1;
p=inf*ones(1,8);p(1)=0;t=p;
r=1;yu=zeros(1,8);yu(1)=1;u=1;
while r<8
v=find(d(u,:)>0);
nv=length(v);
for k=1:nv
t(v(k))=min(t(v(k)),p(u)+d(u,v(k)));
end
pinf=find(p==inf);
mu=min(t(pinf));
dm=find(t==mu);
p(dm)=mu;
u=dm(1);
r=r+1;
yu(u)=u;
end
表1 各点到1的最短距离
| 顶点编号(yu) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 到1的最短距离(p) |
0 |
4 |
6 |
9 |
8 |
13 |
14 |
15 |
三、求任意两点之间的最短路径（Floyd算法）
有些问题，比如运输问题、网络布局问题、旅游路线规划问题，需要计算任意两点的最短路径，可用前面的Dijkstra算法，但点比较多时，就比较繁琐，下面介绍Floyd算法（1962年）可求出任意两点之间的最短距离。
【算法步骤】
步骤1：
输入权矩阵D(0)=D;
步骤2：
计算
步骤3：
中(i,j)元素就是vi,vj的最短距离。
案例2
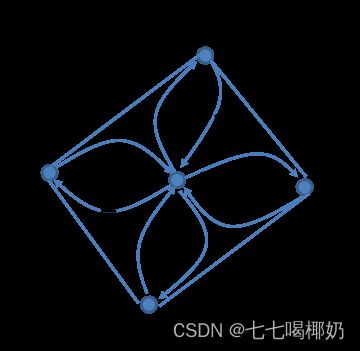
求图中所示G的任意两点之间的最短距离。
【符号设置】
D：网络权矩阵D=(dij)n×n;
【计算流程】
【计算结果】
编写例2的Floyd算法的matlab程序，计算得到个点之间的最短距离存入表.
d=inf*ones(5,5);
d(1,2)=5;d(1,3)=1;d(1,4)=2;
d(2,1)=5;d(2,3)=10;d(2,5)=2;
d(3,1)=2;d(3,2)=3;d(3,4)=2;d(3,5)=8;
d(4,1)=2;d(4,3)=6;d(4,5)=4;
d(5,2)=2;d(5,3)=4;d(5,4)=4;
for k=1:5
d(k,k)=0;
end
for k=1:5
for k1=1:5
for k2=1:5
d(k1,k2)=min(d(k1,k2),d(k1,k)+d(k,k2));
end
end
end
| 始点u\终点v |
1 |
2 |
3 |
4 |
5 |
| 1 |
0 |
4 |
1 |
2 |
6 |
| 2 |
5 |
0 |
6 |
6 |
2 |
| 3 |
2 |
3 |
0 |
2 |
5 |
| 4 |
2 |
6 |
3 |
0 |
4 |
| 5 |
6 |
2 |
4 |
4 |
0 |
四、最短路径的线性规划方法
【问题分析】
在图G=(V,E)中，求起点vs到终点vt的一条最短路。设vs到vt的最短路径所在链为L，对E中每条边(u,v)来说，它要么在L上，要么不在L上，因此可以设置变量：
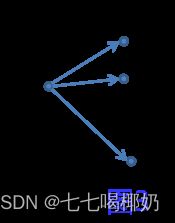
- 如图3所示，起点为vs，与之相连的边有k条，有且仅有一条边在L上；
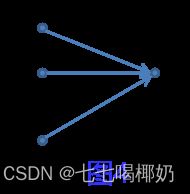
- 如图4所示，终点为vt，与之相连的边有k条，有且仅有一条边在L上；
- 如图5所示，若点u不在L上，则边(vi,u)都不在L上，（u,vj)也不在L上；
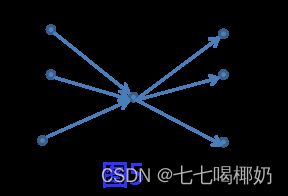
- 如图5所示，若u在L上，以u为终点的k条边只有一条边在L上；以u为起点的m条边也只有一条边在L上。
【符号设置】
- G=(V,E,D)：给定网络图,V为顶点集，E为边集, D为距离的权矩阵；
- Vs：最短路径起点；
- Vt：最短路径的终点；
- （u,v)：E中的边；
- d(u,v)；边(u,v)的权（距离）；
- L：连接vs和vt的最短路径；
【建立模型】
- 如图3所示，针对起点vs，有
- 如图4所示，针对终点vt，有
- 如图5所示，针对中间点u，有
- 目标：L链的权（距离）和
- 其它约束：
【数学模型】
案例3
求如图1所示的v1到v8的最短距离。
（步骤如上）
编写Lingo模型，计算得到最优解为：
x(v1,v2)=1;
x(v2,v5)=1;
x(v5,v7)=1;
x(v7,v8)=1.
sets:
dian/v1 v2 v3 v4 v5 v6 v7 v8/:;
bian(dian,dian)/v1,v2 v1,v3 v2,v4 v2,v5 v3,v4 v3,v5
v4,v6 v4,v7 v5,v6 v5,v7 v6,v7 v6,v8 v7,v8/:x,d;
endsets
data:
d=4 6 5 4 4 7 9 7 5 6 5 4 1;
enddata
min=@sum(bian:d*x);
@for(bian:@bin(x));
@sum(bian(i,j)|i#eq#1:x(i,j))=1;
@sum(bian(i,j)|j#eq#8:x(i,j))=1;
@for(dian(k)|k#ne#1#and#k#ne#8:
@sum(bian(k,j):x(k,j))=@sum(bian(i,k):x(i,k)));
v1到v8最短路径为v1-v2-v5-v7-v8,距离为15.
案例4：设备更新问题
张先生打算购买一辆新轿车，轿车的售价12万人民币，轿车购买后，每年的各种保险、养护费等如表1.如果5年内，张先生将轿车售出，并购买新车，5年内的二手车销售价格如表2。请帮助张先生设计一种购买轿车方案，使5年内用车的总费用最少。
表1 轿车的维护费用
| 车龄/年 |
0 |
1 |
2 |
3 |
4 |
| 费用/万元 |
2 |
4 |
5 |
9 |
12 |
表2 二手车的售价
| 车龄/年 |
1 |
2 |
3 |
4 |
5 |
| 费用/万元 |
7 |
6 |
2 |
1 |
0 |
【模型假设】
张先生任何一年年初都可以卖掉旧车买新车；
- 只是计算当前5年内的费用。
【符号设置】
- Cij表示第i年年初到第j-1年结束(第j年年初)的购车总消费
- Cij=在第i年开始到第j-1年的结束的轿车维护费用 +第i年开始购买新车的购买费-在第j-1年年末卖出二手车的销售收入
- xij 表示第i年年初购买新车，第j年年初（j-1年年末）换车，
其中，i=1,2,3,4,j=2,3,4,5,6.
【问题分析】
(凡是设备更新问题，均可以化为最短路径问题)
由于跨越5年，用6个点表示每个年的起始。用任意两点的连线表示从起点到终点所包含的年的花费，这样就构成了汽车消费费用网络图，如图5所示。
权系数的计算
C12=12+2-7=7,
C13=12+2+4-6=12,
C14=12+2+4+5-2=21,
C15=12+2+4+5+9-1=31,
同理，有
C16=12+2+4+5+9+12-0=44,
C23=7,C24=12,C25=21,C26=31,
C34=7,C35=12,C36=2
C45=7,C46=12,
C56=7,
将所计算数据反映在网络图如下
【数学模型】
【计算结果】
X(1,3)=1 x(3,4)=1 x(4,6)=1
即先用两年，再换车用一年，再换车用两年。最小费用为31万。