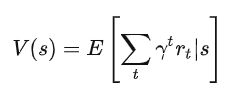强化学习基础（1）- 理论和算法

目录

1.基本概念

1.1组成部分

1.2 马尔可夫决策过程

2 有模型强化学习

2.1状态值函数

2.2动作值函数

2.3二者关系

2.4 探索和利用

2.5动态规划（DP）（有模型求解方法）

2.5.1预测任务

2.5.1控制任务

3.无模型强化学习

3.1 Value-Based

3.1.1蒙特卡洛法

3.1.2时序差分法

3.1.2.1 SARSA和Q-Learning

3.2 Policy-Based

3.2.1概念

3.2.2 Policy Gradient

3.2.3深度强化学习

3.3 Actor and Critic

4.主要算法

往期文章

参考文献

---

1.基本概念

1.1组成部分

      以吃豆人（Agent）游戏为例，游戏目标把屏幕里面所有的豆子全部吃完，同时又不能被幽灵碰到，被幽灵碰到则游戏结束。Agent每走一步、每吃一个豆子或者被幽灵碰到，屏幕左上方的分数（都会发生变化，图例中当前分数是435分。

• Agent（智能体）：强化学习训练的主体就是Agent，该游戏中Agent为吃豆人。
• Environment（环境）：整个游戏的大背景就是环境；吃豆人、幽灵、豆子以及里面各个隔离板块组成了整个环境。
• State（状态）：当前 吃豆人移动一下，幽灵也会移动，豆子数目也在会变化，也就是说，吃豆人发生一个动作，环境就会发生变化。
• Action（行动）：基于当前的状态，吃豆人可以采取哪些动作，比如向左or右，向上or下。
• Reward（奖励）：吃豆人在当前状态下，采取了某个的动作后，会获得环境的一定反馈就是奖励，在游戏中直观的表现就是分数的变化。

1.2 马尔可夫决策过程

      强化学习的训练过程可以简单理解为马尔可夫决策过程（MDP）。

MDP核心思想：下一步的State只和当前的状态State以及当前状态将要采取的Action有关，只回溯一步。

马尔可夫决策过程组成部分：

2 有模型强化学习

      假若 P和 R 已知，这就是基于模型的强化学习（Model-based RL），可以利用动态规划(DP)来求解最优策略。为了求解最优策略引入值函数的概念，而值函数又分为状态值函数和动作值函数。

2.1状态值函数

状态值函数：评价状态，用函数 来表示，其定义为：

      上述公式表示在状态 s下未来累积回报的期望，期望越大说明当前状态越有利，在AlphaGo里面就用来衡量当前棋局的落子情况对白方/黑方的有利程度，衡量了谁最后会胜出。

2.2动作值函数

动作值函数：评价当前状态下的动作，用函数 来表示，其定义为：

       上述公式表示了在状态 s下采取动作 a的累积回报，在AlphaGo里面就表示当前棋局状态下采取不同落子的动作对应的回报。

       补充解释：比方说，本科毕业你可以选择工作或者读研，那么工作和读研就是两种状态，对这两种状态进行评价（长期的回报），就叫做状态值函数。如果说，你读研之后，选择了计算机或者物理学，这就是当前状态下的动作选择，对该动作评价（长期的回报），就叫做动作值函数。

     一般来讲，如果可以获得最优，那么我们的策略选择就可以贪婪地采用最优动作：

2.3二者关系

2.4 探索和利用

        实际我们在进行强化学习训练过程中，会遇到一个“EE”问题。这里的Double E是“Explore & Exploit”，“探索&利用”。比如在Value-Based中，如下图StateA的状态下，最开始Action1&2&3对应的Value都是0，因为训练前我们根本不知道，初始值均为0。如果第一次随机选择了Action1，这时候StateA转化为了StateB，得到了Value=2，系统记录在StateA下选择Action1对应的Value=2。如果下一次Agent又一次回到了StateA，此时如果我们选择可以返回最大Value的action，那么一定还是选择Action1。因为此时StateA下Action2&3对应的Value仍然为0。Agent根本没有尝试过Action2&3会带来怎样的Value。
 

所以在强化学习训练的时候：

      一开始会让Agent更偏向于探索Explore，并不是哪一个Action带来的Value最大就执行该Action，选择Action时具有一定的随机性，目的是为了覆盖更多的Action，尝试每一种可能性。
      等训练很多轮以后各种State下的各种Action基本尝试完以后，我们这时候会大幅降低探索的比例，尽量让Agent更偏向于利用Exploit，哪一个Action返回的Value最大，就选择哪一个Action。

2.5动态规划（DP）（有模型求解方法）

  假设知道P 和R，就可以实现利用动态规划来完成预测和控制任务。

      预测任务的输入是和策略  ，目的是为了评估当前策略  的好坏，即求解状态值函数 ，注意这里上标指的是当前的策略对应的状态值函数；控制任务的输入是，目的是为了寻找最优策略 和 。

2.5.1预测任务

      利用上面 Q和 V 关系的公式，很容易得到 V 的迭代公式：

      那么在评估任务中，上述公式里面的 P,R, 都是已知的，只要迭代求解 V 即可，求解过程即上述迭代方程也称为贝尔曼期望方程（Bellman Expectation Equations）。

2.5.1控制任务

      对于control任务，由于 和 V都是未知的，可采用两种方法

策略迭代（Policy Iteration）：先进行策略评估（Policy Evaluation），即固定住 ，使用上述预测任务的做法来求解最优值函数 V ，再进行策略提升（Policy Improvement），可以简单地 利用贪婪算法找到最优策略，重复交替进行评估和提升，即可得到最优解。

值迭代（Value Iteration）：利用的是下面的公式：

两种方法分析：

总结：贝尔曼方程用在预测任务中，只用求解V即可，贝尔曼最优方程，是在V的基础上找到最优和 。

      以下图为例，白色圆圈表示状态，根节点是当前状态，当前状态下可以通过来选取动作，黑色实心点表示动作，采取某个动作又会根据 转移到不同的状态 ，故利用树动态规划可以得到贝尔曼期望方程和贝尔曼最优方程。

3.无模型强化学习

      此时P和R是未知的，只有智能体和环境交互后才能得到。

3.1 Value-Based

基于价值（动作）(Value-Based )：

      解释1：是输出所有可能的下一步动作的价值，我们会根据最高价值来选择动作。简单来说，选择当前State下对应Value最大的Action。强调一点这里面的Value并不只是从当前State进入下一个State的Action，还包括当前Action对未来的一系列影响的Reward。

      解释2：假设StateA状态下，可以采取的Action有3个，但是Action2带来的Value最大，所以最终Agent进入StateA状态时，就会选择Action2。（强调一点这里面的Value值，在强化学习训练开始时都是不知道的，我们一般都是设置为0。然后让Agent不断去尝试各类Action，不断与环境交互，不断获得Reward，然后根据我们计算Value的公式，不停地去更新Value，最终在训练N多轮以后，Value值会趋于一个稳定的数字，才能得出具体的State下，采取特定Action，对应的Value是多少）。

算法：Q-Learning、SARSA（State-Action-Reward-State-Action）

适用场景：Action空间是离散的，比如吃豆子里面的动作空间是“上下左右”，但有些Agent的动作空间是一个连续的过程，比如机械臂的控制，整个运动是连续的。如果强行要将连续的Action拆解为离散的也是可以的，但是得到的维度太大，往往是指数级的，不适宜训练。

      Value-Based有两种经典的方法，一种是蒙特卡洛法（MC），一种是时间差分法（TD）。

3.1.1蒙特卡洛法

蒙特卡洛法（MC）：

      在当前状态 下，想获得当前状态的，该怎么办呢？从当前状态 开始模拟运行（即采样一些运行轨迹），直到最终状态，计算这些轨迹（Trajectories）的评价累积回报，然后使 尽可能与  接近，那么采用更新策略：

      上述MC运行过程有两个需要注意的地方：第一，采样的轨迹必须到最终状态，因此上述得到的  是对 的无偏估计，但是由于轨迹比较长，会产生方差累积的情况，因而方差比较大；第二，模拟运行的策略选择是有多种方法的，不同的策略构成不同的算法，比方Q-learning和SARSA。一般是采用当前学习到的策略+探索得到的策略来模拟运行。

3.1.2时序差分法

时序差分法（TD）：

      它是在当前状态模拟运行一步，而不是模拟到最终状态，因此其更新策略为：

      TD是利用立即回报和下一状态的值函数的和  作为指导来学习的过程，前面的指导被称为TD-Target。TD因为只采样一步，因而效率比较高，但是TD-Target是有偏的，但是方差小。

总结：蒙特卡洛法得到的值函数是无偏估计，但是由于轨迹比较长，会产生方差累积的情况，时序差分法因为只采样一步，因而效率比较高，但是值函数是有偏的，但是方差小。

3.1.2.1 SARSA和Q-Learning

      两个算法基于的公式很类似，都是将上述介绍的TD里面的 V 换成Q 得到：

SARSA：

Q-Learning：

3.2 Policy-Based

3.2.1概念

       Value-Based方法适用于离散空间，但在连续空间中存在一些问题。

问题1：对于不连续的动作，这两种方法都可行，但如果是连续的动作（机械臂控制）基于价值的方法是不能用的，如果强行要将连续的Action拆解为离散的也是可以的，但是得到的维度太大，往往是指数级的，不适宜训练。我们只能用一个概率分布在连续动作中选择特定的动作。

问题2：随机策略（Stochastic policy）的学习比较困难，在基于值的强化学习里面得到的是  ，给定一个状态 s ，选择的策略是确定性的，不适合于那些最优策略就是随机策略的问题，比如石头剪刀布的最优策略是以(1/3, 1/3, 1/3）的概率来选择石头/剪刀/布。

      Policy Based的强化学习可以解决以上问题。

概念（Policy-Based）：

      解释1：是强化学习中最直接的一种，它能够感官分析所处的环境（状态），直接输出采取下一步各种行动的概率，然后根据概率采取行动，所有每种行动都可能被采用，只是可能性不同。          解释2：基于每个State可以采取的Action策略，针对Action策略进行建模，学习出具体State下可以采取的Action对应的概率，然后根据概率来选择Action。
      具体解释：

总结：基于值的强化学习目的在于学习到，然后获得贪心策略，当作最优策略；而基于策略的强化学习的目的就是对策略建模 。假如利用了上面的Softmax，实际上还是得到了一个策略 ，实际上已经不是基于值的强化学习了。

3.2.2 Policy Gradient

策略梯度-Policy Gradient - 知乎

3.2.3深度强化学习

      在上面介绍Value-based RL时，针对连续动作空间，可以转而使用Policy-based RL；对于很大的状态空间，比如Atari游戏的每一帧是一个状态，AlphaGo所要面对的围棋棋局的状态，这些状态空间太大，使用 来记录状态值函数需要很大的存储空间。所以引入值函数近似（Value Function Approximation），目的是

      在学习到Q 或者 V之后，就可以将其代入TD-Learning等等算法求解最优策略。当然值函数近似可以采用的近似方法有很多，比如线性函数近似、决策树近似、神经网络近似等等。最为常用的是线性函数近似和神经网络函数近似。现在基本都是神经网络。

3.3 Actor and Critic

概念：

Advantage Function：

补充1：关于Actor-Critic，像上面一样加了个Advantage就得到A2C算法，如果再加一个异步操作Asynchronous就得到了A3C。

补充2：

      立即回报：当前动作作用于当前状态的回报。

      长期回报：当前动作对后续状态产生的影响带来的长期回报。

      贪婪算法：选择当前最大值（长期回报最大的选择）

      算法：优先选最大值，对于其他值也有一定选择概率。

4.主要算法

1、Q-learning

      Q-learning：Q-learning 是一种无模型、非策略的强化学习算法。它使用 Bellman 方程估计最佳动作值函数，该方程迭代地更新给定状态动作对的估计值。Q-learning 以其简单性和处理大型连续状态空间的能力而闻名。

2、SARSA

      SARSA：SARSA 是一种无模型、基于策略的强化学习算法。它也使用Bellman方程来估计动作价值函数，但它是基于下一个动作的期望值，而不是像 Q-learning 中的最优动作。SARSA 以其处理随机动力学问题的能力而闻名。

3、DDPG

      DDPG：是一种用于连续动作空间的无模型、非策略算法。它是一种actor-critic算法，其中actor网络用于选择动作，而critic网络用于评估动作。DDPG 对于机器人控制和其他连续控制任务特别有用。

4、A2C

      A2C（Advantage Actor-Critic）：是一种有策略的actor-critic算法，它使用Advantage函数来更新策略。该算法实现简单，可以处理离散和连续的动作空间。

5、PPO

      PPO（Proximal Policy Optimization）：是一种策略算法，它使用信任域优化的方法来更新策略。它在具有高维观察和连续动作空间的环境中特别有用。PPO 以其稳定性和高样品效率而著称。

6、DQN

      DQN（深度 Q 网络）：是一种无模型、非策略算法，它使用神经网络来逼近 Q 函数。DQN 特别适用于 Atari 游戏和其他类似问题，其中状态空间是高维的，并使用神经网络近似 Q 函数。

7、TRPO

      TRPO （Trust Region Policy Optimization）：是一种无模型的策略算法，它使用信任域优化方法来更新策略。它在具有高维观察和连续动作空间的环境中特别有用。

      TRPO 是一个复杂的算法，需要多个步骤和组件来实现。TRPO不是用几行代码就能实现的简单算法。

注：本文前三章主要参考 基于值和策略的强化学习入坑 - 知乎，第四章主要参考7个流行的强化学习算法及代码实现_Imagination官方博客的博客-CSDN博客

往期文章

1.强化学习基础（2）—常用算法总结-CSDN博客

参考文献

1.基于值和策略的强化学习入坑 - 知乎

2.强化学习入门这一篇就够了！！！万字长文_写Bug那些事的博客-CSDN博客 

3.如何用简单例子讲解 Q - learning 的具体过程？ - 知乎 

4.7个流行的强化学习算法及代码实现_Imagination官方博客的博客-CSDN博客