ISR实现RDN图像增强

图像增强作用

当谈到计算机视觉和图像处理时，分辨率是一个关键的概念。图像的分辨率决定了我们能够观察到的细节和质量。然而，有时候我们面临的是低分辨率图像，这可能是由于多种原因，包括传感器限制、图像传输和存储问题等。

对于深度学习领域，低分辨率图像通常不是一个好的出发点。深度学习模型通常需要更多的细节和信息来进行准确的识别、分类和分析。这就是超分辨率技术变得如此重要的原因。

在这篇文章中，我们将探讨超分辨率技术的应用以及它对深度学习训练和模型推理的潜在好处。我们将了解如何将低分辨率图像转化为高分辨率图像，以及这种转化对各种计算机视觉任务的影响。

随着深度学习模型的发展，超分辨率技术已经变得更加强大和普遍。这种技术不仅可以提高图像质量，还可以改善深度学习模型在各种应用中的性能。从对象检测到图像分类，超分辨率技术为计算机视觉领域带来了重大的影响。

ISR项目

这里介绍一个图像增强的github项目包括了使用Keras实现的不同的单图像超分辨率（ISR）的残差稠密网络，以及用于训练这些网络的内容和对抗损失组件的脚本。

github地址：https://github.com/idealo/image-super-resolution

实现的网络包括：

基于《Residual Dense Network for Image Super-Resolution》（Zhang等人，2018）描述的超级放大残差稠密网络。
基于《ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks》（Wang等人，2018）描述的具有残差的残差稠密网络。
基于《Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network》（SRGANS，Ledig等人，2017）描述的自定义鉴别器网络

安装

有两种安装Image Super-Resolution包的方法：

1.从PyPI安装ISR（推荐）：

pip install ISR

2.从GitHub源代码安装ISR：

git clone https://github.com/idealo/image-super-resolution
cd image-super-resolution
python setup.py install

用法

预测

加载图像并准备它：

import numpy as np
from PIL import Image

img = Image.open('data/input/test_images/sample_image.jpg')
lr_img = np.array(img)

加载预训练模型并运行预测

from ISR.models import RDN

rdn = RDN(weights='psnr-small')
sr_img = rdn.predict(lr_img)
Image.fromarray(sr_img)

大图像推理

为了在大图像上进行预测并避免内存分配错误，可以使用by_patch_of_size选项来进行预测，例如：

sr_img = model.predict(image, by_patch_of_size=50)

训练

创建模型

from ISR.models import RRDN
from ISR.models import Discriminator
from ISR.models import Cut_VGG19

lr_train_patch_size = 40
layers_to_extract = [5, 9]
scale = 2
hr_train_patch_size = lr_train_patch_size * scale

rrdn  = RRDN(arch_params={'C':4, 'D':3, 'G':64, 'G0':64, 'T':10, 'x':scale}, patch_size=lr_train_patch_size)
f_ext = Cut_VGG19(patch_size=hr_train_patch_size, layers_to_extract=layers_to_extract)
discr = Discriminator(patch_size=hr_train_patch_size, kernel_size=3)

创建Trainer对象，并传入所需的设置和模型（f_ext和discr是可选的）：

from ISR.train import Trainer
loss_weights = {
  'generator': 0.0,
  'feature_extractor': 0.0833,
  'discriminator': 0.01
}
losses = {
  'generator': 'mae',
  'feature_extractor': 'mse',
  'discriminator': 'binary_crossentropy'
}

log_dirs = {'logs': './logs', 'weights': './weights'}

learning_rate = {'initial_value': 0.0004, 'decay_factor': 0.5, 'decay_frequency': 30}

flatness = {'min': 0.0, 'max': 0.15, 'increase': 0.01, 'increase_frequency': 5}

trainer = Trainer(
    generator=rrdn,
    discriminator=discr,
    feature_extractor=f_ext,
    lr_train_dir='low_res/training/images',
    hr_train_dir='high_res/training/images',
    lr_valid_dir='low_res/validation/images',
    hr_valid_dir='high_res/validation/images',
    loss_weights=loss_weights,
    learning_rate=learning_rate,
    flatness=flatness,
    dataname='image_dataset',
    log_dirs=log_dirs,
    weights_generator=None,
    weights_discriminator=None,
    n_validation=40,
)

开始训练

trainer.train(
    epochs=80,
    steps_per_epoch=500,
    batch_size=16,
    monitored_metrics={'val_PSNR_Y': 'max'}
)

卷积神经网络（CNN）在图像超分辨率（SR）方面取得了巨大成功，并提供了分层特征。然而，大多数基于深度CNN的SR模型没有充分利用原始低分辨率（LR）图像的分层特征

RDN算法介绍

这项研究提出了一种新颖的图像超分辨率（SR）解决方案，即残差稠密网络（RDN），以应对SR领域的挑战。RDN的设计主要集中在充分利用图像中的分层特征，旨在提高性能并提供更清晰的超分辨率图像。

RDN的关键特点

1. 分层特征利用：RDN充分利用了来自卷积神经网络的各个层次的分层特征。这有助于更好地理解图像的不同部分，并为超分辨率提供更多信息。
2. 残差稠密块（RDB）：RDN引入了残差稠密块，这是一种密集连接的卷积层，用于提取图像的丰富局部特征。这有助于保留图像中的细节和纹理。
3. 连续内存（CM）机制：RDB允许前一个RDB的状态直接连接到当前RDB的所有层，从而形成了一个连续内存机制。这有助于信息的传递和共享，提高了网络的性能。
4. 局部特征融合：RDB中的局部特征融合机制用于自适应地学习来自前一个和当前局部特征的更有效信息。这有助于稳定更宽的神经网络的训练过程。
5. 全局特征融合：一旦获得了密集的局部特征，RDN使用全局特征融合机制，以一种整体的方式联合和自适应地学习全局分层特征。这有助于更好地理解图像的整体结构。

Residual Dense Network的结构

如下图所示，Residual Dense Network（RDN）是一种用于图像超分辨率的深度神经网络结构，包括四个主要部分：

• 浅特征提取网络（SFENet）
• 残差稠密块（RDBs） （下一节详细介绍）
• 稠密特征融合（DFF）
• 上采样网络（UPNet）

RDN的输入是低分辨率（LR）图像，用$I_{LR}$表示，输出是经过超分辨率处理后的图像，用$I_{SR}$表示。

• $I_{LR}$：低分辨率（LR）图像的输入
• $I_{SR}$：超分辨率（SR）处理后的输出

下面按照RDN的结构从左到右开始介绍结构

首先，我们使用两个卷积层来提取浅特征。第一个卷积层从$I_{LR}$输入中提取特征$F_{-1}$，第二个卷积层将$F_{-1}$进一步转化为$F_0$。这些浅特征将用于后续的处理，公式如下所示：

$$F_{-1}=H_{SFE1}(I_{LR})$$

其中$H_{S}FE1(\cdot )$表示卷积操作。$F_{-1}$然后用于进一步提取浅特征和全局残差学习，进一步得到

$$F_0=H_{SFE2}(F_{-1})$$

其中$H_{SFE2}(\cdot )$表示第二个浅特征提取层的卷积操作，并用作输入到残差稠密块。

接下来，进入到RDB中，RDN包含多个残差稠密块（RDBs），它们用于从浅特征中提取局部密集特征。每个RDB产生局部特征$F_d$，其中$d$表示第几个RDB。这些RDBs共同提取并丰富图像的特征，公式如下：

$$F_d=H_{RDB,d}(F_{d-1})=H_{RDB,d}(H_{RDB,d-1}(...(H_{RDB,1}(F_0))\cdots ))$$

其中$H_{RDB,d}$表示第d个RDB的操作。$H_{RDB,d}$可以是一系列操作的复合函数，如卷积和整流线性单元（ReLU）。

由于$F_d$是由第d个RDB完全利用块内的每个卷积层产生的，可以将Fd视为局部特征。

在使用一组RDB提取分层特征之后，模型进一步进行了稠密特征融合（DFF），其中包括全局特征融合（GFF）和全局残差学习（GRL）。

DFF充分利用来自所有前面层的特征进行融合，也就是结构图中的如下部分，用公式可以表示为

$$F_{DF}=H_{DFF}(F_{-1},F_0,F_1,\cdots ,F_D)$$

其中$F_{DF}$是通过使用复合函数$H_{DFF}$利用DFF的输出特征图。有关DFF的更多细节下一节将介绍。

最后在LR空间中提取局部和全局特征后，在HR空间中堆叠上采样网络（UPNet）。在UPNet中使用了ESPCN 网络结构，然后再接一个卷积层。最后

RDN的输出可以表示为

$$I_{SR}=H_{RDN}(I_{LR})$$

其中$H_{RDN}$表示RDN的函数。

下面对核心网络块详细介绍

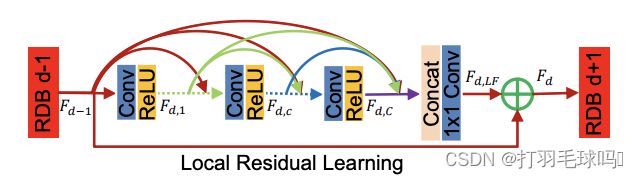
残差稠密块（Residual Dense Block）

残差稠密块如上图所示，下面将详细介绍提出的残差稠密块（RDB）。

RDB包含密集连接的层、局部特征融合（LFF）以及局部残差学习，从而实现连续内存（$CM$）机制。

连续内存机制是通过将先前的RDB状态传递给当前RDB的每一层来实现的。

让$F_{d-1}$和$F_d$分别表示第$d$个RDB的输入和输出，它们都具有$G_0$特征图。第$d$个RDB中的第c个卷积层的输出可以表示为

$$F_{d,c}=\sigma (W_{d,c}[F_{d-1},F_{d,1},\cdots ,F_{d,c-1}])$$

其中σ表示ReLU激活函数。$W_{d,c}$是$c-th$卷积层的权重，为简化起见省略了偏置项。假设$F_{d,c}$由$G$特征图组成。$[F_{d-1},F_{d,1},\cdots ,F_{d,c-1}]$是由第$(d-1)$个RDB产生的特征图、第d个RDB中的卷积层1、⋯、第$c-1$个RDB中的卷积层构成的拼接，从而得到$G_0+(c-1)\times G$特征图。先前的RDB和每一层的输出与所有后续层都有直接连接，这不仅保留了前馈性质，还提取了局部密集特征。

然后，就是局部特征融合（LFF）被应用于自适应融合来自前一个RDB的状态和当前RDB中的所有卷积层的信息，由$(d-1)$个RDB产生的特征图以拼接方式直接引入第$d$个RDB是必要的，以减小特征数量。另一方面，引入了一个$1\times 1$卷积层，以自适应控制输出信息。我们将这一操作命名为局部特征融合（LFF），表示为

$$F_{d,LF}=H_{LFF}^d([F_{d-1},F_{d,1},\cdots ,F_{d,c},\cdots ,F_{d,C}])$$

其中$H_{LFF}^d$表示第d个RDB中的$1\times 1$卷积层的函数

局部残差学习（LRL）在RDB中引入，以进一步改善信息流，因为在一个RDB中有多个卷积层。第d个RDB的最终输出可以通过以下方式获得

$$F_d=F_{d-1}+F_{d,LF}$$

稠密特征融合（Dense Feature Fusion）

在使用一组RDB提取局部密集特征后，进一步提出了稠密特征融合（DFF）以全局方式利用分层特征。DFF包括全局特征融合（GFF）和全局残差学习。全局特征融合旨在通过融合来自所有RDB的特征来提取全局特征FGF，表示为：

$$F_{GF}=H_{GFF}([F_1,\cdots ,F_D])$$

其中$[F_1,\cdots ,F_D]$表示由第1个至第D个残差稠密块产生的特征图的拼接。$H_{GFF}$是$1\times 1$和$3\times 3$卷积的复合函数。$1\times 1$卷积层用于自适应融合具有不同级别的特征。接下来的$3\times 3$卷积层用于进一步提取全局残差学习所需的特征.。

然后，利用全局残差学习来获得上采样之前的特征图

$$F_{DF}=F_{-1}+F_{GF}$$

其中$F_{-1}$表示浅特征图。在全局特征融合之前的所有其他层都充分利用了提出的残差稠密块（RDBs）。RDBs生成了多层局部密集特征，这些特征被进一步自适应融合以形成FGF。经过全局残差学习后，获得了稠密特征FDF。

，