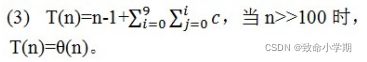【算法设计zxd】第四章蛮力法 1.枚举法 02穷举查找
目录
蛮力法(brute force):
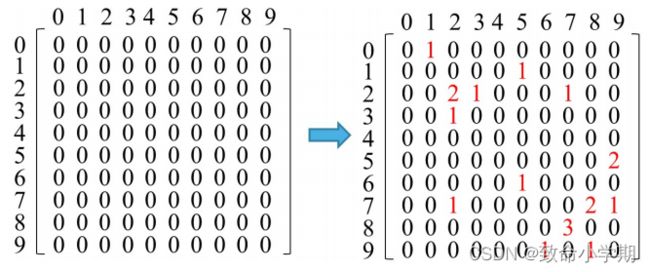
【例4-1】链环数字对
问题分析
计算模型
pair_digital(int n):
代码:
【例4-2】解数字迷:
思考题:ACM预测:
问题分析:
计算模型:
算法分析:
Assume():
代码
【例4-3】输出玫瑰矩阵,其为n*n的方阵,特征如下所示:
思考题:
算法2:
算法分析:
代码:
问题分析:
计算模型:
二、穷举查找
【例4-4】旅行商问题(traveling salesman problem,TSP)——排列树
有
问题分析
计算模型
代码:
1.蛮力字符比较
2.旅行路线 效率类型
3.城市个数
【例4-5】背包问题。——组合森林
问题分析
计算模型
图的搜索
思考题
1.广度优先 三壶问题
2.广度优先 迷宫最优解
代码00:队列
01:栈
02栈:
蛮力法(brute force):
【例4-1】链环数字对
问题分析
计算模型
| 算法设计与描述 | 算法分析 |
| 输入:n,x1,x2,....,xn | |
| 输出:有效数字对 | |
| pair_digital(int n): { int a[10,10] <- {0} ; input( x1 ); for( i<- 1; i { a[x1,x2] <- a[x1, x2]+1; x1<-x2; } for ( i<-0 ;i<10;i<-i+1 ) { for(j<-0 ;j<=i;j<-j+1) { if(a[i,j]!=0 and a[j,i]!=0) if(i!=j) output( (i,j) = a[i,j] , (j,i) =a[j,i ] ); else output( (i,j)=a[i,j]);//对角线元素 } } |
(1)输入n个元素,计数矩阵10*10 (2)核心语句包括两部分:统计和输出 当n>>100时,是上面的部分占比较大。 |
代码:
#include
using namespace std;
int main()
{
int n=20;
int x[n]={0, 1, 5, 9 ,8 ,7, 2 ,2 ,2 ,3, 2, 7 ,8, 7 ,8 ,7, 9, 6, 5 ,9};
int a[10][10]={0,0};
for(int i=0;i<10;i++)
{
for(int j=0;j<10;j++)
{
a[i][j]=0;
}
}
for(int i=1;i【例4-2】解数字迷:
问题分析
思考题:ACM预测:

问题分析:
甲乙丙丁四位学生取得名次4*3*2*1种可能,一共是n!种可能,但是在约束条件下只有一种可能是正确的。因此用多重循环对每种可能的情况进行遍历,当符合条件时跳出循环。
计算模型:
甲乙丙丁设为int a,b,c,d;所存数字代表名次。
(1)a可能的名次是从1到4, for(a=1;a<=4;++a)
(2)b可能的名次是从1到4,for(b=1;b<=4;++b),且不等于a的名次(b!=a),
(3)c可能的名次是从1到4,for(c=1;c<=4;++c),且不等于a,b的名次(c!=a&& c!=b)
(4)d可能的名次是除abc之外的剩下名次,也就是10-a-b-c;
(5)在此种可能下 若三位老师的预测都是一真一假 ((a==1)+(b==3)==1)&&( (c==1)+(d==4 )==1)&&((a==3)+(d==2)==1 ),则成立。
算法分析:
| 算法设计与描述 | 算法分析 |
| 输入:学生人数n,三位老师的预测 | |
| 输出:正确排名 | |
Assume():{ int a,b,c,d; } |
(1)输入人数 n=4, (2)核心语句:判断是否符合条件。 (3)最坏情况是每种情况都遍历。T(n)=n! |
代码
#include
using namespace std;
/*
ACM大赛预测计算名次
Z:甲第一,乙第三。
L:丙第一,丁第四。
T:丁第二,甲第三。
都只说对一半
计算名次
*/
int main()
{
//假设甲乙丙丁是ABCD
int a,b,c,d;
for(a=1;a<=4;++a)
{
for(b=1;b<=4;++b)
{
if(a!=b)
for(c=1;c<=1;++c)
{
d=10-a-b-c;
if(((a==1)+(b==3)==1)&&( (c==1)+(d==4 )==1)&&((a==3)+(d==2)==1 ) )
{
cout<<"甲:"< 【例4-3】输出玫瑰矩阵,其为n*n的方阵,特征如下所示:
问题分析:
左侧:a[j, i] <- k, k <- k+1, j <- j+1;
底侧:a[n-i-1, j] <- k, k <- k+1,j <- j+1;
右侧:a[j, n-i-1] <- k, k <- k+1,j <- j-1;
顶侧:a[i, j] <- k, k <- k+1,j <- j-1;
计算模型
设圈数为i,变化量为j,矩阵元素值为k且k <- 1
左侧:a[j, i] <- k, k <- k+1, j <- j+1; 其中,j∈[i, n-i-1)
底侧:a[n-i-1, j] <- k, k <- k+1, j <- j+1; 其中,j∈[i, n-i-1)
右侧:a[j, n-i-1] <- k, k <- k+1, j <- j-1; 其中,j∈[n-i-1, i)
顶侧:a[i, j] <- k, k <- k+1, j <- j-1; 其中,j∈[n-i-1, i)
圈数控制:i=n/2(取整),对于奇数项,最后一圈1个元素
思考题:
算法2:
下标
(0,0) (0,1) (0,2) (0,3)
(1,0) (1,1) (1,2) (1,3)
(2,0) (2,1) (2,2) (2,3)
(3,0) (3,1) (3,2) (3,3)
- index<- hc/i+1
- hc<- hc+1
- hc∈[1,2*i-1]
- s[index]<-s[index]+t
- a[s[1],s[0]]<- k , k<- k+1
- i<- i-1 ,t<- -t 当hc>2*i-1
算法分析:
| 算法设计与描述 | 算法分析 |
| 输入:输入规模为n*n | |
| 输出:类玫瑰矩阵 | |
| void RP(int n) } |
(1)输入规模n*n, (2)核心语句:半圈数据摆放。 (3)实际计算次数是k 也就是n*n T(n)=C*k =C*n*n = |
代码:
#include
using namespace std;
void RP(int n)
{
int s[2];
int a[n][n];
int k=1,i=n,t=1;
s[0]=-1,s[1]=0;
while(k<=n*n)
{
for(int hc=1;hc<=2*i-1;++hc)
{
int index=hc/(i+1);
s[index]=s[index]+t;
a[s[1]][s[0]]=k;
++k;
}
i--;
t=-t;
}
for(int i=0;i 问题分析:
n是矩阵边长。
用 i 表示圈 ,j代表圈内下标变化量:
顶侧:a[i,j]<-k ,k<- k+1 , j<- j+1 ;//横坐标不变 纵坐标++
右侧:a[j,n-i-1] ,k<- k+1 , j<- j-1 ;//纵坐标不变,横坐标--
底侧:a[i,j]<-k ,k<- k+1 , j<- j-1 ;//横坐标不变 纵坐标--
左侧:a[j,n-i-1] ,k<- k+1 , j<- j+1 ;//纵坐标不变,横坐标++
计算模型:
n是矩阵边长。
用 i 表示圈 ,j代表圈内下标变化量,矩阵元素k 且k<-1 .
顶侧:a[i,j]<-k ,k<- k+1 , j<- j+1 ;其中 j∈[ i,
右侧:a[j,n-i-1] ,k<- k+1 , j<- j-1 ;//纵坐标不变,横坐标--
底侧:a[i,j]<-k ,k<- k+1 , j<- j-1 ;//横坐标不变 纵坐标--
左侧:a[j,n-i-1] ,k<- k+1 , j<- j+1 ;//纵坐标不变,横坐标++
二、穷举查找
【例4-4】旅行商问题(traveling salesman problem,TSP)——排列树
问题分析
计算模型
(2)计算 设起始点下标为0
生成排列树。设解空间为a,则其解空间的计算过程可描述为:
求回路代价。设sumi 是并入第i个结点的代价 :
sumi并入第i个结点的代价= sum_i-1代入第i-1个结点的代价 + 边(i-1到i)
代码:
#include
using namespace std;
int n=4;
int edge[4][4]={0,8,5,4,
8,0,7,3,
5,7,0,1,
4,3,1,0};
int vertex[4]={'a','b','c','d'};
int a[]={0,1,2,3};//解空间
int minvalue=1000;//当前最小值
int path[4]={0};//当前解的路径
int minpath[4]={0};//最优解
void output(int a[])
{
for(int i=0;icost())//当前解的权值
{
minvalue=cost();//最小路径
cout<<"cost():"< 1.蛮力字符比较
蛮力字符匹配算法:
设T[0...n-1] ,P[0..m-1]
文本串的第一个字符 从模板串的第一个字符到最后一个字符进行比较,耗时m
若不成功,则从文本串第二个字符再开始 与模板串所有字符进行比较。
最坏情况下 需要n次比较,每次耗时m
T(n,m)=n*m=O(n*m);
2.旅行路线 效率类型
T(n)=O( (n-1)! )
3.城市个数
用太湖之光计算城市个数
每秒十亿次 10^10 十位数
1小时=60*60s=3.6*10^13 约15个城市
24小时= 24*3.6*10^13 =8.64*10^14 约16个城市
1年=365*8.64*10^14=3.1536*10^17 约19个
100年 =3.1536*10^19 约33个
【例4-5】背包问题。——组合森林
问题分析
(砍枝过程)
计算模型
图的搜索
邻接链表
思考题
1.广度优先 三壶问题
!!!终于做出来了,感谢zy
#include
using namespace std;
/*
一个8品
3 5
make 4
思想引导:
可以将每一种状态看做节点
然后广度优先,边遍历边建图
将每一个节点和他的状态前缀压到图容器里面,
然后遍历容器
走到其中有一个为四的时候从该节点开始依次前推得出整个路径
实际:
穷举+一点点回溯的感觉
*/
typedef struct node{
int x,y,z;
struct node * pre;
}node;
queueq;//队列
set h;
node *p2;
void show(node *p)
{
cout<<"("<x<<","<y<<","<z<<")"<x==4 || p->y==4 ||p->z==4)return true;
else return false;
}
void bfs()
{
node* p=new node;
p->x=8;p->y=0;p->z=0;//初始状态
p->pre=NULL;
//入队
q.push(p);
// node *p1;
while(!q.empty() )
{
//队首元素
node *p1=q.front();
if(pan(p1))return;//结束循环
int x=p1->x;
int y=p1->y;
int z=p1->z;
q.pop();
//当前状态是否被访问过
if(h.find(x*100+y*10+z) !=h.end())//找到
continue;//跳过
else h.insert(x*100+y*10+z);
// show(p1);
//进行尝试
//1.x->y
if(x>0 && y<5 )
{
p2=new node;
if(x+y>5)//会溢出
{
p2->x=(x + y -5);
p2->y=5;
}else
{
p2->x=0;
p2->y=y+x;
}
p2->z=z;
p2->pre=p1;
q.push(p2);
if(pan(p2))return;//结束
}
//x-z
if(x>0 && z<3)
{
p2=new node;
if(x+z>3)//会溢出
{
p2->x=(x+z-3);
p2->z=3;
}
else
{
p2->x=0;
p2->z=x+z;
}
p2->y=y;
p2->pre=p1;
q.push(p2);
if(pan(p2))return;//结束
}
//y-x
if(y>0 )
{
p2=new node;
p2->x=y+x;
p2->y=0;
p2->z=z;
p2->pre=p1;
q.push(p2);
if(pan(p2))return;//结束
}
//y-z
if(y>0 && z<3)
{
p2=new node;
if(y+z>3)//会溢出
{
p2->y=(y+z-3);
p2->z=3;
}
else
{
p2->y=0;
p2->z=y+z;
}
p2->x=x;
p2->pre=p1;
q.push(p2);
if(pan(p2))return;//结束
}
//z-x
if(z>0 )
{
p2=new node;
p2->z=0;
p2->x=x+z;
p2->y=y;
p2->pre=p1;
q.push(p2);
if(pan(p2))return;//结束
}
//z-y
if(z>0 && y<5)
{
p2=new node;
if(y+z>5)//会溢出
{
p2->y=5;
p2->z=(z+y-5);
}
else
{
p2->z=0;
p2->y=y+z;
}
p2->x=x;
p2->pre=p1;
q.push(p2);
if(pan(p2))return;//结束
}
}
}
int main()
{
bfs();
node *p=q.front();
cout<<"res:"<pre;
}
return 0;
}
/*
res:
(1,4,3)
(5,0,3)
(6,0,2)
(6,2,0)
(3,2,3)
(3,5,0)
(8,0,0)
*/ 2.广度优先 迷宫最优解
是否“广度优先第一个解就是最优解” ?
广度优先的遍历顺序也是决定因素之一,例如这个迷宫,如果是先向右下遍历 那么找到第一条应该就是最优解。
代码:队列(自)
#include
#include
#include
using namespace std;
//迷宫 队列
int m[10][10]={
1,1,1,1,1,1,1,1,1,1,
1,0,0,0,0,0,0,0,0,1,
1,0,1,1,1,1,0,1,0,1,
1,0,0,0,0,1,0,1,0,1,
1,0,1,0,0,0,0,1,0,1,
1,0,1,0,1,1,0,1,0,1,
1,0,1,0,0,0,0,1,1,1,
1,0,1,0,0,1,0,0,0,1,
1,0,1,1,1,1,1,1,0,1,
1,1,1,1,1,1,1,1,1,1,} ;
typedef struct po{
int x,y;
struct po * pre;//
}po;
//用链表存储路径
queue q;//队列
int fx[]={-1,1,0,0};//方向
int fy[]={0,0,-1,1};//方向
int x=1,y=1;//起点
po *p;
void bfs()//广度优先
{
m[x][y]=3;//已访问
p=new po;
p->x=x;
p->y=y;
p->pre=NULL;
q.push(p);//起点入队
while(!q.empty() )
{
po * p1=q.front();//队首元素
q.pop();
//对该结点进行尝试,共四种可能
for(int i=0;i<4;i++)
{
po* pnew=new po;
pnew->pre=NULL;
pnew->x =p1->x + fx[i];
pnew->y = p1->y+ fy[i];
//该点是否可以走
if(m[pnew->x][pnew->y] ==0 ) //未走过
{
m[pnew->x][pnew->y]=3;//已走过
//保存两点之间的关系
pnew->pre=p1;
q.push(pnew);//新结点入队
}
if(pnew->x==8 && pnew->y==8)//结束条件
return;//结束
}
}
}
int main()
{
bfs();
po * p=q.front();
while(p)
{
cout<x<<","<
y<pre;
}
return 0;
}
代码00:队列
#include
#include
#include
using namespace std;
/*
队列 先入先出
每次都是对最近的点也就是偏下偏右的点 进行遍历
因而更容易找到最短路径
*/
int maze[10][10]={
1,1,1,1,1,1,1,1,1,1,
1,0,0,0,0,0,0,0,0,1,
1,0,1,1,1,1,0,1,0,1,
1,0,0,0,0,1,0,1,0,1,
1,0,1,0,0,0,0,1,0,1,
1,0,1,0,1,1,0,1,0,1,
1,0,1,0,0,0,0,1,1,1,
1,0,1,0,0,1,0,0,0,1,
1,0,1,1,1,1,1,1,0,1,
1,1,1,1,1,1,1,1,1,1,} ;
//maze[x][y]=0表示通路,maze[x][y]=1表示墙,
//maze[x][y]=2表示“死”路,maze[x][y]=3表示已走过。
typedef struct place{
int x,y;
struct place *pre;
}place,*P;
void mazesearch_BFS()
{
queue q;
P p1,p2;
p1=(place *)malloc(sizeof(place));
p2=(place *)malloc(sizeof(place));
//行走的相对路径
int fx[4]={-1,1,0,0};//方向
int fy[4]={0,0,-1,1};//方向
int nextx=1,nexty=1;//起点
maze[nextx][nexty]=3; //起点已走过
//起点
p1->x=nextx;
p1->y=nexty;
p1->pre=NULL;
q.push(p1);//终点入队
//队列 先入先出
//
while(!q.empty()){
p2=q.front();//队首元素
cout<<"front:"<x<<" "<y<x==8 && p2->y==8){//终点
cout<<"@end"<x+fx[j];
nexty= p2->y+fy[j];
cout<<"is:"<x<<" "<y<x=nextx;
p3->y=nexty;
maze[nextx][nexty]=3;//标记已走过
cout<<"bis:"<x<<" "<y<pre=p2;//标记其前驱 即刚出队的点
cout<<"ais:"<x<<" "<y<x<<" "<y<<"@@@@"<pre->x<<" "<pre->y<x<<" "<y<<"@@@@"<x<<" "<y<x==8 && p2->y==8){//p2是终点
cout<<"("<x<<","<y<<")"<<" ";
while(p2->pre){
p2=p2->pre;
cout<<"("<x<<","<y<<")"<<" ";
}
}
}
int main()
{
mazesearch_BFS();
return 0;
}
/*
(8,8) (7,8) (7,7) (7,6) (6,6) (6,5) (6,4) (6,3) (5,3) (4,3) (3,3) (3,2) (3,1) (2,1) (1,1)
*/ 01:栈
#include
#include
#include
#include
using namespace std;
/*
用stack 后入先出
也就是每次都是对 左上 的点优先遍历
更多冤种路径
队列 先入先出
每次都是对最近的点也就是偏下偏右的点 进行遍历
因而更容易找到最短路径
*/
int maze[10][10]={
1,1,1,1,1,1,1,1,1,1,
1,0,0,0,0,0,0,0,0,1,
1,0,1,1,1,1,0,1,0,1,
1,0,0,0,0,1,0,1,0,1,
1,0,1,0,0,0,0,1,0,1,
1,0,1,0,1,1,0,1,0,1,
1,0,1,0,0,0,0,1,1,1,
1,0,1,0,0,1,0,0,0,1,
1,0,1,1,1,1,1,1,0,1,
1,1,1,1,1,1,1,1,1,1,} ;
//maze[x][y]=0表示通路,maze[x][y]=1表示墙,
//maze[x][y]=2表示“死”路,maze[x][y]=3表示已走过。
int fx[]={-1,1,0,0};
int fy[]={0,0,-1,1};
typedef struct p{
int x,y;
struct p* next;
}point;
void bfs()
{
stacks;
point *head=new point,*p;
int x=1,y=1;
head->x=x;
head->y=y;
head->next=NULL;
maze[x][y]=3;//已访问
s.push(head);
int flag=0;
while(!s.empty() )
{
p=s.top();
s.pop();
cout<<"front:"<x<<" "<y<y+fy[i];
x=p->x+fx[i];
if(maze[x][y]==0)
{
cout<x=x;
newp->y=y;
newp->next=p;
s.push(newp);
if(x==8 && y==8)
{
flag=1;
break;
}
}
}
if(flag)break;
}
p=s.top();
while(p)
{
cout<<"("<x<<","<y<<")"<<" ";
p=p->next;
}
}
int main()
{
bfs();
return 0;
}
/*
(8,8) (7,8) (7,7) (7,6) (6,6) (6,5) (6,4) (6,3) (5,3) (4,3) (4,4) (4,5) (4,6) (3,6) (2,6) (1,6) (1,5) (1,4) (1,3) (1,2) (1,1)
*/ 02栈:
#include
#include
#include
#include
using namespace std;
/*
用stack 后入先出
也就是每次都是对 左上 的点优先遍历
更多冤种路径
队列 先入先出
每次都是对最近的点也就是偏下偏右的点 进行遍历
因而更容易找到最短路径
当然 这是由上下左右搜索的顺序决定的
*/
int maze[10][10]={
1,1,1,1,1,1,1,1,1,1,
1,0,0,0,0,0,0,0,0,1,
1,0,1,1,1,1,0,1,0,1,
1,0,0,0,0,1,0,1,0,1,
1,0,1,0,0,0,0,1,0,1,
1,0,1,0,1,1,0,1,0,1,
1,0,1,0,0,0,0,1,1,1,
1,0,1,0,0,1,0,0,0,1,
1,0,1,1,1,1,1,1,0,1,
1,1,1,1,1,1,1,1,1,1,} ;
//maze[x][y]=0表示通路,maze[x][y]=1表示墙,
//maze[x][y]=2表示“死”路,maze[x][y]=3表示已走过。
int fx[]={0,0,-1,1};
int fy[]={-1,1,0,0};
typedef struct p{
int x,y;
struct p* next;
}point;
void bfs()
{
stacks;
point *head=new point,*p;
int x=1,y=1;
head->x=x;
head->y=y;
head->next=NULL;
maze[x][y]=3;//已访问
s.push(head);
int flag=0;
while(!s.empty() )
{
p=s.top();
s.pop();
cout<<"front:"<x<<" "<y<y+fy[i];
x=p->x+fx[i];
if(maze[x][y]==0)
{
cout<x=x;
newp->y=y;
newp->next=p;
s.push(newp);
if(x==8 && y==8)
{
flag=1;
break;
}
}
}
if(flag)break;
}
p=s.top();
while(p)
{
cout<<"("<x<<","<y<<")"<<" ";
p=p->next;
}
}
int main()
{
bfs();
return 0;
}
/*
01:(8,8) (7,8) (7,7) (7,6) (6,6) (6,5) (6,4) (6,3) (5,3) (4,3) (4,4) (4,5) (4,6) (3,6) (2,6) (1,6) (1,5) (1,4) (1,3) (1,2) (1,1)
02:(8,8) (7,8) (7,7) (7,6) (6,6) (6,5) (6,4) (6,3) (5,3) (4,3) (3,3) (3,2) (3,1) (2,1) (1,1)
*/ 裴蜀定理:
设 d=gcd(a,b) ,最大公约数
那么对于方程 ax+by=d,一定存在一组整数解。并且对于方程 ax+by=z,如果满足 z%d==0,那么方程一定有整数解,否则无整数解。
也就是若z是最大公约数的整数倍。
代码:
int gcd(int x,int y)
{
return y==0? x :gcd( y,x%y);
}
bool pan(int x,int y,int z)
{
return z==0 || (x+y>=z && gcd(x,y)==0 );
}当容量为x、y的两水壶可以获得z升的水,则有ax+by=z,其中a、b均为整数。证明:
以x=3,y=5为例,当有ax+by=z,a=-2,b=2,表示需要将壶2接满两次水,壶1满壶状态下倒空两次:将壶2接满第一次,有5升水;壶2倒入壶1,壶2剩余2升水,壶1第一次倒空;将壶2的水倒入壶1,壶1有2升水,壶2空;将壶2接满第二次;将壶2的水倒入壶1,壶2剩余4升水;将壶1第二次倒空;于是就剩下了壶2的4升水.