字符串匹配KMP算法及其时间复杂度分析

   字符串匹配算法是非常常见的算法。考虑长度为$n$的文本（text）字符串$A[1,2,\cdots ,n]$，长度为$m$的匹配（pattern）字符串$B[1,2,\cdots ,m]$，并且$m\le n$。暴力求解（brute-force）的匹配算法十分直接。将$B$逐位与$A$进行对比，直到$B$完全匹配$A$的某个子串。例如，先拿$B$与$A[1,2,\cdots ,m]$匹配，如果失败，尝试匹配$B$与$A[2,3,\cdots ,m+1]$，以此类推，直到匹配$B$与$A[n-m+1,\cdots ,n]$。该方法的时间复杂度为$O(mn)$，详细的分析可以参考参考文献[2]。
   Knuth, Morris和Pratt三人提出了时间复杂度为线性的KMP算法。该算法将时间复杂度从暴力求解的$O(mn)$降低为$O(n+m)$。下面详细讨论该算法，主要参考参考文献[1]。
   考虑下面的图示，其中文本字符串记为$T$，匹配字符串记为$P$。匹配字符串为$P{=}^{\prime }ababac{a}^{\prime }$。当匹配进行到(a)所示的这一步时，$P$相对于$T$移动了$s$位，并且前5位均能正确匹配，匹配失败在第6位。此时，$P[6]{=}^{\prime }{c}^{\prime }$，对应的$T[s+6]{=}^{\prime }{a}^{\prime }$。假如我们正在使用暴力求解算法，当前的匹配失败后，此时我们需要将$P$向右再移动移位，即总体相对于$T$移动$s+1$位，使得$P[1]{=}^{\prime }{a}^{\prime }$对准$T[s+2]{=}^{\prime }{b}^{\prime }$，开始新的匹配。显然，这样的匹配也是失败的，并且在第一位就失败了。于是，继续移动$P$，将它右移一位，使得$P[1]{=}^{\prime }{a}^{\prime }$对准$T[s+3]{=}^{\prime }{a}^{\prime }$，再次开始匹配。
   在观察上面的匹配过程的时候，我们发现，其实我们在$P$移动$s$位的这次匹配失败后，可以直接右移两位，而不是一位。右移两位是因为我们可以看到$T[s+2]{=}^{\prime }{a}^{\prime }=P[1]$，而移动移位之后对准的$T[s+1]$显然和$P[1]$不相等。这种移位，减少了不必要的匹配。

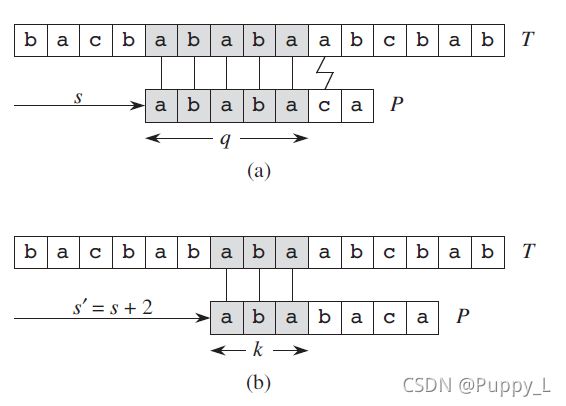
   在右移两位之后，开始新的匹配，如(b)所示，此时需要考虑一个问题，那就是我们还需要从第一位$P[1]$开始匹配吗？显然不是，从图中可以看出，$P[1,2,3]$已经和$T[s+3,s+4,s+5]$匹配好了，只需要从$P[4]$开始匹配。如此一来，相较于暴力求解，又减少了匹配次数。可问题是，我们怎么知道前几是匹配好了，然后从某个点开始新匹配呢？例如在(b)中，我们如何知道前3个点是匹配的，从而从第4个点开始匹配？显然，在(a)的匹配中，我们已经比较过$[s+3,s+4,s+5]$的值了，因此我们可以通过某种手段，将他们的信息储存起来，这种储存方式不一定是显性的，他可以是某种隐含地方式。
   为实现上面分析的想法，我们引入一个辅助（auxiliary）序列$\pi [1,2,\cdots ,m]$，他和$P$等长。辅助序列是实现上述算法思想的关键。从(a)到(b)的关键是需要知道$P[1]$和$T[s+1]$往后的元素中的哪一个是匹配的，我们就把$P$移动到$P[1]$与之对齐。在(a)中，匹配失败于$P[6]$，假如辅助序列的相邻位可以提供给我们信息，告诉我们现在可以右移2位，使得$P[1]$与$T[s+3]$是匹配的，那我们的想法就实现了。比如$\pi [5]$这个元素告诉我们可以右移2位，即$\pi [5]=2$。
   实际上，$\pi$中的元素$\pi [i]$表示的是在序列$B[1,2,\cdots ,i]$中，最多有前$\pi [i]$个元素和后$\pi [i]$个元素对应相等，即$B[1,2,\cdots ,\pi [i]]=B[i-\pi [i]+1,i-\pi [i]+3\cdots ,i]$。例如，上图中的$P$对应的$\pi$为$\pi =[0,0,1,2,3,0,1]$。有了$\pi$，我们再来看如何由(a)变到(b)。在(a)中，匹配于$P[6]$失败，于是我们查询其前一位的辅助序列元素$\pi [5]=3$。$\pi [5]=3$意味着$P[1,2,3]=P[3,4,5]$。此外，我们的匹配在$P[6]$失败，意味着之前的匹配是成功的，于是有$T[s+1,\cdots ,s+5]=P[1,\cdots ,5]$，结合$P[1,2,3]=P[3,4,5]$，于是有$P[1,2,3]=P[3,4,5]=T[s+3,s+4,s+5]$，于是我们需要将$P$右移$\pi [6-1]-1=2$位，使得$P[1,2,3]$与$T[s+3,s+4,s+5]$对齐。新的匹配从$P[4]$与$T[s+6]$开始。需要注意的是，从(a)到(b)，虽然$P$移位了，并且新的匹配点变成了$P[4]$，但是$T$的匹配点并没有变，仍然是$T[s+6]$。
   辅助序列$\pi$的生成算法如下。他的思想是，对于某个$\pi [q]$，$k=\pi [q-1]$，这意味着$P[1,2,\cdots ,k]=P[q-k+1,q-k+2,\cdots ,q]$。比较当前$P[k+1]$是否与$P[q]$匹配，如果匹配，则$\pi [q]=k+1$。如果不匹配，则寻找前面某个$k$，使得$P[k+1]=P[q]$。寻找前面的某个$k$，我们还得使匹配序列的长度尽量大，因此，令$k=\pi [k]$。

   KMP的主算法如下，它调用了上面的辅助序列生成算法，并且与辅助序列生成算法在形式上十分相似。

   下面分析KMP算法的时间复杂度。很多网上的博客都没有讲清楚其复杂度的分析，大多数点出用摊还（amortized）分析法，这里我们直接引用参考文献[2]的分析方法，简单易懂。由于KMP主算法的结构与序列生成算法几乎一样，所以我们分析序列生成算法的时间复杂度，KMP主算法的分析类似可得。
   序列生成算法的时间复杂度主要由第5行的for循环里面的内容决定。第10行的赋值，其时间复杂度是$O(m)$，这是显然的。剩下的需要分析的是第7行和第9行的执行次数。这两行均是对$k$的值进行改变，因此我们研究一下$k$的取值区间。在刚进入for循环的时候，$k$被赋值为0，而$q$被赋值为2。在for循环中，只有第9行执行的时候，$k$才增加1。而每一次for循环，$q$都会增加1。每次循环不一定执行第9行。于是，我们知道，整个算法中，都有$k<q\le m$。进一步，第10行赋值$\pi [q]=k$，因此，$\pi [q]<q$。换个符号，也等价于$\pi [k]<k$。所以，第7行的赋值意味着减小$k$。至此，我们知道，第7行减小$k$，第9行增加$k$，并且$k<q\le m$。因为第9行执行的次数最多为$m$，所以第7行执行的次数也不会超过$m$次。综上，序列生成算法中所有步骤的时间复杂度均是$O(m)$，所以算法的总时间复杂度就是$O(m)$。同理，KMP主算法的时间复杂度是$O(n)$，整个KMP算法的时间复杂度是$O(n+m)$。

参考文献

[1] Cormen T H, Leiserson C E, Rivest R L, et al，Introduction to algorithms，2009。
[2] 阮行止​，如何更好地理解和掌握 KMP 算法?，2020-02-23。