人群密度估计--论文阅读：DM-Count

1. 论文地址
2. GitHub开源代码地址

以下翻译主要为机翻，结合手工校对。

摘要

在人群计数中，每个训练图像包含多个人，每个人都用一个点标记。现有的人群计数方法需要使用高斯平滑每个带注释的点或估计给定带注释点的每个像素的可能性。在本文中，我们表明将高斯方法强加于注释会损害泛化性能。相反，我们建议使用分布匹配（Distribution Matching）进行人群计数（DM-Count）。在DM-Count中，我们使用最优传输（Optimal Transport）来测量归一化预测密度图和归一化GT密度图之间的相似度。为了稳定OT计算，我们在模型中包括了总变化（Total Variation）损失。我们证明，DM-Count的泛化误差范围比高斯平滑方法的泛化误差范围更严格。在平均绝对误差（MAE）方面，DM-Count在两个大型计数数据集（UCF-QNRF和NWPU）上大大优于以前的最新方法，并在ShanghaiTech和UCF-CC50数据集上获得了最新结果。 DM-Count将最新发布结果的误差降低了约16％。

一. 介绍

基于图像的人群计数是一个重要的研究问题，在包括新闻和监控在内的许多领域中都有各种应用。当前最先进的方法[54、8、25、55、61、59、17、48、21、23、36]将人群计数视为密度图估计问题，其中深度神经网络首先会产生一个给定输入图像的2D人群密度图，随后通过对密度图所有空间位置上的密度值求和来估算人群的总大小。对于大量人群的图像，该密度图估计方法已显示出比“先检测再计数”方法[22、19、62、12]更为鲁棒，因为前者对遮挡不敏感并且不需要在早期就进行二元化决策。

密度图估计方法发展中的关键步骤是训练从输入图像映射到相应的带注释的密度图的深度神经网络。在所有现有的人群计数数据集[15、60、14、51]中，每个训练图像的带注释的密度图是一个稀疏的二进制掩膜（binary mask），其中每个人的头或前额都用一个点标记。由于描述空间范围所需的费力工作，尤其是当遮挡模糊太大时，没有提供每个人的空间范围。给定带有点注释的训练图像，训练密度图估计网络等效于优化网络参数，以最小化可预测损失密度的可微损失函数，该函数可测量预测密度图和点注释图之间的差异。值得注意的是，前者是一个密集的实值矩阵，而后者是一个稀疏的二进制矩阵。给定点的稀疏性，很难训练基于带注释的密度图和预测的密度图之间的像素级差异定义的函数，因为重建损失在稀疏二进制矩阵中的0和1之间非常不平衡。缓解此问题的一种方法是将每个带注释的点变成高斯块（Gaussian blob），以便GT更加平衡，因此网络更易于训练。几乎所有先前的人群密度图估计方法[56、57、60、38、20、33、35、4、28、50、27、40、29、26]都遵循了这一约定。不幸的是，所得网络的性能高度依赖于此“伪GT（pseudo ground truth）”的质量，但是鉴于拥挤的场景的透视图中人的大小和形状的巨大差异，为高斯块（Gaussian blobs）设置正确的宽度并非易事。

最近，Ma等 [31]提出了贝叶斯损失来测量预测密度图和注释密度图之间的差异。该方法将二进制GT注释图转换为N个“平滑GT”密度图，其中N是人数。给定该像素的位置，平滑的GT密度图的每个像素值就是相应注释点的后验概率。从经验上看，该方法的性能优于其他前述方法[60、38、20、33、35、4]。但是，此损失函数存在两个主要问题。首先，它还需要高斯核来为每个带注释的点构造似然函数，这涉及设置核宽度（kernel width）。其次，这种损失对应于一个不确定的方程组，具有无限多个解。对于许多与GT密度图不相似的密度图，损失可能为0。结果，使用此损失进行训练可能会导致预测的密度图与GT密度图非常不同。

在本文中，我们通过以下贡献解决了现有方法的缺陷。
• 我们在理论上和经验上表明，将高斯方法强加于注释会损害人群计数网络的泛化性能。
• 我们建议使用DM-Count，这是一种针对人群计数d分布匹配的方法。与以前的工作不同，DM-Count不需要任何高斯平滑GT注释。相反，我们使用最优传输（OT）来测量归一化的预测密度图和归一化的GT密度图之间的相似度。为了稳定OT计算，我们进一步添加了总变化（TV）损失。
• 我们在我们的方法中给出了计数损失（counting loss），OT损失，TV损失和总体损失（overall loss）的泛化误差范围。所有边界都比高斯平滑方法的边界更严格。
• 根据经验，我们的方法在四个具有挑战性的人群计数数据集：UCF-QNRF，NWPU，ShanghaiTech和UCF-CC50上大大改进了现有技术。值得注意的是，我们的方法将NWPU数据集上已发布的最新MAE降低了约16％。

二. 先前的工作

2.1 人群计数方法

人群计数方法可分为三类：检测然后计数方法，直接回归法计数和密度图估计法。早期方法[22、19、62、12]可以检测图像中的人，头部或上半身。但是，对于人群密集的人群来说，准确检测是困难的。此外，它还需要边界框注释，由于严重的遮挡，这是一个费力且模棱两可的过程。后来的方法[5、6、49、7]避免了检测问题，并直接学习从特征向量中对计数进行回归。但是它们的结果难以解释，并且点注释图的利用不足。最新研究[20、35、15、4、31、50、27、40、29、26、54、8、25、55、61、59、17、48、21、23、30、47、53 43、37、56、18、39、24、44、42]是基于密度图估计的，它已显示出是比先检测再计数和计数回归方法更可靠的方法。
密度图估计方法通常基于高斯平滑密度图和预测密度图之间的像素差异来定义训练损失。而不是使用单个内核宽度来平滑点注释，[60，14，47]使用自适应内核宽度。根据到注释点的最近邻居的距离来选择内核宽度。具体来说，[15]在不同的密度水平上生成了多个平滑的GT密度图。最终损失合并了来自多个密度级别的重建误差（reconstruction errors）。但是，这些方法假定人群均匀分布。实际上人群分布是非常不规则的。贝叶斯损失方法[31]使用高斯为每个带注释的点构造似然函数。但是，由于损失未确定，因此可能无法预测正确的密度。详细分析可以在第4.2节中找到。

2.2 最优传输

我们提出了一种基于最优运输（OT）的新颖损失函数[46]。 为了更好地理解所建议的方法，我们在本节中简要回顾一下Monge-Kantarovich OT公式。

最优运输是指将一种概率分布转换为另一种概率分布的最优成本。令$\mathcal{X}={\left\{{\mathbf{x}}_i\mid {\mathbf{x}}_i\in {\mathbb{R}}^d\right\}}_{i=1}^n$ 和$\mathcal{Y}={\left\{{\mathbf{y}}_j\mid {\mathbf{y}}_j\in {\mathbb{R}}^d\right\}}_{j=1}^n$ 为两个$d$ 维向量空间的点集。令$\mu$ 和$\nu$ 为两个定义在 $\mathcal{X}$ 和$\mathcal{Y}$ 上的概率测度，其中，$\mu ,\nu \in {\mathbb{R}}_{+}^n$ 且 $1_n^T\mathbf{\mu }=1_n^T\mathbf{\nu }=1(1_n$ 是一个 $n$ 维全 1 向量 ）。 令 $c:\mathcal{X}\times \mathcal{Y}\mapsto {\mathbb{R}}_{+}$ 为从点 $\mathcal{X}$ 移动到点 $\mathcal{Y}$ 的成本函数， $\mathrm{C}$ 为两个点集之间对应的 $n\times n$ 成本矩阵：${\mathbf{C}}_{ij}=c\left({\mathbf{x}}_i,{\mathbf{y}}_j\right)$ . 令$\Gamma$ 为将概率质量从 $\mathcal{X}$ 传递到 $\mathcal{Y}$ 的所有可能方式的集合: $\Gamma =\left\{\gamma \in {\mathbb{R}}_{+}^{n\times n}:\gamma 1=\mathbf{\mu },{\gamma }^{T}1=\mathbf{\nu }\right\}$ 。介于 $\mu$ 和 $\nu$ 之间的Monge-Kantorovich的最优传输（OT）成本定义为：
$$\mathcal{W}(\mathbf{\mu },\mathbf{\nu })=\underset{\gamma \in \Gamma }{\min }⟨\mathbf{C},\gamma ⟩$$
Intuitively, if the probability distribution $\mu$ is viewed as a unit amount of “dirt” piled on $\mathcal{X}$ and $\mu$ a unit amount of dirt piled on $\mathcal{Y}$, the OT cost is the minimum “cost” of turning one pile into the other. The OT cost is a principal measurement to quantify the dissimilarity between two probability distributions, also taking into account the distance between “dirt” locations.(这一段不知道怎么翻译。。。)
OT成本也可以通过对偶公式（2）计算：
$$\mathcal{W}(\mathbf{\mu },\mathbf{\nu })=\underset{\mathbf{\alpha },\mathbf{\beta }\in {\mathbb{R}}^n}{\max }⟨\mathbf{\alpha },\mathbf{\mu }⟩+⟨\mathbf{\beta },\mathbf{\nu }⟩,\text{ s.t. }{\alpha }_i+{\beta }_j\le c\left({\mathbf{x}}_i,{\mathbf{y}}_j\right),\forall i,j$$

三. DM-Count：用于人群计数的分布匹配

我们认为人群计数是分布匹配问题。 在本节中，我们提出DM-Count：用于人群计数的分布匹配，输入一张图像并输出密度值图的人群计数的网络。通过对预测密度图求和来获得最终计数估计。 DM-Count与不同的网络体系结构无关。 在我们的实验中，我们使用与贝叶斯损失论文相同的网络[31]。 与所有以前需要使用高斯来平滑GT情况注释的密度图估计方法不同，DM-Count不需要任何高斯来预处理GT注释。

令$\mathbf{z}\in {\mathbb{R}}_{+}^n$ 表示点注释的矢量化二进制映射，而$\hat{\mathbf{z}}\in {\mathbb{R}}_{+}^n$ 由神经网络返回的矢量化预测密度图。 通过将$\mathrm{z}$ 和 $\hat{\mathrm{z}}$ 视为未归一化的密度函数，我们使用以下三项来表示DM-Count中的损失函数：计数损失，OT损失和总变化（TV）损失。 第一项测量总质量之间的差异，而后两项测量归一化密度函数分布之间的差异。

计数损失。 令 $\Vert \cdot {\Vert }_1$ 表示向量的 $L_1$ 范数，因此$\Vert \mathbf{z}{\Vert }_1，\Vert \hat{\mathbf{z}}{\Vert }_1$ 分别是基本事实和预测计数。 人群计数的目标是使$\Vert \hat{\mathbf{z}}{\Vert }_1$ 尽可能接近 $\Vert \mathbf{z}{\Vert }_1$ ，然后 计数损失定义为它们之间的绝对值之差：
$${\ell }_C(\mathbf{z},\hat{\mathbf{z}})=\left|\Vert \mathbf{z}{\Vert }_1-\Vert \hat{\mathbf{z}}{\Vert }_1\right|$$
最优传输损失。 $\mathbf{z}$ 和 $\hat{\mathbf{z}}$ 都是非归一化的密度函数，但是我们可以通过将它们除以它们各自的总和来将它们转换为概率密度函数（pdfs）。 除了OT，Kullback-Leibler散度和Jensen-Shannon散度也可以测量两个pdf之间的相似性。 但是，如果源分布与目标分布不重叠，这些测量将不会提供有效的梯度来训练网络[32]。 因此，我们建议在这项工作中使用OT。 我们将OT损失定义如下：
$${\ell }_{OT}(\mathbf{z},\hat{\mathbf{z}})=\mathcal{W}\left(\frac{\mathbf{z}}{\Vert \mathbf{z}{\Vert }_1},\frac{\hat{\mathbf{z}}}{\Vert \hat{\mathbf{z}}{\Vert }_1}\right)=⟨{\mathbf{\alpha }}^{\ast },\frac{\mathbf{z}}{\Vert \mathbf{z}{\Vert }_1}⟩+⟨{\mathbf{\beta }}^{\ast },\frac{\hat{\mathbf{z}}}{\Vert \hat{\mathbf{z}}{\Vert }_1}⟩$$
其中${\alpha }^{\ast }$ 和${\beta }^{\ast }$ 是公式$（2）$ 的解。我们使用二次传输成本，即 $c(\mathbf{z}(i),\hat{\mathbf{z}}(j))=\Vert \mathbf{z}(i)-\hat{\mathbf{z}}(j){\Vert }_2^2,$ 其中 $\mathbf{z}(i)$ 和$\hat{\mathbf{z}}(j)$ 分别是位置 $i$ 和 $j$ 的$2\mathrm{D}$ 坐标。为了防止除以零的错误，我们在分母中增加了机器精度数。 由于$\hat{z}$ 中的元素为非负数，方程（4）关于$\hat{z}$ 的梯度为：
$$\frac{\partial {\ell }_{OT}(\mathbf{z},\hat{\mathbf{z}})}{\partial \hat{\mathbf{z}}}=\frac{{\mathbf{\beta }}^{\ast }}{\Vert \hat{\mathbf{z}}{\Vert }_1}-\frac{⟨{\mathbf{\beta }}^{\ast },\hat{\mathbf{z}}⟩}{\Vert \hat{\mathbf{z}}{\Vert }_1^2}$$
可以通过反向传播此梯度，以了解密度估计网络的参数。

总变化损失。 在每个训练迭代中，我们使用Sinkhorn算法[34]来近似${\alpha }^{\ast }$ 和 ${\beta }^{\ast }$ 。时间复杂度为$O\left(n^2\log n/{ϵ}^2\right)$ [9]，其中 $ϵ$ 是所需的最优间隔，即返回的目标与最佳目标之间的差异。当使用Sinkhorn算法进行优化时，目标函数在开始时急剧下降，但在以后的迭代中仅缓慢收敛到最优解。在实践中，我们设置最大迭代次数，而Sinkhorn算法仅返回近似解。结果，当我们使用Sinkhorn算法优化OT损失时，预测的密度图最终接近GT密度图，但并不完全相同。 OT损失将很好地逼近人群的密集区域，但是对于人群的低密度区域，近似值可能会更差。为了解决这个问题，我们另外使用总变化（TV）损失，定义为 ：
$${\ell }_{TV}(\mathbf{z},\hat{\mathbf{z}})={\Vert \frac{\mathbf{z}}{\Vert \mathbf{z}{\Vert }_1}-\frac{\hat{\mathbf{z}}}{\Vert \hat{\mathbf{z}}{\Vert }_1}\Vert }_{TV}=\frac{1}{2}{\Vert \frac{\mathbf{z}}{\Vert \mathbf{z}{\Vert }_1}-\frac{\hat{\mathbf{z}}}{\Vert \hat{\mathbf{z}}{\Vert }_1}\Vert }_1$$
TV损失也将增加训练过程的稳定性。 用Sinkhorn算法优化OT损失是最小-最大鞍点的优化过程，类似于GAN优化[13]。 如Pix2Pix GAN [16]所示，可以通过增加重建损失来增加GAN训练的稳定性。 为此，TV损失类似于重建损失，并且还增加了训练过程的稳定性。TV损失对预测密度图 $\hat{\mathbf{z}}$ 的梯度为：
$$\frac{\partial {\ell }_{TV}(\mathbf{z},\hat{\mathbf{z}})}{\partial \hat{\mathbf{z}}}=-\frac{1}{2}\left(\frac{\mathrm{sign}(\mathbf{v})}{\Vert \hat{\mathbf{z}}{\Vert }_1}-\frac{⟨\mathrm{sign}(\mathbf{v}),\hat{\mathbf{z}}⟩}{\Vert \hat{\mathbf{z}}{\Vert }_1^2}\right)$$
其中，$\mathbf{v}=\mathbf{z}/\Vert \mathbf{z}{\Vert }_1-\hat{\mathbf{z}}/\Vert \hat{\mathbf{z}}{\Vert }_1,$ ，$\mathrm{sign}(\cdot )$ 是向量每个元素上的符号函数。
总体损失函数（The Overall Objective）。 总体损失函数是计数损失，OT损失和TV损失的和：
$$\ell (\mathbf{z},\hat{\mathbf{z}})={\ell }_C(\mathbf{z},\hat{\mathbf{z}})+{\lambda }_1{\ell }_{OT}(\mathbf{z},\hat{\mathbf{z}})+{\lambda }_2\Vert \mathbf{z}{\Vert }_1{\ell }_{TV}(\mathbf{z},\hat{\mathbf{z}})$$

其中 ${\lambda }_1$ 和 ${\lambda }_2$ 是OT和TV损失的可调超参数。 为确保TV损失与计数损失具有相同的比例，我们将此损失项与总人数相乘。

给定 $K$ 训练图像 ${\left\{I_k\right\}}_{k=1}^K$ 及其相应的点注释图 ${\left\{{\mathbf{z}}_k\right\}}_{k=1}^K$ ，我们将通过最小化 $L(f)=\frac{1}{K}{\sum }_{k=1}^{\bar{K}}\ell \left({\mathbf{z}}_k,f\left(I_k\right)\right)$ 来学习用于密度图估计的深度神经网络 $f$ 。

四. 泛化边界和理论分析

在本节中，我们分析了高斯平滑方法，贝叶斯损失和提出的DM-Count的理论特性。 本节中定理的证明可以在补充材料中找到。 首先，我们在下面介绍一些符号。

令 $\mathcal{D}=\{(I,\mathbf{z})\}$ 是人群图像和相应点注释图的联合分布。令 $\mathcal{H}$ 为假设空间。每个 $h\in \mathcal{H}$ 把$I\in \mathcal{I}$ 映射到 $\mathbf{z}\in \mathcal{Z}$ 的每个维度。令 $\mathcal{F}=\mathcal{H}\times \cdots \times \mathcal{H}(n\text{ times})x$ 为映射空间。每个 $f\in \mathcal{F}$ 把 $I\in \mathcal{I}$ 映射到 $\mathbf{z}\in \mathcal{Z}$ 。假设 $\mathrm{t}$ 为每个 $\mathbf{z}\in \mathcal{D}$ 中的高斯平滑密度图，并令 $\tilde{\mathcal{D}}=\{(I,\mathbf{t})\}$ 为 $(I,\mathbf{t})$ 的联合分布。让 $S={\left\{\left(I_k,{\mathbf{z}}_k\right)\right\}}_{k=1}^K$ 和 $\tilde{S}={\left\{\left(I_k,{\mathbf{t}}_k\right)\right\}}_{k=1}^K$ 为含有 $K$ 个样本的有限集，且分别为从 $\mathcal{D}$ 和 $\tilde{\mathcal{D}}$ 中采样的独立同分布样本。假设 $R_S(\mathcal{H})$ 表示 $\mathcal{H}$ 关于 $S$ 的经验拉德马赫尔复杂度(empirical Rademacher complexity)[3]。给定数据集 $D\in \{\mathcal{D},S,\tilde{\mathcal{D}},\tilde{S}\}$, 映射 $f\in \mathcal{F}$ 和损失函数 $\ell$ , 令 $\mathcal{R}(D,f,\ell )={\mathbb{E}}_{(I，\mathbf{s})\sim D}[\ell (\mathbf{s},f(I))]$ 表示预期风险。令 ${\ell }_1(\mathbf{z},\hat{\mathbf{z}})=\Vert \mathbf{z}-\hat{\mathbf{z}}{\Vert }_1$ 。设 $f_{\Delta }^D={\mathrm{argmin}}_{f\in \mathcal{F}}\mathcal{R}\left(D,f,{\ell }_{\Delta }\right)$ 为损失 ${\ell }_{\Delta }$ 在数据集 $D$ 上的极小值$\mathcal{R}\left(D,f,{\ell }_{\Delta }\right)$，其中 $D\in \{\mathcal{D},S,\tilde{\mathcal{D}},\tilde{S}\}$ ， $\Delta \in \{1,C,OT,TV,\varnothing \}$ 。

4.1 高斯平滑方法的广义误差界

许多现有方法（例如[60、20、35]）都使用高斯平滑的注释图进行训练。下面给出了在密度图上使用 ${\ell }_1$ 损失的泛化误差界。
定理1 ：假设 $\forall f\in \mathcal{F}$ 且 $(I,\mathbf{t})\sim \tilde{\mathcal{D}}$,有 $\ell (\mathbf{t},f(I))\le B.$ 那么, 对任意 $0<\delta <1$, 至少以概率 $1-\delta$ 有,
a) 泛化误差的上边界为：
$$\mathcal{R}\left(\mathcal{D},f_1^{\tilde{S}},{\ell }_1\right)\le \mathcal{R}\left(\tilde{\mathcal{D}},f_1^{\tilde{\mathcal{D}}},{\ell }_1\right)+2n{R}_S(\mathcal{H})+5B\sqrt{2\log (8/\delta )/K}+{\mathbb{E}}_{(I,\mathbf{z})\sim \mathcal{D}}\Vert \mathbf{z}-\mathbf{t}{\Vert }_1$$
b) 泛化误差的下边界为：
$$\mathcal{R}\left(\mathcal{D},f_1^{\tilde{S}},{\ell }_1\right)\ge \left|{\mathbb{E}}_{(I,\mathbf{z})\sim \mathcal{D}}\Vert \mathbf{z}-\mathbf{t}{\Vert }_1-\mathcal{R}\left(\tilde{\mathcal{D}},f_1^{\tilde{S}},{\ell }_1\right)\right|$$
在这个定理中,随着样本数 $K$ 区域无穷, $2n{R}_S(\mathcal{H})$ 和 $5B\sqrt{2\log (8/\delta )/K}$ 降为 $0$ 。定理 $1.a$ ) 表明期望风险$\mathcal{R}\left(\mathcal{D},f_1^{\tilde{S}},{\ell }_1\right)$ 的上边界（最差情况） ，这个边界是使用在高斯平滑GT上训练的经验极小值对真实GT数据进行评估的。在足够训练数据条件下不超过 $\mathcal{R}\left(\tilde{\mathcal{D}},f_1^{\tilde{\mathcal{D}}},{\ell }_1\right)+{\mathbb{E}}_{(I,\mathbf{z})\sim \mathcal{D}}\Vert \mathbf{z}-\mathbf{t}{\Vert }_1$ 定理 $1.b$ ) 表明期望风险$\mathcal{R}\left(\mathcal{D},f_1^{\tilde{S}},{\ell }_1\right)$ 的下边界（最好情况）不小于 $\left|{\mathbb{E}}_{(I,\mathbf{z})\sim \mathcal{D}}\Vert \mathbf{z}-\mathbf{t}{\Vert }_1-\mathcal{R}\left(\tilde{\mathcal{D}},f_1^{\tilde{S}},{\ell }_1\right)\right|.$ 这意味着$\mathcal{R}\left(\tilde{\mathcal{D}},f_1^{\tilde{S}},{\ell }_1\right)\le {\mathbb{E}}_{(I,\mathbf{z})\sim \mathcal{D}}\Vert \mathbf{z}-\mathbf{t}{\Vert }_1,$ 于是最小的是 $\mathcal{R}\left(\tilde{\mathcal{D}},f_1^{\tilde{S}},{\ell }_1\right)$，最大的期望风险是 $\mathcal{R}\left(\mathcal{D},f_1^{\tilde{S}},{\ell }_1\right)$. 换句话说,模型 $f_1^{\tilde{S}}$ 在高斯平滑的GT $\tilde{\mathcal{D}}$ 上表现越好, 在实际GT $\mathcal{D}$ 上的泛化性能越差. 此外, 由于 $\mathcal{R}\left(\tilde{\mathcal{D}},f_1^{\tilde{S}},{\ell }_1\right)\ne {\mathbb{E}}_{(I,\mathbf{z})\sim \mathcal{D}}\Vert \mathbf{z}-\mathbf{t}{\Vert }_1,$ 当$\mathcal{R}\left(\tilde{\mathcal{D}},f_1^{\tilde{S}},{\ell }_1\right)=0.$，有 $\mathcal{R}\left(\mathcal{D},f_1^{\tilde{S}},{\ell }_1\right)>0.\mathcal{R}\left(\mathcal{D},f_1^{\tilde{S}},{\ell }_1\right)$ 最大能够到 ${\mathbb{E}}_{(I,\mathbf{z})\sim \mathcal{D}}\Vert \mathbf{z}-\mathbf{t}{\Vert }_1$。这并非我们想要的，因为我们希望在真实GT上评估的风险 $\mathcal{R}\left(\mathcal{D},f_1^{\tilde{S}},{\ell }_1\right)$ 尽可能趋于 $0$。

4.2 不确定的贝叶斯损失

贝叶斯损失[31]为：

$${\ell }_{\text{Bayesian}}(\mathbf{z},\hat{\mathbf{z}})=\sum _{i=1}^N\left|1-⟨{\mathbf{p}}_i,\hat{\mathbf{z}}⟩\right|,\text{ where }{\mathbf{p}}_i=\frac{\mathcal{N}\left({\mathbf{q}}_i,{\sigma }^2{1}_{2\times 2}\right)}{{\sum }_{i=1}^N\mathcal{N}\left({\mathbf{q}}_i,{\sigma }^2{1}_{2\times 2}\right)}$$
其中 $N$ 是 $\mathbf{z}的人头数,$ $\mathcal{N}\left({\mathbf{q}}_i,{\sigma }^2{1}_{2\times 2}\right)$ 是以 ${\mathbf{q}}_i$ 为均值，方差为 ${\sigma }^2{1}_{2\times 2}$ 的高斯分布。 ${\mathbf{q}}_i$ 是 $\mathbf{z}$ 中的第 $i^{th}$ 个标注点。. ${\mathbf{p}}_i$ 和 $\mathbf{z}$ 的维度为 $n,$ 即密度图的像素点数。 但是，由于标注的点数 $N$小于 $n,$贝叶斯损失是不确定的。 对于GT标注 $\mathbf{z}$, 有无穷多个 $\hat{\mathbf{z}}$ 满足 ${\ell }_{\text{Bayesian}}(\mathbf{z},\hat{\mathbf{z}})=0$ 且 $\hat{\mathbf{z}}\ne \mathbf{z}.$ 因此，预测的密度图可能与GT密度图有很大不同。

4.3 DM-Count 中的损失函数的泛化误差界

在下面的定理中，我们给出了所提出方法的损失函数的泛化误差界。
定理 2 ： 假设 $\forall f\in \mathcal{F}$ 且 $(I,\mathbf{z})\sim \mathcal{D}$,有 $\Vert \mathbf{z}{\Vert }_1\ge 1,\Vert f(I){\Vert }_1\ge 1$ (可以通过向 $\mathrm{z}$ 和 $f(I)$ 都添加值为1的虚拟维来满足) 且 ${\ell }_C(\mathrm{z},f(I))\le B.$ 那么, 对任意 $0<\delta <1$, 至少以概率 $1-\delta$ 有：
$a.)$ 计数损失的泛化误差界为:
$$\mathcal{R}\left(\mathcal{D},f_C^S,{\ell }_C\right)\le \mathcal{R}\left(\mathcal{D},f_C^{\mathcal{D}},{\ell }_C\right)+2n{R}_S(\mathcal{H})+5B\sqrt{2\log (8/\delta )/K}$$
$b.)$ OT损失的泛化误差界为:
$$\mathcal{R}\left(\mathcal{D},f_{OT}^S,{\ell }_{OT}\right)\le \mathcal{R}\left(\mathcal{D},f_{OT}^{\mathcal{D}},{\ell }_{OT}\right)+4{\mathbf{C}}_{\infty }{n}^2{R}_S(\mathcal{H})+5{\mathbf{C}}_{\infty }\sqrt{2\log (8/\delta )/K}$$
$c.)$ TV损失的泛化误差界为:
$$\mathcal{R}\left(\mathcal{D},f_{TV}^S,{\ell }_{TV}\right)\le \mathcal{R}\left(\mathcal{D},f_{TV}^{\mathcal{D}},{\ell }_{TV}\right)+n^2{R}_S(\mathcal{H})+5\sqrt{2\log (8/\delta )K}$$
$d.)$ 总体损失的泛化误差界为:
$$\begin{array}{r}\mathcal{R}\left(\mathcal{D},f^S,\ell \right)\le \mathcal{R}\left(\mathcal{D},f^{\mathcal{D}},\ell \right)+\left(2n+4{\lambda }_1{\mathbf{C}}_{\infty }{n}^2+{\lambda }_{2}N{n}^2\right)R_S(\mathcal{H})\\ +5\left(B+{\lambda }_1{\mathbf{C}}_{\infty }+{\lambda }_{2}N\right)\sqrt{2\log (8/\delta )K}\end{array}$$
其中，${\mathbf{C}}_{\infty }$ 是OT成本矩阵的最大值，$N=\sup \left\{\Vert \mathbf{z}{\Vert }_1\mid \forall (I,\mathbf{z})\sim \mathcal{D}\right\}$ 为数据集上最大的人头数。
在上面的理论中，随着 $K$ 增加，$R_S(\mathcal{H})$ 和 $\sqrt{2\log (1/\delta )K}$ 减小。 所有使用经验最小化器（empirical minimizers） $f_{\Delta }^{\dot{S}}$ 的期望风险 $\mathcal{R}\left(\mathcal{D},f_{\Delta }^S,{\ell }_{\Delta }\right)$ 收敛到使用最优最小化器（optimal minimizers） $f_{\Delta }^{\mathcal{D}}$ 的期望风险 $\mathcal{R}\left(\mathcal{D},f_{\Delta }^{\mathcal{D}},{\ell }_{\Delta }\right)$ ， $\Delta \in \{C,OT,TV,\varnothing \}$ 。这意味着所有上限都很严格。 此外，所有上限都比定理$1.\mathrm{a}$ ) 中所示的高斯平滑方法的上限更严格。定理$2.\mathrm{b}$ ) 中OT损失的界限与最大传输成本 ${\mathrm{C}}_{\infty }$ 有关。因此，我们需要在OT中使用较小的传输成本以获得更好的泛化性能。$R_S(\mathcal{H})$ 的计数损耗系数为 $O(n)$，OT损耗和TV损耗的系数为 $O\left(n^2\right)$ 。 这意味着对于更大的图像尺寸，我们需要更多的图像进行训练。 当使用计数损失时，该数字与 $\mathbf{z}$ 的大小呈线性关系，而使用OT损失或TV损失时，则为平方关系。 当使用这三个损失函数时，我们需要将 ${\lambda }_1$ 和 ${\lambda }_2$ 设置为较小，以便平衡这三个损失值。

五. 实验

在本节中，我们将介绍有关在toy data和基准人群计数数据集（benchmark crowd counting datasets）上的实验。 在补充材料中可以找到更详细的数据集描述，实现细节和实验设置。

5.1 Toy Data 数据集上的结果

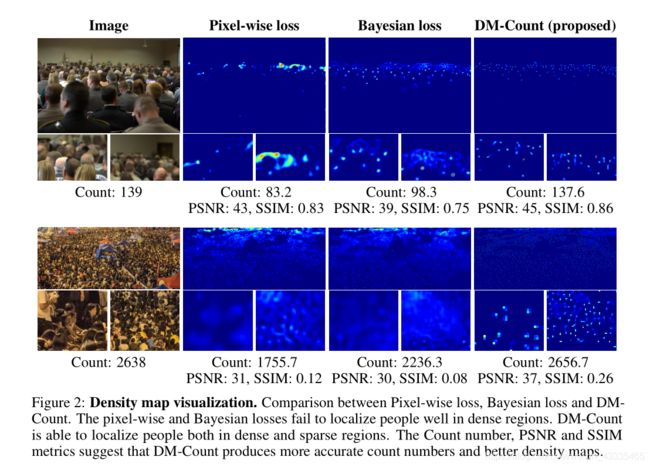
为了理解不同方法的经验行为，我们考虑一个 toy problem，其中的任务是使用像素级损失，贝叶斯损失和DM-Count将源密度图 $\hat{\mathbf{z}}$ 移动到目标密度图 $\mathbf{z}$ 。源密度图 $\hat{\mathbf{z}}$ 是从 $0$ 到 $0.01$ 之间的均匀分布初始化的，目标密度图显示在图1的最左侧。所有三种方法都从相同的源密度图开始。图1为最终收敛时 $\hat{\mathbf{z}}$ 的可视化图。逐像素损失会产生具有更高计数的模糊密度图。在计数误差、峰值信噪比（PSNR）和图像中的结构相似性（SSIM）[52]方面，贝叶斯损耗的性能要好于像素级损耗[52]，但最终的密度图与目标值有很大不同，在没有注释点的许多位置具有较高的值。这证实了我们的分析，即贝叶斯损失对应于一个不确定系统，因此输出密度图可能与目标密度图有很大差异。相比之下，DM-Count能够产生更准确的计数和密度图。 DM-Count在PSNR和SSIM方面都大大优于贝叶斯损失。

5.2 Benchmark 数据集上的结果

我们在四个具有挑战性的人群计数数据集上进行实验：UCF-QNRF [15]，NWPU [51]，ShanghaiTech [60]和UCF-CC-50 [14]。值得注意的是，NWPU数据集是当今公开可用的规模最大，最具挑战性的人群计数数据集。测试图像的GT计数不会发布，并且必须通过提交给评估服务器https://www.crowdbenchmark.com/nwpucrowd.html 来获得测试集上的结果。在先前的工作[35、15、4、14、60]之前，我们使用以下度量：平均绝对误差（MAE），均方根误差（RMSE）和平均归一化绝对误差（NAE）作为评估指标。对于所有三个指标，越小越好。为了进行公平的比较，我们使用与贝叶斯损失论文[31]中相同的网络。在所有实验中，我们将${\lambda }_1=0.1，{\lambda }_2=0.01$，并将Sinkhorn熵正则化参数设置为10。Sinkhorn迭代次数设置为100。平均而言，每个图像的OT计算时间为25ms。

定量结果。 表1和表2比较了DM-Count与各种方法的性能。在所有实验中，除了CAN方法，DM-Count 在MSE性能上优于其他所有方法（基于可比的NWPU数据集）。尽管我们在所有实验中对DM-Count使用相同的超参数集，但DM-Count仍可达到最佳性能，这表明DM-Count的性能在各种数据集中稳定。

在所有实验中，DM-Count在与DM-Count相同的网络体系结构和训练过程中时，其性能优于逐像素（Pixel-wise）损失和贝叶斯损失。这证明了我们提出的损失函数的有效性。逐像素（Pixel-wise）损失比表1中的DM-Count严重得多。此外，即使未使用[4，47]中的多尺度体系结构或[2，50]中的更深层网络，DM-Count仍然在所有四个数据集上均达到最先进的性能。这表明在人群计数中具有良好的损失函数非常重要。

在UCF-QNRF和NWPU的大型且具有挑战性的数据集上，DM-Count明显优于最新方法。具体来说，在UCF-QNRF数据集上，DM-Count将贝叶斯损失的MAE和MSE分别从88.7降低到85.6和从154.8降低到148.3。值得注意的是，在NWPU测试集上（通过提交给评估服务器获得），DM-Count大大降低了MAE和NAE，MAE从105.4降低到88.4，NAE从0.203降低到0.169。

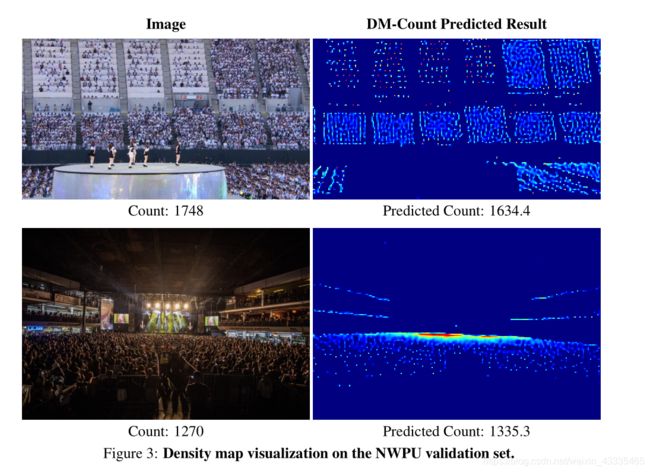
定性结果。 图2显示了像素级损失，贝叶斯损失和DM-Count的预测密度图。该图表明：1）DM-Count产生的计数值更接近于GT实际值，2）DM-Count产生的密度图比逐像素损失和贝叶斯损失更清晰。在图2中，DM-Count产生的PSNR和SSIM比逐像素和贝叶斯损耗高得多。在整个UCF-QNRF测试集上，逐像素损失的平均PSNR和SSIM分别为34.79和0.43，贝叶斯损失为34.55和0.42，DM计数为40.65和0.55。由于逐像素损失使用了高斯平滑的地面实况，因此它产生的密度比实际地面实况更模糊。这从经验上验证了我们对高斯平滑方法的广义界限的理论分析。如图所示，Pixelwise和贝叶斯损失无法将人定位在人口稠密的地区。相反，DM-Count在人口稠密和稀疏地区都能很好地定位人们。图3示出了通过DM计数的预测密度图。预测的密度图与稀疏和稠密地区的人群密度非常吻合，证明了DM-Count在空间密度估计中的有效性。

5.3 模型简化测试

超参数研究。 我们在UCF-QNRF数据集的DM-Count中调整 $\lambda 1$ 和 $\lambda 2$ 。 首先，我们将 ${\lambda }_1$ 固定为0.1，并将 ${\lambda }_2$ 从0.01、0.05调整为0.1。 MAE从85.6、87.8到88.5不等。 由于${\lambda }_2=0.01$ 可获得最佳结果，我们将 ${\lambda }_2$ 固定为0.01，并将 ${\lambda }_1$ 从0.01、0.05调整为0.1。 MAE从87.2、86.2到85.6不等。 因此，我们设置 ${\lambda }_1=0.1，{\lambda }_2=0.01$ 并将其用于所有数据集。

Sinkhorn迭代次数的影响。 表3列出了使用不同数量的Sinkhorn迭代的UCF、QNRF数据集上DM-Count的结果。 如下表所示，使用少量迭代会降低DM-Count的性能，这表明我们获得的OT解决方案不准确。 当迭代次数增加到100时，DM-Count的性能将超过以前的最新水平。 迭代次数超过100后性能稳定下来。因此，在我们所有的实验中，我们对DM-Count使用100个Sinkhorn迭代。

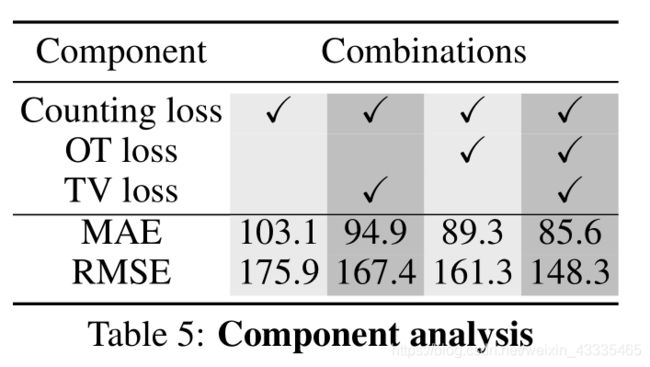
每个损失函数的贡献。 DM-Count 计数损失函数由三个部分组成，计数损失，OT损失和TV损失。我们研究了在UCF-QNRF数据集上每个函数的贡献。 结果列在表5中。如表中所示，所有组分对于最终性能都是必不可少的。 但是，OT损失是最重要的组成部分。

对有噪声的注释的鲁棒性。 人群注释是通过在人身上放置一个点。 这样的过程是模棱两可的，并且可能导致不可避免的注释错误。 我们研究了不同的损失函数对于注释错误的表现。 我们向原始注解添加统一的随机噪声，并使用相同的噪声注解训练不同的模型。 噪声是在图像高度的0％到5％之间随机产生的，平均约为80个像素。 如表4所示，与逐像素贝叶斯损失相比，提出的DM-Count对注释错误更具有鲁棒性。

六. 结论

在本文中，我们已经表明，使用高斯核对GT点注释进行平滑处理会损害模型在真实的GT数据上进行测试的泛化范围。 相反，我们将人群计数视为分布匹配问题，并提出基于优化传输的DM-Count来解决此问题。 与先前的工作不同，DM-Count不需要高斯核来平滑带注释的点。 DM-Count的泛化误差范围比高斯平滑方法的泛化误差范围更严格。 在四个人群计数基准上进行的大量实验表明，DM-Count明显优于以前的最新方法。