详解GPU显存和batch size的关系
最近在训练模型的时候突然被问到如下几个看似简单,实则一点也不难的问题
- 在显存充足的情况下增加 batch size 大小会加快训练吗?
- 扩大 batch size 占用的显存是如何变化的,显存是线性增加吗?
- 扩大 batch size 后是哪些因素导致了显存占用增加?
前两个问题有过训练模型经验的都知道增加batch size并不会一直能加快训练,而扩大batch size也和显存占用不成线性关系。而对第三个问题被问到的一瞬间确实没有反应过来,因此便有了这篇文章。本文将对以上三个问题进行详细分析
文章目录
- 1. GPU 基础
-
- 1.1 显存
- 1.2 算力
- 1.3 带宽
- 2. 神经网络显存占用
-
- 2.1 模型参数
- 2.2 模型的输入输出
- 2.3 优化器和梯度
- 3. 计算量
- 4. 结论
1. GPU 基础
1.1 显存
此处不多说,就是GPU的内存,越大越好,下面展示一些GPU的显存大小
| GPU型号 | 显存大小 |
|---|---|
| 1060 | 6G |
| 1080 | 8G |
| T4 | 16G |
| V100 | 32G |
| A100 | 80G |
显存分析
在深度学习中常用的数值类型是float32,一个字节8位,float32数值类型占用4个字节。如果现在有一个1000x1000的矩阵,存储类型为float32,那么占用的显存差不多就是
1000 × 1000 × 4 = 4 × 1 0 6 B ≈ 4000 K B ≈ 4 M B 1000 \times 1000 \times 4 = 4 \times 10^6 B \approx 4000KB \approx 4MB 1000×1000×4=4×106B≈4000KB≈4MB
注意此处为了计算方便使用了1000进制,实际上为1024
前面介绍的 Stable Diffusion XL 的Unet参数量为2.6B(26亿),那么其占用显存计算如下(假设按 float32 存储):
26 × 1 0 8 × 4 = 104 × 1 0 8 B ≈ 10.4 G B 26\times 10^8 \times 4 = 104 \times 10^8 B \approx 10.4 GB 26×108×4=104×108B≈10.4GB
1.2 算力
GPU计算单元类似于CPU中的核,用来进行数值计算。衡量计算量的单位是flop: the number of floating-point multiplication-adds,即浮点数先乘后加算一个flop。
1*2+3 1 flop
1*2 + 3*4 + 4*5 3 flop
算力用于衡量GPU的计算能力,计算能力越强大,速度越快。衡量计算能力的单位是flops,即每秒能执行的flop数量。
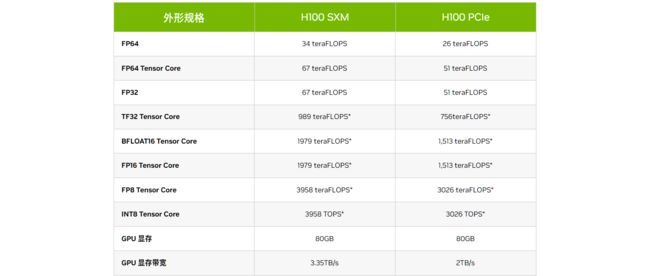
下图展示了V100的算力,其中TFLOPS是teraFLOPS的缩写,等于每秒一万亿( 1 0 12 10^{12} 1012) 次的浮点运算。常见的单位还有PFLOPS(petaFLOPS)等于每秒一千万亿( 1 0 15 10^{15} 1015)次的浮点运算
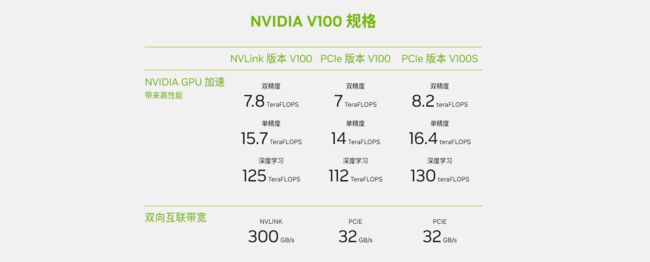
下图展示了大模型训练常用的GPU A100算例
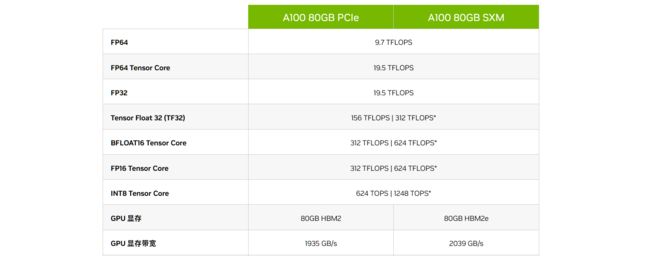
下图展示了最强GPU H100的算力,在双精度情况下基本是V100的5倍。
1.3 带宽
显存和算力是GPU最重要的两个指标,另外一个重要指标就是带宽了。 带宽主要用在分布式训练中通信,带宽小将限制训练速度。
2. 神经网络显存占用
下文将以如下式所示的全连接网络为例进行讲解,其中 X ∈ R n × m X \in R^{n\times m} X∈Rn×m是输入, W ∈ R b × n W \in R^{b\times n} W∈Rb×n 是模型的参数, Y ∈ R b × m Y \in R^{b \times m} Y∈Rb×m 是模型的输出
Y = W X Y=WX Y=WX
那么从上式中可以看出显存的占用主要分为如下几个部分:
- 模型参数:如上式中的 W W W
- 模型的输入输出:如上式中的 X X X 和 Y Y Y
- 优化所需的梯度,即 d W dW dW
- 优化器参数,如动量等
下面将对上述的4个方面进行详细讲解其与batch size的关系
2.1 模型参数
在模型中只有有参数的层,才会有显存占用。这部份的显存占用和输入无关,模型加载完成之后就会占用。对于一个特定的模型,模型参数占用显存是固定的,与 batch size 无关。
通常模型的参数层包括:
- Embedding 层:通常为一个矩阵,参数为 N × M N \times M N×M
- 卷积层:参数为 C i n × C o u t × k × k C_{in} \times C_{out} \times k \times k Cin×Cout×k×k 其中 k k k为卷积核大小
- 全连接层:是一个矩阵,参数为 M × N M \times N M×N,可参考第二章节中的 W W W
- BatchNorm(N):参数为 N N N
2.2 模型的输入输出
注意此处所述的输出不仅仅是模型最后的输出,还包括中间输出,主要表现为各层中间输出的特征。由于当输入的batch size扩大 n n n倍后,输出的矩阵同样扩大 n n n倍,如下表所示2和4分别是batch size的大小, c c c是通道数, m , n m, n m,n分别为图像尺寸,因此模型输出的显存占用,需要计算每一层的feature map的形状(多维数组的形状),显存占用与 batch size 成正比
| 输入shape | 输出shape |
|---|---|
| [2, c, m, n] | [2, c1, m1, n1] |
| [4, c, m, n] | [4, c1, m1, n1] |
2.3 优化器和梯度
以SGD为例对模型进行优化,则参数更新如下式所示:
W t + 1 = W t − α ∇ F ( W t ) W_{t+1}=W_{t}-\alpha\nabla F(W_{t}) Wt+1=Wt−α∇F(Wt)
在SGD中除了要用到参数 W W W还要用到梯度 ∇ F ( W t ) \nabla F(W_{t}) ∇F(Wt),而梯度就是对参数进行求导,梯度占用的显存和参数占用内存相同(参数显存 x2)
当我们换成Momentum-SGD时,由于除了梯度还需要计算动量,所以占用的显存更多,动量占用的显存和参数占用的显存相同(参数显存x3)。
v t + 1 = ρ v t + ∇ F ( W t ) v_{t+1}=\rho v_{t}+\nabla F(W_{t}) vt+1=ρvt+∇F(Wt)
W t + 1 = W t − α v t + 1 W_{t+1}=W_{t}-\alpha v_{t+1} Wt+1=Wt−αvt+1
当我们换成Adam优化器时,Adam算法将动量法和RMSprop结合,Adam 中对一阶动量也是用指数移动平均计算
v t ← β 1 v t − 1 + ( 1 − β 1 ) g t \boldsymbol{v}_{t} \leftarrow \beta_{1} \boldsymbol{v}_{t-1}+\left(1-\beta_{1}\right) \boldsymbol{g}_{t} vt←β1vt−1+(1−β1)gt
s t ← β 2 s t − 1 + ( 1 − β 2 ) g t ⊙ g t \boldsymbol{s}_{t} \leftarrow \beta_{2} \boldsymbol{s}_{t-1}+\left(1-\beta_{2}\right) \boldsymbol{g}_{t} \odot \boldsymbol{g}_{t} st←β2st−1+(1−β2)gt⊙gt占用显存更多,大约为参数显存x4。
3. 计算量
-
对于全连接网络,假设输入维度为 M M M,输出维度为 N N N,batch size为 B B B,那么计算量为 B × N × M B \times N \times M B×N×M
-
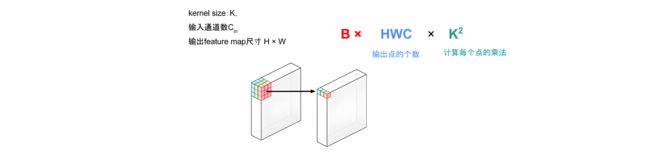
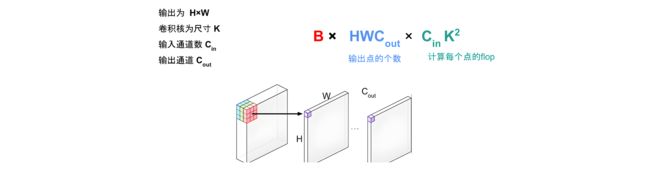
对于卷积网络计算量为 B × H W C o u t × C i n K 2 B \times HWC_{out} \times C_{in}K^2 B×HWCout×CinK2,计算过程如下图所示
4. 结论
根据上述分析,对本文开始提出的几个问题已经有了答案:
首先训练过程不仅受到显存的制约,还与GPU的算力有关,当算力已经被榨干,即使仍然有剩余显存,增大 batch size 也无法加快训练速度。
其次,扩大batch size后显存的占用并不会线性增加,具体哪些部分占用了显存可以参考第二章节的内容。