《python数学实验与建模》(2)高等数学与线性代数
python 数学应用
- 3.1 求下列积分的符号解
(1) ∫ 0 1 1 + 4 x d x \int_{0}^{1}\sqrt{1+4x}~dx ∫011+4x dx (2) ∫ 0 + ∞ e − x sin x d x \int_{0}^{+\infty}e^{-x}\sin x ~dx ∫0+∞e−xsinx dx
from sympy import*#导入sympy的所有函数 x=symbols('x')#创建符号变量 res1=integrate(sqrt(1+4*x),(x,0,1))#积分1 res2=integrate(exp(-x)*sin(x),(x,0,oo))#积分2结果:
− 1 6 + 5 5 6 -\frac{1}{6}+\frac{5\sqrt{5}}{6} −61+655
1 2 \frac{1}{2} 21
3.2 求方程 x 3 − 4 x 2 + 6 x − 8 = 0 x^3-4x^2+6x-8=0 x3−4x2+6x−8=0 的符号解和数值解
from sympy import* from scipy.optimize import fsolve b=solve( x**3-4*x**2+6*x-8,x)#求符号解(求解出来是复数) f=lambda x: x**3-4*x**2+6*x-8 a=fsolve(f,0)#符号解(默认是牛顿迭代法,以0为初值,二阶导函数连续) print(a) print(b.n())#打印数值解
4 3 − 2 9 ( − 1 2 + 3 i 2 ) 64 27 + 2 114 9 3 + ( − 1 2 + 3 i 2 ) 64 27 + 2 114 9 3 \frac{4}{3} - \frac{2}{9 \left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{64}{27} + \frac{2 \sqrt{114}}{9}}} + \left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{64}{27} + \frac{2 \sqrt{114}}{9}} 34−9(−21+23i)32764+921142+(−21+23i)32764+92114
4 3 + 2 9 ( − 1 2 + 3 i 2 ) 64 27 + 2 114 9 3 − ( − 1 2 + 3 i 2 ) 64 27 + 2 114 9 3 \frac{4}{3} +\frac{2}{9 \left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{64}{27} + \frac{2 \sqrt{114}}{9}}} -\left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{64}{27} + \frac{2 \sqrt{114}}{9}} 34+9(−21+23i)32764+921142−(−21+23i)32764+92114
(数值解)array([2.8812394])
3.3 求方程组的符号解和数值解
{ x 2 − y − x = 3 x + 3 y = 6 \left\{ \begin{aligned} x^2-y-x&=3\\ x+3y=6 \end{aligned} \right. {x2−y−xx+3y=6=3
from sympy import* from scipy.optimize import fsolve x,y=symbols('x y') exp1=x**2-y-x-3 exp2=x+3*y-6 print(solve([exp1,exp2],[x,y])) 结果: #[(1/3 - sqrt(46)/3, sqrt(46)/9 + 17/9), (1/3 + sqrt(46)/3, 17/9 - sqrt(46)/9)]
- 3.4 求边值问题 y ′ ′ + y = x cos 2 x , y ( 0 ) = 1 , y ( 2 ) = 3 y^{''}+y=x\cos2x,y(0)=1,y(2)=3 y′′+y=xcos2x,y(0)=1,y(2)=3 的符号解.
from sympy import* y=Function('y')#将y定义为函数 exp=diff(y(x),x)+diff(y(x),x,2)-x*cos(2*x) dsolve(exp,ics={y(0):1,y(2):3})#附上初值条件y ( x ) = x sin ( 2 x ) 10 − x cos ( 2 x ) 5 + 4 sin ( 2 x ) 25 + 13 cos ( 2 x ) 100 + 27 e 2 cos ( 4 ) − 87 − 36 e 2 sin ( 4 ) + 300 e 2 − 100 + 100 e 2 + ( − 213 e 2 + 36 e 2 sin ( 4 ) − 27 e 2 cos ( 4 ) ) e − x − 100 + 100 e 2 y{\left(x \right)} = \frac{x \sin{\left(2 x \right)}}{10} - \frac{x \cos{\left(2 x \right)}}{5} + \frac{4 \sin{\left(2 x \right)}}{25} + \frac{13 \cos{\left(2 x \right)}}{100} + \frac{27 e^{2} \cos{\left(4 \right)} - 87 - 36 e^{2} \sin{\left(4 \right)} + 300 e^{2}}{-100 + 100 e^{2}} + \frac{\left(- 213 e^{2} + 36 e^{2} \sin{\left(4 \right)} - 27 e^{2} \cos{\left(4 \right)}\right) e^{- x}}{-100 + 100 e^{2}} y(x)=10xsin(2x)−5xcos(2x)+254sin(2x)+10013cos(2x)+−100+100e227e2cos(4)−87−36e2sin(4)+300e2+−100+100e2(−213e2+36e2sin(4)−27e2cos(4))e−x
- 3.5已知
A 1 = [ 1 2 3 4 5 6 ] , A 2 = [ 1 1 2 2 3 4 ] , A 3 = [ 2 6 ] , A 4 = [ 3 2 ] A_1=\left[\begin{array}{rrr}1 & 2 \\3& 4\\5 & 6 \end{array}\right] , A_2=\left[\begin{array}{rrr}1 & 1 \\2& 2\\3 & 4 \end{array}\right] , A_3=[2~~6],A_4=[3~~2] A1=⎣ ⎡135246⎦ ⎤,A2=⎣ ⎡123124⎦ ⎤,A3=[2 6],A4=[3 2]
利用Python 分块矩阵的组合,求分块矩阵 A = [ A 1 A 2 A 3 A 4 ] A=\left[\begin{array}{rrr}A_1 & A_2 \\A_3& A_4 \end{array}\right] A=[A1A3A2A4] 的行列式 ∣ A ∣ |A| ∣A∣ .A1=Matrix([[1,2],[3,4],[5,6]]) A2=Matrix([[1,1],[2,2],[3,4]]) A3=Matrix([2,6]).T A4=Matrix([3,2]).T A=A1.col_join(A3).row_join(A2.col_join(A4))#构造A #求|A| print("分块矩阵A:",A) print("|A|:",A.det())# 求行列式
- 3.6 求解下列线性方程组
( 1 ) { x 1 + 2 x 2 + x 3 − x 4 = 0 3 x 1 + 6 x 2 − x 3 − 3 x 4 = 0 5 x 1 + 10 x 2 + x 3 − 5 x 4 = 0 ( 2 ) { 2 x + y − z + w = 1 4 x + 2 y + − 2 z + w = 2 2 x + y − z − w = 1 (1)\left\{ \begin{aligned} x_1+2x_2+x_3-x_4=0\\ 3x_1+6x_2-x_3-3x_4=0\\ 5x_1+10x_2+x_3-5x_4=&0 \end{aligned} \right.\\ \\ (2) \left\{ \begin{aligned} 2x+y-z+w=1\\ 4x+2y+-2z+w&=2\\ 2x+y-z-w=1 \end{aligned} \right. (1)⎩ ⎨ ⎧x1+2x2+x3−x4=03x1+6x2−x3−3x4=05x1+10x2+x3−5x4=0(2)⎩ ⎨ ⎧2x+y−z+w=14x+2y+−2z+w2x+y−z−w=1=2#(1) #1.代数解法(符号解) A=Matrix([[1,2,1,-1],[3,6,-1,-3],[5,10,1,-5]])#创建矩阵 res1=A.nullspace()[0]#非齐次线性方程组(方程的个数小于未知数的个数-无穷多解) res2=A.nullspace()[1] #res1 res2为解空间的基(基础解系) #2.求解方程组 x1,x2,x3,x4=symbols('x1 x2 x3 x4')#创建符号变量 ep1=x1+2*x2+x3-x4 ep2=3*x1+6*x2-x3-3*x4 ep3=5*x1+10*x2+x3-5*x4 result=solve([ep1,ep2,ep3],[x1,x2,x3,x4])#结果为字典 #result: {x1: -2*x2 + x4, x3: 0} #(2) #1.代数解法(符号解) B=Matrix([[1,2,-1,1],[4,2,-2,1],[2,1,-1,-1]]) b=Matrix([[1],[2],[1]]) P=B.row_join(b)#创建增广矩阵 print(P.rref()[0])#初等变换化简增广矩阵-推导出基础解系 #2.求解方程组 x,y,z,w=symbols('x y z w') print(solve([2*x+y-z+w-1,4*x+2*y-2*z+w-2,2*x+y-z-w-1],[x,y,z,w])) #{x: -y/2 + z/2 + 1/2, w: 0}(1)基础解系: [ − 2 1 0 0 ] \left[\begin{array}{rrr}-2 \\1\\0\\0\end{array}\right] ⎣ ⎡−2100⎦ ⎤ [ 1 0 0 1 ] \left[\begin{array}{rrr}1\\0\\0\\1 \end{array}\right] ⎣ ⎡1001⎦ ⎤
(2)化简后的增广矩阵: A = [ 1 1 2 − 1 2 0 1 2 0 0 0 1 0 0 0 0 0 0 ] A=\left[\begin{array}{rrr} 1 & \frac{1}{2} &-\frac{1}{2}&0&\frac{1}{2} \\0& 0&0&1&0\\0&0&0&0&0\end{array}\right] A=⎣ ⎡1002100−21000102100⎦ ⎤ ,基础解系为 [ − 1 2 1 0 0 ] k 1 \left[\begin{array}{rrr}-\frac{1}{2} \\1\\0\\0\end{array}\right]k_1 ⎣ ⎡−21100⎦ ⎤k1 + [ 1 2 0 0 0 ] k 2 +\left[\begin{array}{rrr}\frac{1}{2} \\0\\0\\0\end{array}\right]k_2 +⎣ ⎡21000⎦ ⎤k2 + [ 1 2 0 0 0 ] \left[\begin{array}{rrr}\frac{1}{2} \\0\\0\\0\end{array}\right] ⎣ ⎡21000⎦ ⎤
3.7 先判断下列线性方程组的解的情况,然后求对应的唯一解,最小二乘解或最小范数解
pinv 伪逆:无穷多解时取最小范数解,矛盾方程(无解)时取最小二乘解
( 1 ) { 4 x 1 + 2 x 2 − x 3 = 2 3 x 1 − x 2 + 2 x 3 = 10 11 x 1 + 3 x 2 = 8 ( 2 ) { 2 x + 3 y + z = 4 x − 2 y + 4 z = − 5 3 x + 8 y − 2 z = 13 4 x − y + 9 z = − 6 (1)\left\{ \begin{aligned} 4x_1+2x_2-x_3&=2\\ 3x_1-x_2+2x_3&=10\\ 11x_1+3x_2=8 \end{aligned} \right.\\ \\ (2) \left\{ \begin{aligned} 2x+3y+z=4\\ x-2y+4z=-5\\ 3x+8y-2z=13\\ 4x-y+9z=-6 \end{aligned} \right. (1)⎩ ⎨ ⎧4x1+2x2−x33x1−x2+2x311x1+3x2=8=2=10(2)⎩ ⎨ ⎧2x+3y+z=4x−2y+4z=−53x+8y−2z=134x−y+9z=−6import numpy as np import numpy.linalg as la #(1) #构造矩阵 A=np.array([[4,2,-1],[3,-1,2],[11,3,0]]) b=np.array([2,10,8]).reshape(3,1) print('A的秩=',la.matrix_rank(A))#行列式为零 print('A的行列式=',la.det(A)) #无穷多解 #最小范数解 print('最小范数解:\n',la.pinv(A).dot(b)) #result:A的秩= 2 #A的行列式= 4.440892098500635e-15 (等价于0) #最小范数解: [[ 1.21304348] [-1.44782609] [ 1.95652174]] #(2) A=np.array([[2,3,1],[1,-2,4],[3,8,-2],[4,-1,9]]) b=np.array([4,-5,13,-6]).reshape(4,1) print('A的秩=',la.matrix_rank(A))#行列式为零 #无解(未知数<方程) #最小二乘解 print('最小二乘解:\n',la.pinv(A).dot(b)) #A的秩= 2 #最小二乘解: [[ 0.33333333] [ 1.33333333] [-0.66666667]] #注意!要使用la.solve()求解方程组的函数,必须满足为满秩矩阵
- 3.8 求下列矩阵的特征值和特征向量
A = [ 6 2 4 2 3 2 4 2 6 ] A=\left[\begin{array}{rrr} 6 & 2 &4\\ 2& 3&2\\ 4&2&6\end{array}\right] A=⎣ ⎡624232426⎦ ⎤#符号法构造矩阵 A=Matrix([[6,2,4],[2,3,2],[4,2,6]]) print('A的特征值=',A.eigenvals())#{11: 1, 2: 2} print('A的特征向量=',A.eigenvects())序列解包后的得到的特征向量 ( λ = 2 ) [ − 1 2 1 0 ] (\lambda=2)\left[\begin{array}{rrr} -\frac{1}{2} \\ 1 \\0\end{array}\right] (λ=2)⎣ ⎡−2110⎦ ⎤ , [ − 1 0 1 ] ,\left[\begin{array}{rrr} -1 \\ 0\\1\end{array}\right] ,⎣ ⎡−101⎦ ⎤ ( λ = 11 ) [ 1 1 2 1 ] (\lambda=11)\left[\begin{array}{rrr} 1 \\ \frac{1}{2}\\1\end{array}\right] (λ=11)⎣ ⎡1211⎦ ⎤
- 3.9 已知二次型 f = x 1 2 + x 2 2 + x 3 2 + 2 a x 1 x 2 + 2 x 1 x 2 + 2 x 1 x 3 + 2 b x 2 x 3 , ~f=x_1^2+x_2^2+x_3^2+2ax_1x_2+2x_1x_2+2x_1x_3+2bx_2x_3,~ f=x12+x22+x32+2ax1x2+2x1x2+2x1x3+2bx2x3, 经过正交化变换化为标准型 f = y 2 2 + 2 y 3 2 f=y_2^2+2y_3^2 f=y22+2y32 ,求参数 a , b a,b a,b及所用的正交变换矩阵。
- 二次型矩阵为:
A = [ 1 a + 1 2 1 a + 1 2 1 b 1 b 1 ] A=\left[\begin{array}{rrr} 1 & \frac{a+1}{2} &1\\ \frac{a+1}{2}&1&b\\ 1&b&1\end{array}\right] A=⎣ ⎡12a+112a+11b1b1⎦ ⎤
- 变换后的对角阵为:
[ 0 0 0 0 1 0 0 0 2 ] \left[\begin{array}{rrr} 0& 0&0\\0& 1&0\\0&0&2\end{array}\right] ⎣ ⎡000010002⎦ ⎤
#变换后的对角阵上的元素即为特征值 a,b,c=symbols('a b c') A=Matrix([[x-1,-together((a+1)/2),-1],[-together((a+1)/2),x-1,-b],[-1,-b,x-1]])#构造拉姆达矩阵 ex1=A.det().subs(x,0) ex2=A.det().subs(x,1) ex3=A.det().subs(x,2)#不同特征值带入 #求解非线性方程组(确定参数a,b) a,b=solve([ex1,ex2,ex3],[a,b])[0] print("a:{0},b:{1}".format(a,b))#a:-1,b: 0 #构造实矩阵 B=Matrix([[1,0,1],[0,1,0],[1,0,1]]) #求特征向量 T1,T2,T3=B.eigenvects() L=[T1[2][0],T2[2][0],T3[2][0]] o1=GramSchmidt(L)#施密特正交化方法(实际求出的不同特征值下的特征向量已是正交向量组) #构造正交矩阵 T=o1[0].row_join(o1[1]).row_join(o1[2])最后求得的正交阵为 T = [ − 1 0 1 0 1 0 1 0 1 ] T=\left[\begin{array}{rrr} -1& 0&1\\0& 1&0\\1&0&1\end{array}\right] T=⎣ ⎡−101010101⎦ ⎤
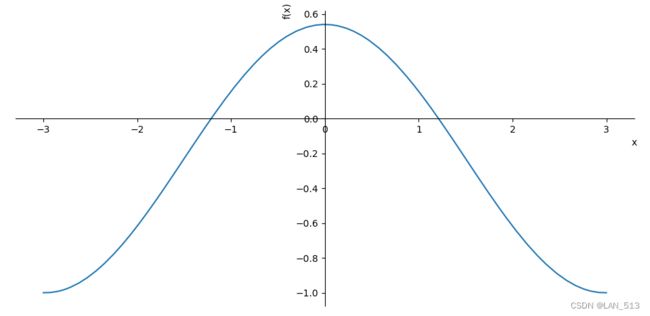
- 3.10 画出 cos x 2 + 1 ~\cos\sqrt{x^2+1}~ cosx2+1 及它在0处的1,3,5阶泰勒展开式在 x ∈ [ − 3 , 3 ] x\in [-3,3] x∈[−3,3]时的图形
from sympy import * x=symbols('x') plot((cos(sqrt(x**2+1))),(x,-3,3)) #泰勒展开 exp=cos(sqrt(x**2+1)) plot(exp,exp.series(x,0,1).removeO(),exp.series(x,0,3).removeO(),exp.series(x,0,5).removeO(),(x,-3,3))
- 3.11 一只兔子在坐标位置(20,0)(单位:m)处以速率 v r = 3 m / s v_r=3 m/s~ vr=3m/s 沿平行于y轴正向的方向奔跑;与此同时,一只猎狗在坐标原点处以速率 v d = 4.5 m / s v_d=4.5m/s vd=4.5m/s追击兔子.猎狗在追击兔子的过程中,方向始终朝向兔子的当前位置.请绘制猎狗追击兔子的近似曲线,并估计追击时间.
#参考CSDN python仿真 import numpy as np from matplotlib.pyplot import * Xr=[20];Yr=[0];vr=3#兔子的水平、竖直位置及速度 Xd=[0];Yd=[0];vd=4.5#猎狗的水平、竖直位置及速度 dt=0.1 L=20 n=0 while L>0.1: Yr.append(dt*vr+Yr[n]) Xr.append(20) X=Xr[n]-Xd[n] Y=Yr[n]-Yd[n] L=np.sqrt(X**2+Y**2)#直角边长 ''' X:水平相对位置 Y:竖直相对位置 L:相对位置 ''' Yd.append(Yd[n]+vd*dt*Y/L)#列表更新 Xd.append(Xd[n]+vd*dt*X/L) n+=1 print('所用时间:%.2f秒'%(n*dt)) plot(Xr,Yr,Xd,Yd) show() #所用时间: 8.10秒秒
- 3.12 分别求下列积分数值解:
(1) ∫ 0 ∞ e − x sin ( x 2 + 2 ) d x \int_{0}^{\infty}e^{-x}\sin(\sqrt{x^2+2})dx ∫0∞e−xsin(x2+2)dx
(2) ∬ D ( x 2 + 2 y 2 ) d x d y \iint\limits_D(x^2+2y^2)dxdy D∬(x2+2y2)dxdy 其中 D D D是由曲线 x = y 2 , y = x − 2 x=y^2,y=x-2 x=y2,y=x−2 所围成的平面区域.
(3) ∭ Ω z d x d y d z , \iiint\limits_\Omega zdxdydz, Ω∭zdxdydz, 其中 Ω ~\Omega~ Ω 是由曲面 z = x 2 + y 2 z=x^2+y^2 z=x2+y2 与平面 z = 4 z=4 z=4 所围成的闭区域
#一重积分(默认辛普森积分法) #定义函数 import numpy as np from scipy.integrate import quad f=lambda x:np.exp(-x)*np.sin(np.sqrt(x**2+2)) print("I1:",quad(f,0,np.inf)[0]) #先将该积分化为累次积分(抛物线与直线围成的区域) f2=lambda y,x:x**2+2*y**2 print('I2:',dblquad(f2,1,4,-1,2)[0]) #三重积分(在椭圆抛物面与平面围成的区域上积分) f3=lambda z,y,x: z F=lambda x:np.sqrt(4-x**2) print('I3:',tplquad(f3,-2,2,lambda x:-F(x),lambda x:F(x),0,4)[0] ) #结果 I1: 0.8328534212790222 I2: 81.0 I3: 100.53096491487351
- − 1 ≤ y ≤ 2 , 1 ≤ x ≤ 4 -1\le y\le 2,1\le x \le 4 −1≤y≤2,1≤x≤4
- ∫ − 2 2 d x ∫ − 4 − x 2 4 − x 2 d y ∫ 0 4 z d z \int_{-2}^{2}dx\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}dy\int_{0}^4zdz ∫−22dx∫−4−x24−x2dy∫04zdz
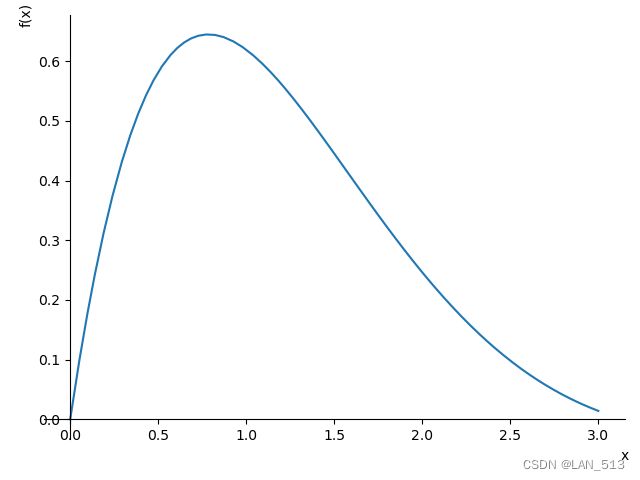
- 3.13 求函数 f ( x ) = 2 e − x s i n x f(x)=2e^{-x}sinx f(x)=2e−xsinx在[0,3]上的极小点和极大点
from scipy.optimize import * import numpy as np from sympy import * x=symbols('x') y=2*exp(-x)*sin(x) print('极大点:'solve(diff(y,x),x)[0])#为极值点 pi/4 f=lambda x:2*np.exp(-x)*np.sin(x) print('极小点:',fminbound(f,0,3))#非极值点,但是为区间上的最小值点 2.9999965472915386 #plot(y,(x,0,3))可以绘制图像观察如下:
- 3.14 某容器内侧是由曲线 x 2 + y 2 = 4 y ( 1 ≤ y ≤ 3 ) x^2+y^2=4y~~(1\le y\le3) x2+y2=4y (1≤y≤3) 与 x 2 + y 2 = 4 ( y ≤ 1 ) x^2+y^2=4(y\le 1) x2+y2=4(y≤1)绕y轴旋转一周而形成的曲面.
- 求容器的体积
- 若将容器内盛满的水从容器底部全部抽出,至少需要多少功?(长度单位为m,重力加速度 g = 9.8 m / s 2 , 水的密度 ρ = 1 0 3 k g / m 3 g=9.8 m/s^2,水的密度\rho=10^3kg/m^3 g=9.8m/s2,水的密度ρ=103kg/m3)
1. 容器体积:(旋转曲面积分) π 2 ∫ a b f ( x ) 2 d x \frac{\pi}{2}\int_{a}^{b}f(x)^2dx 2π∫abf(x)2dx π 2 ∫ − 2 1 4 − y 2 d y + π 2 ∫ 1 3 4 − ( y − 1 ) 2 d y \frac{\pi}{2} \int_{-2}^{1}4-y^2dy+\frac{\pi}{2}\int_{1}^{3}4-(y-1)^2dy 2π∫−214−y2dy+2π∫134−(y−1)2dy
2.功的微元: d W = m g h = ρ g h V ( ρ = m V ) = ρ g h S ( x ) d x ~dW=mgh=\rho ghV(\rho=\frac{m}{V})=\rho ghS(x)dx dW=mgh=ρghV(ρ=Vm)=ρghS(x)dx (h 为将该微元体积的水抽到容器口的位移)
W = ∫ 1 3 ρ g π ( 3 − y ) ( 4 y − y 2 ) d y + ∫ − 2 1 ρ g π ( 4 − y 2 ) ( 3 − y ) d y W= \int_{1}^{3}\rho g\pi(3-y)(4y-y^2)dy+\int_{-2}^{1}\rho g\pi(4-y^2)(3-y)dy W=∫13ρgπ(3−y)(4y−y2)dy+∫−21ρgπ(4−y2)(3−y)dy
import numpy as np from sympy import * #注意积分只是一半的体积(x负半轴也要考虑) res=integrate((4-y**2),(y,-2,1))+integrate((4-(y-1)**2),(y,1,3))*np.pi/2*2 print("容器的体积为:",res)#25.7551608191456 exp1=12*y-3*y**2-4*y**2+y**3 exp2=(4-y**2)*(3-y) res1=(integrate(exp2,(y,-2,1))+integrate(exp1,(y,1,3)))*10**3*9.8*np.pi print('做功为:%eJ'%res1)#科学计数法 1.126313e+06 J(焦耳)
3.15 (1)一架重 5000 k g 5000kg 5000kg的飞机以 800 k m / h 800km/h 800km/h的航速开始着陆,在减速伞的作用下滑行 500 m 500m 500m后减速为 100 k m / h 100km/h 100km/h.设减速伞的阻力与飞机的速度成正比,并忽略飞机所受的其他外力,试计算减速伞的阻力系数
f = k v = − m a , − a = k m v = d v d x × d x d t = v d v d x , d x = m k d v , m k ∫ v 0 v 1 d v = − x ( 位移 ) f=kv=-ma,-a=\frac{k}{m}v=\frac{dv}{dx}\times\frac{dx}{dt}=v\frac{dv}{dx},dx=\frac{m}{k}dv,~\frac{m}{k}\int_{v_0}^{v_1}dv=-x(位移) f=kv=−ma,−a=mkv=dxdv×dtdx=vdxdv,dx=kmdv, km∫v0v1dv=−x(位移)
(2)将同样的减速伞配备在 8000 k g 8000kg 8000kg的飞机上,现已知机场跑道长度为 1200 m 1200m 1200m,若飞机着陆速度为 600 k m / h 600km/h 600km/h,问跑道长度是否能否保障飞机安全着陆
from sympy import * #求积分 v=symbols('v') k=(5000*integrate(1,(v,800,100))/3.6)/(-500)#统一为国际单位 print('阻力系数f={}'.format(k))#阻力系数f=1944.44444444444 #反推:求末速度=0时的位移 M=8000 x=-(M/k)*(0-600)/3.6 print(x)#685.714285714286<1200 可以安全着陆
- 3.16 求函数 f ( x 1 , x 2 ) = 100 ( x 2 − x 1 2 ) 2 + ( 1 − sin ( x 1 ) ) 2 cos ( x 2 ) f(x_1,x_2)=100(x_2-x_1^2)^2+(1-\sin(x_1))^2\cos(x_2) f(x1,x2)=100(x2−x12)2+(1−sin(x1))2cos(x2) 的局部极小点.
import numpy as np from scipy.optimize import minimize f=lambda x:100*(x[1]-x[0]**2)**2+(1-np.sin(x[1]))**2*np.cos(x[1]) x0=minimize(f,[0,0]) print('函数的局部极小点={0},极小值为{1}'.format(x0.x,x0.fun)) #结果: 函数的局部极小点=[2.99920288e-08 9.94829962e-03],极小值为0.9900510566055519