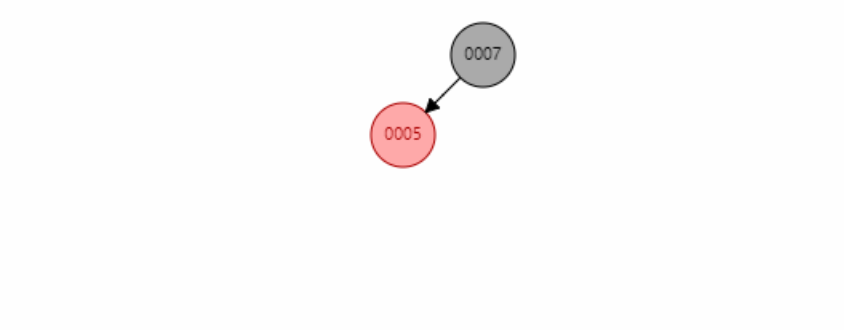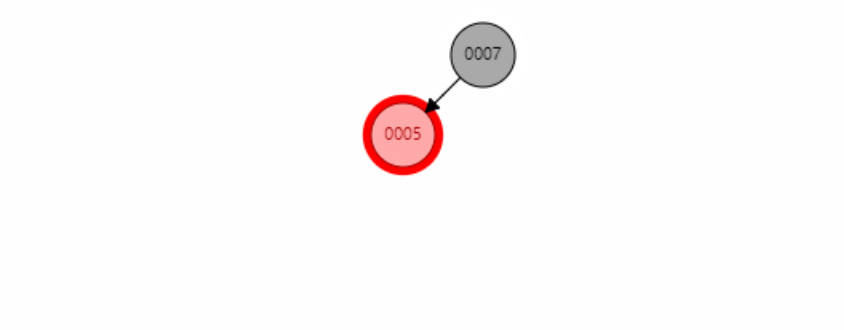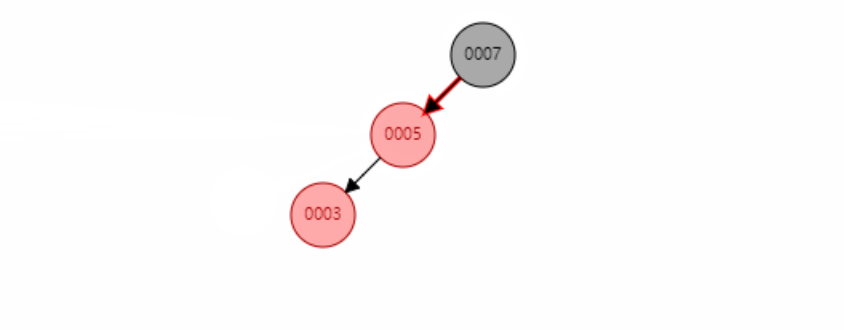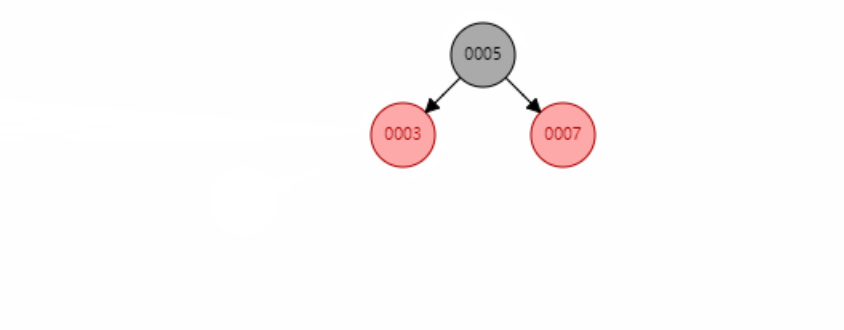
手撕TreeMap红黑树
红黑树
-
- 红黑树优势到底在哪
- 红黑树和234树的映射关系
-
- 什么是234B
- 234节点的对应
- 234树的生长
- 234树的删除
- 映射关系
- 转化Test
- 红黑树性质
- 节点类和基本方法
- 红黑树的左右旋
-
- 左旋图1
- 左旋图2
- 左旋代码
- 右旋图
- 右旋代码
- 新增节点
-
- AVL树方法搜索位置
- 红黑插入的情况图解(以左为例)
- 红黑插入的情况图流程图
- 代码详解
- 新增代码整合(put)
- 删除节点
-
- 寻找该节点(getNode)
- 删除定位节点(deleteNode)
-
- 删除节点情况分析
- 代码分解
-
- 情况三
- replace的分析和确定
- if处理情况二
- else处理情况一
- 代码deleteNode整合
- 删除后的平衡调整(fixAfterRemove)
-
- 兄弟为黑色有红子节点 情况1---3
- (假)兄弟为红色 情况 4
- 兄弟为黑色且无红节点 情况5
-
- 七个思考:
- 代码
- 思考:父节点红且兄弟无红色子节点
-
- 思路
- 图解
- fixAfterRemove流程图
- 整合调整的代码(fixAfterRemove)
- 三种方法整合(remove)
- 删除代码整合
- 完整代码和测试
-
- RBTreeTest
- TreeOperation
- RBTree
红黑树测试连接
234树测试链接
红黑树优势到底在哪
红黑树的查询性能略微逊色于AVL树,因为红黑树比AVL树会稍微不平衡,造成多出一层来,也就是说红黑树的查询性能只比相同内容的avl树最多多出一次的比较。但是:红黑树在插入和删除上基本可以完虐AVL树,AVL树每次插入删除会进行大量的平衡度计算,而对于红黑树依照维持红黑性质所做的红黑变换和旋转操作所需要的开销相较于AVL树要小得多。红黑树最多使用三次旋转能完成所有的添加和删除操作。
红黑树和234树的映射关系
什么是234B
234树特点:
- 严格的平衡树
- 在每个节点上没有子节点或者有且仅有与之对应的子节点数量
- 每一个叶子节点对应的树的层数是一定的
- 遵循向上生长的原则
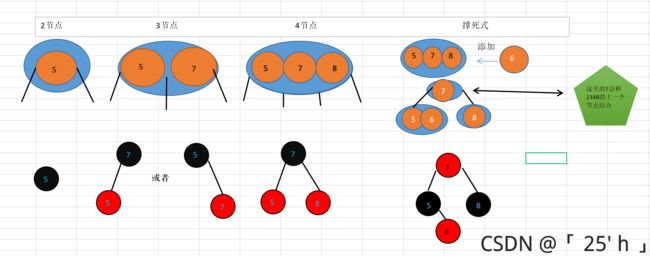
234节点的对应
每一个蓝色底盘就是一个234树的一个节点,每个节点中的每个橙色就是一个节点中的元素。在填充234树时要么没有子节点要么将节点中的每个黑色线均填充子节点,否则就不满足B树平衡.

234树的生长
- 添加元素时会进行查找到合适的位置,放在适合的节点
- 若加上该元素后该节点中有了四个元素(5节点式),就要将原来的节点中三个元素中间的元素作为父节点上提,并将对于原节点左右元素分别作为父节点左右子节点
- 对于上提的父节点与原节点父节点元素结合,若结合后是四个元素,重复步骤 2
234树的删除
映射关系
- 一个红黑树只对应一个234树,一个234树可能对应多个红黑树。
- 红黑树的红色节点不可能连续
- 一个234树中的节点对应到红黑树上只有一个黑色节点,因此在红黑树的任意节点到该节点的叶子节点路径上黑色节点个数一定是一样的
转化Test
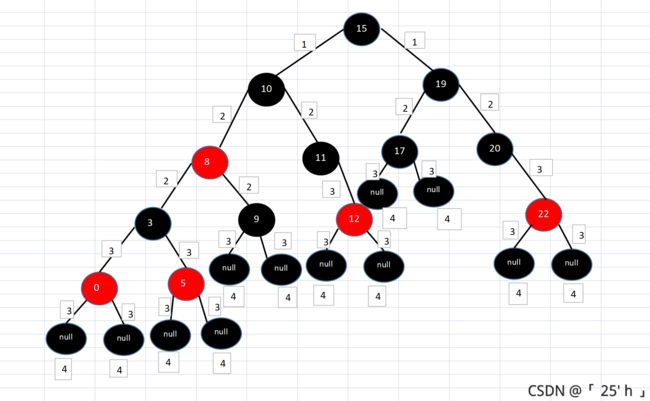
这是一个带颜色的234树:

转化为红黑为:(标号为该路径上有几个黑色节点)

红黑树性质
- 节点为红色和黑色
- 根节点为黑色
这两条可理解为红黑树定义
- 所有叶子均为黑色
对这一条可能有些疑问,实际上在处理红黑树的的节点时,若该节点为叶子节点,就会在后边填补俩个黑色空节点,在上述举例时只不过被省略了。
- 左右红色节点下均有两个黑色节点
第三条的介入时只成立
- 从任意节点到该节点所有的叶子节点的简单路径上的黑的节点个数一定(黑色平衡)
根据234树的平衡,每个节点对应在红黑树的节点时有且只有一个黑色节点
节点类和基本方法
public class RBTree<K extends Comparable<K>,V>{
private RBNode root;//先定义根节点
private static final boolean BLACK=true;//黑色为真
private static final boolean RED=false;//红色为假
//获取节点颜色
private static boolean getColor(RBNode rbNode){
//空节点时为黑,因为最后层为黑
//这样可以避免在后续复杂处理时出现空指针
return rbNode==null?BLACK:rbNode.color;
}
//设置节点颜色
private static void setColor(RBNode rbNode, boolean b){
if(rbNode!=null){
rbNode.color=b;
}
}
//获取父节点
private static RBNode parentOf(RBNode rbNode){
return rbNode==null?null:rbNode.parent;
}
//获取左子节点
private static RBNode leftOf(RBNode rbNode){
return rbNode==null?null:rbNode.left;
}
//获取右子节点
private static RBNode rightOf(RBNode rbNode){
return rbNode==null?null:rbNode.right;
}
//节点类放在了RBTree类中当作了内部类
//该类的泛型K键值(TreeMap中的键)继承Comparable接口,用于后续比较
static class RBNode<K extends Comparable<K>,V>{
K key;
V value;
private boolean color;
RBTree.RBNode parent;//父亲节点
RBTree.RBNode left;//左节点
RBTree.RBNode right;//右节点
//创建构造器
public RBNode(K key, V value, RBTree.RBNode parent) {
this.key = key;
this.value = value;
this.color = BLACK;
this.parent = parent;
}
//可自己调用前序遍历时显示键值对的值
@Override
public String toString() {
return "RBNode{" +
"key=" + key +
", value=" + value +
", color=" + (color?"BLACK":"RED") +
'}';
}
//一些 get set 方法
public RBTree.RBNode getLeft() {
return left;
}
public RBTree.RBNode getRight() {
return right;
}
public boolean isColor() {
return color;
}
public V getValue() {
return value;
}
}
}
关于为什么有这些私有方法,是因为在后续过程中不管是左右旋,还是节点颜色判断将不会担心空指针异常。
红黑树的左右旋
左旋图1
左旋图2
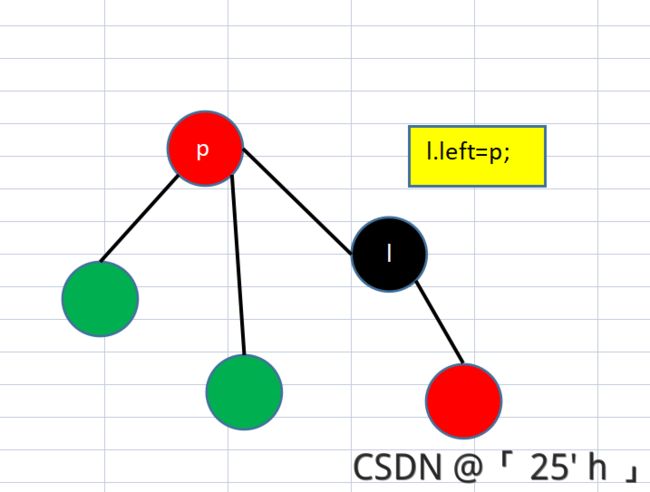
- p节点为以p节点进行左旋转
- 蓝色箭头为该子树的父节点
- 绿色节点为颜色位置的节点,可能为空
注:每一次左右节点的交换都要改变父亲父节点的指向,同时要注意父亲节点的左还是右指向该孩子节点,上图省略了
于是有了下面代码:
左旋代码
//以p节点为旋转点
private void leftRotate(RBNode p) {
if(p!=null){
RBNode l=p.right;
setColor(l, p.color);
setColor(p, RED);
p.right = l.left;
//上句交换了指向,所以要修改父节点指向,方向已知
if (l.left != null) {
l.left.parent = p;
}
l.parent = p.parent;
//上句交换了指向,所以要修改父节点指向,方向未知,所以要判断方向
if (p.parent == null) {//若无说明p节点为根节点,让根节点指向l即可
root = l;
} else if (p.parent.left == p) {//若是父节点左
p.parent.left = l;
} else {//若是父节点右
p.parent.right = l;
}
l.left = p;
//处理父节点,且不可能为空
p.parent = l;
}
}
右旋图
右旋代码
同理左旋,不在赘述
private void rightRotate(RBNode p) {
RBNode r = p.left;
setColor(r, getColor(p));
setColor(p, RED);
p.left = r.right;
if (r.right != null) {
r.right.parent = p;
}
r.parent = p.parent;
if (p.parent == null) {
root = r;
} else if (p.parent.left == p) {
p.parent.left = r;
} else {
p.parent.right = r;
}
r.right = p;
p.parent = r;
}
新增节点
AVL树方法搜索位置
在RBTree类中创建put方法,先进行查找:
class RBTree<K extends Comparable<K>,V>{
public void put(K key,V value){
if(key==null){
throw new RuntimeException("空指针异常");
}
//若root为空,说明第一个元素,那么直接对root修改
if(null == root){
//颜色默认黑
root=new RBNode<>(key,value==null?key:value,null);
return;
}
//com记录比较值,用于记录插入节点的位置是父节点的方向左还是右
int com;
//记录插入节点的父节点,因为插入节点不可能立即成为根结点(后续调整可能成为父节点),所以父节点必存在
RBNode parentTail;
//从根节点开始搜索,parentTail紧跟其后
RBNode tail=root;
do{
//记录父节点
parentTail=tail;
//将插入值和tail搜索的值及进行比较,用com记录
com=key.compareTo((K) tail.key);
if(com<0){
//向左搜索
tail=leftOf(tail);
}else if (com>0){
//向右搜索
tail=rightOf(tail);
}else {
//若相同就直接覆盖当前值,因为并未改变树的平衡,并直接结束程序
tail.value=value==null?key:value;
return;
}
}while (tail!=null);//终止搜索条件
//创建一个新节用于存储进来的数据
RBNode newRBNode=new RBNode<>(key,value==null?key:value,parentTail);
//根据com大小进行父节点的左右赋值操作
if (com<0){
parentTail.left=newRBNode;
}else {
parentTail.right=newRBNode;
}
}
fixAfterPut(newRBNode);
}
是不是以为这样就完了?(怎么可能有一句代码我还没见过!!!)
那我们就看看用AVL搜索后的结果可能出现的所有情况吧!
红黑插入的情况图解(以左为例)
根据插入节点对应在234树上的情况有:
- 添加的颜色要优先置为红,防止直接对红黑树平衡造成影响
- 在父节点为黑色的时候,无需操作。
- 父亲节点为红时,就要判断叔叔节点是否存在
- 叔叔节点不存在(第三种),判断该节点是父亲什么节点做一次或两次旋转
- 叔叔节点存在就转换颜色(第四种),将爷爷节点作为新节点判断进入循环
- 根置黑
红黑插入的情况图流程图
![]()
代码详解
关于root空的这一种情况在查找前已经排除。
private void fixAfterPut(RBNode newRBNode) {
//将新增节点置为红色
setColor(newRBNode,RED);
//若新增节点的父节点为黑,直接退出
//若没有这个判断也可,因为不会进入循环,不过这样好理解
if(getColor(parentOf(newRBNode))==BLACK){
return;
}
//新增节点不为根节点,且父节点为红色
//(父节点为红色是作为出循环条件,毫无影响第一次进循环
while (newRBNode != root&&getColor(parentOf(newRBNode))==RED){
//添加指向爷爷和父亲的指针,便于理解
RBNode grandFather=parentOf(parentOf(newRBNode));
RBNode father=parentOf(newRBNode);
//判断父亲是爷爷的左节点还是右节点,依次判断叔叔在爷爷节点的左右
if(leftOf(grandFather)==father){
//确定叔叔节点,可能为null
RBNode uncle=rightOf(grandFather);
//叔叔节点空还是红
//(不可能为黑,若黑那么之前的树不平衡)
if(getColor(uncle)==RED){
//撑死式换颜色
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
//将爷爷换成新增节点,重新循环
newRBNode=grandFather;
}else {//叔叔节点空:
//是否需要进行左旋调整
if(rightOf(father)==newRBNode){
leftRotate(father);
//指向新节点位置
newRBNode=father;
}
//根据爷爷节点右旋即可
//右旋后newRBNode节点的父亲就是黑色了
//这里不需要手动变颜色,因为在旋转时已经变过了,不过要小心验证
rightRotate(grandFather);
}
}else {//跟上一段代码雷同
RBNode uncle=leftOf(grandFather);
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(leftOf(father)==newRBNode){
rightRotate(father);
newRBNode=father;
}
leftRotate(grandFather);
}
}
}
//将根节点置为黑,防止其他操作变成了红色
setColor(root,BLACK);
}
新增代码整合(put)
public void put(K key,V value){
if(null == root){
root=new RBNode<>(key,value==null?key:value,null);
return;
}
int com;
RBNode tail=root;
RBNode parentTail;
if(key==null){
throw new RuntimeException("空指针异常");
}
do{
parentTail=tail;
com=key.compareTo((K) tail.key);
if(com<0){
tail=leftOf(tail);
}else if (com>0){
tail=rightOf(tail);
}else {
tail.value=value==null?key:value;
return;
}
}while (tail!=null);
RBNode newRBNode=new RBNode<>(key,value==null?key:value,parentTail);
if (com<0){
parentTail.left=newRBNode;
}else {
parentTail.right=newRBNode;
}
fixAfterPut(newRBNode);
}
private void fixAfterPut(RBNode newRBNode) {
setColor(newRBNode,RED);
while (newRBNode != root&&getColor(parentOf(newRBNode))==RED){
RBNode grandFather=parentOf(parentOf(newRBNode));
RBNode father=parentOf(newRBNode);
if(leftOf(grandFather)==father){
RBNode uncle=rightOf(grandFather);
//空或者黑色不进入
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(rightOf(father)==newRBNode){
leftRotate(father);
newRBNode=father;
}
rightRotate(grandFather);
}
}else {
RBNode uncle=leftOf(grandFather);
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(leftOf(father)==newRBNode){
rightRotate(father);
newRBNode=father;
}
leftRotate(grandFather);
}
}
}
setColor(root,BLACK);
}
删除节点
删除的步骤:
- 获取对应的Key值的被删除节点(getNode)
- 确定删除节点后通过一个函数进行删除操作(deleteNode)
- 再创建一个函数用于删除后对红黑树的平衡调整(fixAfterRemove)
- 将上述的三种方法整合(remove)
寻找该节点(getNode)
寻找的方法并没有对红黑树平衡有任何影响,所以可以看成AVL树进行查询。直接看代码
private RBNode getNode(K key){
RBNode tail=root;//起始为根节点的指针用于后续的查找定方向
if(root==null){
//root空就不可能有对应的值
throw new RuntimeException("不可能空");
}
//查找的节点不为空就继续向左右查找
while (tail!=null){
//通过比较进行左右的位置确定
int cmp=key.compareTo((K)tail.key);
if(cmp<0){
//向左查找
tail=leftOf(tail);
}else if (cmp>0){
//向右查找
tail=rightOf(tail);
}else {
//说明查找到结果,就讲该值返回
return tail;
}
}
//出了循环就意味着没有该值,返回空
return null;
}
删除定位节点(deleteNode)
删除节点情况分析
注:node为删除节点,replace表示node删除后代替node的节点
情况一:删除节点无子节点
注:情况一和情况二下删除节点node为红时均不需要调整,只有是黑的才调整!!!
代码分解
因为情况三最终都会通过前驱后后继转到情况一或情况二。所以我们只需要在进行情况一情况二前进行情况三的讨论。
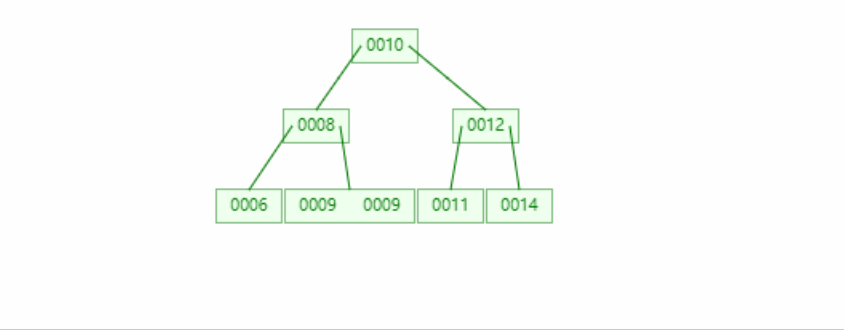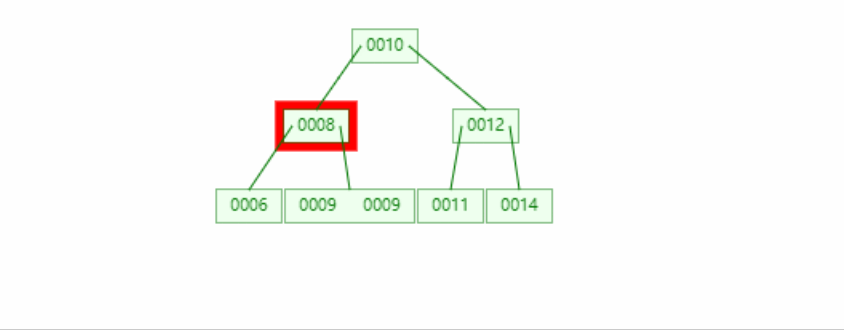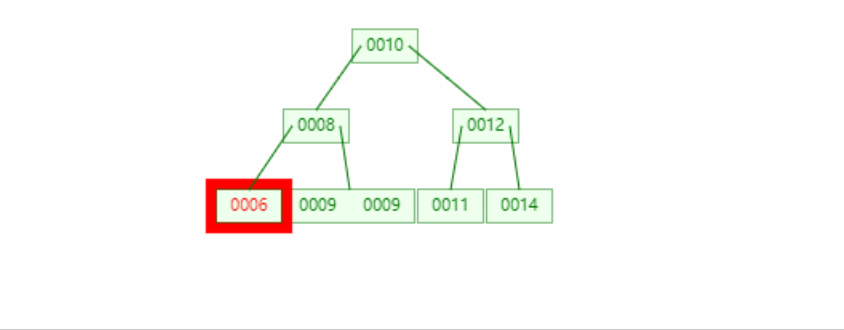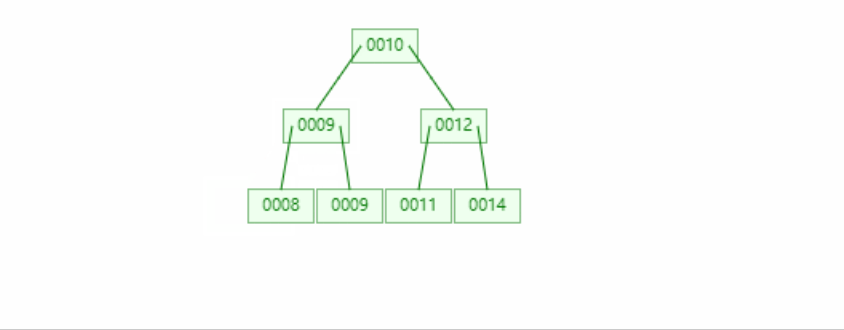
情况三
前驱节点
//node为需要被删除的节点,寻找它的前驱节点。
private RBNode pre(RBNode node){
//由于比node小的在node的左边,而这些值最大的在node左子树的最右边
//由于node节点有两个子节点,所以无需判断node左是否为空
RBNode l=leftOf(node);
//向右找最大值
while (l.right!=null){
l=l.right;
}
return l;
}
后继节点
private RBNode suc(RBNode node){
//由于比node大的在node的右边,而这些值最小的在node右子树的最左边
//由于node节点有两个子节点,所以无需判断node右是否为空
RBNode r=rightOf(node);
while (r.left!=null){
r=r.left;
}
return r;
}
情况三---->情况一二
if(leftOf(node)!=null&&rightOf(node)!=null){
RBNode pre = pre(node);//这里使用前驱节点
//进行赋值,因为pre在赋值node后就会作为新的node被删除,所以它的值不重要
node.key=pre.key;
node.value=pre.value;
//后继节点作为新的被删除节点
node=pre;
}
replace的分析和确定
replace作为node删除后代替node的节点,该如何确定呢?
- 在node有节点时指向非空节点(情况二)
- 若无节点,就指向null(情况一)
写法一
RBNode replace;
//当左空右不空,replace指向右(情况二)
if(leftOf(node)==null&&rightOf(node)!=null){
replace=rightOf(node);
//当右空左不空,replace指向左(情况二)
}else if (leftOf(node)!=null&&rightOf(node)==null){
replace=leftOf(node);
}else {//左右都空(情况一)
replace=null;
}
/*
leftOf(node)!=null&&rightOf(node)!=null情况去哪了?
这种情况为情况三的,在前面已经转换为了情况一或二所以不可能存在
*/
写法二
写法一的代码写成三目操作符是这样的:
RBNode replace=leftOf(node)!=null?leftOf(node):rightOf(node);
if处理情况二
//现在只剩情况一和二,关于情况一和二的区别就是replace是否为null
if(replace!=null){//情况二进入
//将node父节点(是否存在和左右不定,需要讨论)的子节点指向replace
//以达到删除node的效果
replace.parent=parentOf(node);
//当情况二下删除的节点node是根节点时(情况三不可能,因为转换成删除前驱结点不可能为根节点)
//此时根节点下只有一个红色节点,replace为红色节点
//parentOf(node)为空,replace.parent也为null
//所以要判断node是否为根节点,即判断parentOf(node)==null是否成立
if(parentOf(node)==null){
//若是根节点yong红色replace替换,在后来因为删除的node为黑会调整颜色
root=replace;
}else if(node==leftOf(parentOf(node))){//删除节点为父节点的左子节点
node.parent.left=replace;
}else {//删除节点为父节点的右子节点
node.parent.right=replace;
}
//处理掉和删除节点node的所有指针关系
node.left=node.right=node.parent= null;
//❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤调整B❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤
//情况二下的删除节点为黑色,包含了删除节点为根节点情况
if(getColor(node)==BLACK){
//replace!=null已判断成立,那么该replace节点必为红色
//因为原来的node节点只有一个方向有子节点,这个子节点就是replace,为保持黑色平衡所以为红
//实际上这种情况只要一句话就可以了,不过为了模块化放在了函数里
//进入fixAfterRemove后因为replace必定为红,所以进入不了fixAfterRemove中的循环(fixAfterRemove函数在后面)
fixAfterRemove(replace);
/*
如果进入fixAfterRemove处理也可以,只需要直接将replace变为黑色
用下面这句话代替 fixAfterRemove
setColor(replace,BLACK);
❤❤❤❤❤❤❤❤❤建议用setColor(replace,BLACK);这样可以更好的理解
*/
}
}
else处理情况一
//进入else意味着需要删除的节点node无子结点,就是情况一
//由于无子节点,这里replace==null,仅仅提示一下,好像没什么用
else {
//❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤调整A❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤
//红色时无需调整只要进行子节点和父节点的指针调整就行
//node黑色才进入调整
if(getColor(node)==BLACK){
fixAfterRemove(node);
}
//调整后对于子节点父节点指针调整
//But你怎么知道他有父节点?所以要讨论
if(parentOf(node)!=null) {
if (node == leftOf(parentOf(node))) {//删除节点右节点为后继
node.parent.left = null;
} else {
node.parent.right = null;
}
node.parent = null;
}else {
//node没有父节点就是根节点,并且无子节点
//说明要删除根节点,就要直接变空
root=null;
}
}
注:将上面的代码按顺序放在函数名为deleteNode里面就好了
代码deleteNode整合
private RBNode deleteNode(RBNode node) {
if (leftOf(node) != null && rightOf(node) != null) {
RBNode pre = pre(node);
node.key = pre.key;
node.value = pre.value;
node = pre;
}
RBNode replace = leftOf(node) != null ? leftOf(node) : rightOf(node);
if (replace != null) {
replace.parent = parentOf(node);
if (parentOf(node) == null) {
root = replace;
} else if (node == leftOf(parentOf(node))) {
node.parent.left = replace;
} else {
node.parent.right = replace;
}
node.left = node.right = node.parent = null;
if (getColor(node) == BLACK) {
fixAfterRemove(replace);
}
}
else {
if (getColor(node) == BLACK) {
fixAfterRemove(node);
}
if (parentOf(node) != null) {
if (node == leftOf(parentOf(node))) {
node.parent.left = null;
} else {
node.parent.right = null;
}
node.parent = null;
} else {
root = null;
}
}
return null;
}
删除后的平衡调整(fixAfterRemove)
hahahahahahahaha最难理解的红黑调整,它来了!!!

牢记:
1.删除节点为黑色,这里用黄色表示
2.这里只举例删除节点为父节点左子节点的情况
3.我们的代码在 左 / 右 旋的时候能改变颜色,将被绕着旋转的节点颜色给 右 / 左 子节点后自己变成红色
什么时候才需要调整?
答:删除节点为黑色,并且该黑节点无子节点
调整的根本目标是什么?
答:寻找能被移动的节点(红色),变成黑色来弥补我们删除黑色节点的一侧带来的黑色不平衡问题。
兄弟为黑色有红子节点 情况1—3
- 这种黑色兄弟节点对应在234树中为兄弟节点。
- 兄弟节点无子红节点在最后讨论
- 兄弟节点的子节点不可能是黑色,因为不平衡。
- 删除节点为4黑色,用黄色表示删除的节点
问题:关于为什么父节点可以是红色或黑色?
在进行左右旋的时候原来父节点的颜色会保留在旋转后的父节点中,原来的父节点会变成红色,所以不会影响整体黑色节点层数。
//因为假设的是删除节点为父节点的左,所以兄弟必为右
RBNode rBro=rightOf(parentOf(node));
//getColor(leftOf(rBro))==RED这句话在后来可以省略,因为我们在后来优先判断兄弟节点左右均为黑
//借点空的时候默认返回BLACK
if(getColor(rightOf(rBro))==BLACK&&getColor(leftOf(rBro))==RED){
//左旋兄弟节点
rightRotate(rBro);
//将指针指向当前兄弟节点
rBro=rightOf(parentOf(node));
}
//进行左旋
leftRotate(parentOf(node));
//平衡颜色
setColor(parentOf(node),BLACK);
setColor(rightOf(rBro),BLACK);
(假)兄弟为红色 情况 4
问:为什么不能让兄弟为红的节点转到左边变成黑色?
答:若兄弟为红色,那么该红色节点下必定是两个黑色,如果该红色直接走了,那么两个黑色节点无法处理,所以要左旋变成兄弟为黑色。
为什么叫做假兄弟?
答: 该红色节点在234树中为父亲的元素

//判断是否是真正的兄弟,RED颜色就是假的兄弟,该兄弟节点在234树上为父亲的
if(getColor(rBro)==RED){
//绕父亲节点左旋
leftRotate(parentOf(node));
//将指针调整为真兄弟
rBro=rightOf(parentOf(node));
}
兄弟为黑色且无红节点 情况5
在聊该情况前我们有几个思考:
七个思考:
思考一:什么时候存在兄弟为黑色且无红节点这种情况?
答: (假)兄弟为红色 情况 4 旋转之后,后者本来就存在。所以该判断必定在 (假)兄弟为红色 情况 4之后
思考二:删除该黑色节点对对应的234树有什么影响?
答:映射在234树上就相当于删除了其中的一整个节点,造成了234树不平衡。
思考三:234树处理的大致思路是什么?
答:将删除节点路径上增加一个节点(该节点值间接的来自兄弟节点中的元素)或者将整个树减少一层。234树中的节点对应着红黑树中黑色节点
思考四:若节点间接来自兄弟节点,那么就会将4节点变成3节点,3节点变成2节点,但是兄弟节点原来的子节点数量却保持不变,不会使树不遵守B树原则吗?
答:不会,我们在将兄弟节点的值间接变成删除树节点的时候有一个子树的父节点发生了变化(注意-76的父亲节点)。这在红黑树中对应着左右旋操作(并非一定是一次)
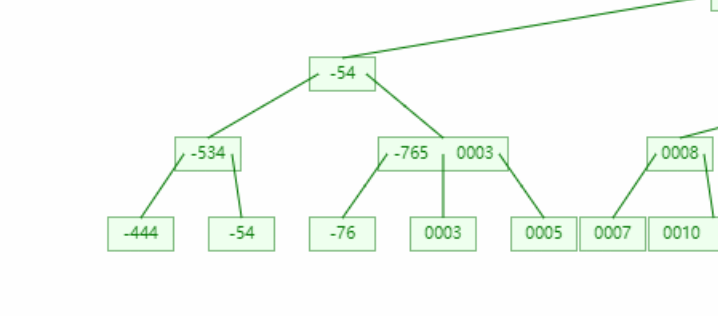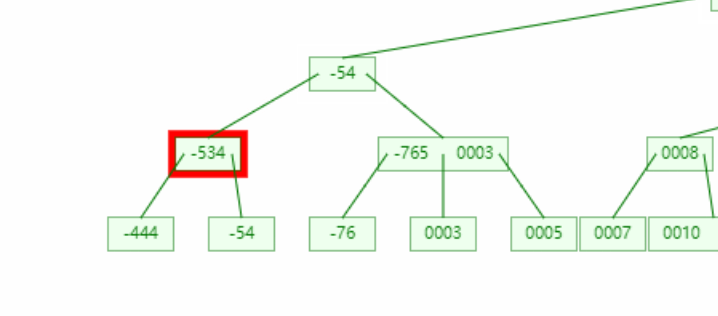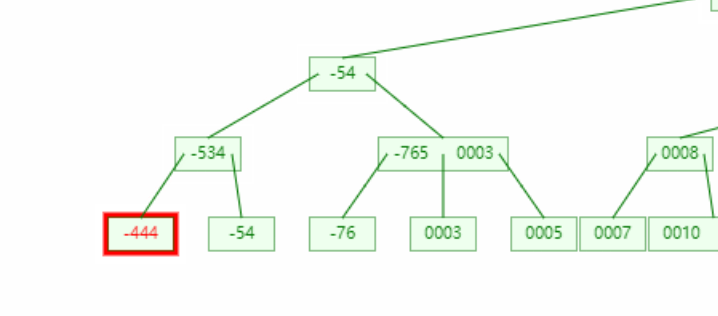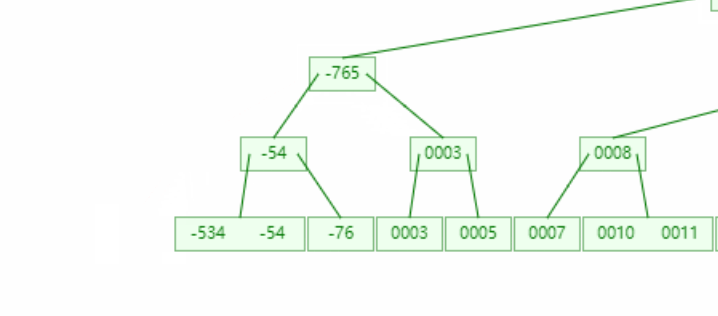
思考五:那么增加节点的问题234树自己怎么处理的?
答:寻找删除节点的兄弟节点,若兄弟节点大于1的元素,就会对这个兄弟元素(-756)操作。兄弟节点大于1在红黑树中对应着兄弟节点存在红子节点
思考六:如果最近的那个节点没有多余元素呢?
答:将父亲节点看成删除的节点循环向上继续寻找,但是过程中将只有一个元素的兄弟节点和父节点合并。若node到了根节点的子节点,判断node兄弟节点(根节点另一个方向)是否有多余元素,若有就会在此时交换值并结束,但是如果仍然没有,此时的兄弟节点就会和根节点结合作为根节点。这样就减小了另一侧整体的层数,也就是通过降低树深度达到平衡的效果。

思考七:思考六中关于234树的操作反应在红黑树上是什么样的?
答:在到跟节点之前,所有兄弟节点的左右子节点为黑色(真黑色或null)的兄弟节点都变成红色(对应在234树中的兄弟和父节点合并),直到找到兄弟节点的子节点存在红色节点。然后根据兄弟为黑色有红节点 情况1—3
思考七图解1:
目标:删除节点1(四十右边的省略)
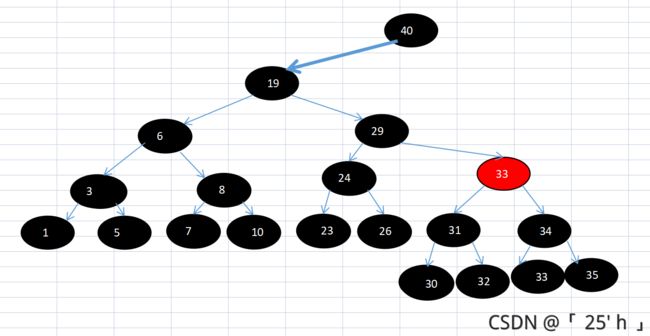
思考七图解2:
因为1的兄弟节点为5,5的左右子节点为空(即为黑色)不满足转化条件,将兄弟节点5变成红色。指针指向上一个元素3。

思考七图解3:
因为3的兄弟节点为8,8的左右子节点为黑色不满足转化条件,将兄弟节点8变成红色。指针指向上一个元素6。

思考七图解4:
因为6的兄弟节点为29,29的左右子节点存在红色,满足转化条件,根据 兄弟为黑色有红色子节点 情况 1—3,进行左旋后换颜色即可。

思考七图解5:
进行左旋后的情况。
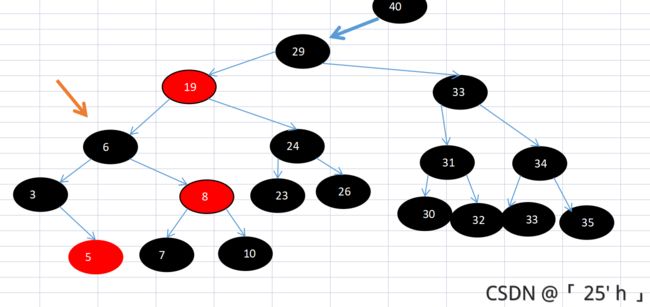
思考七图解6:
换颜色(将旋转节点左右子节点置为黑)。完成,此时就符合黑色平衡
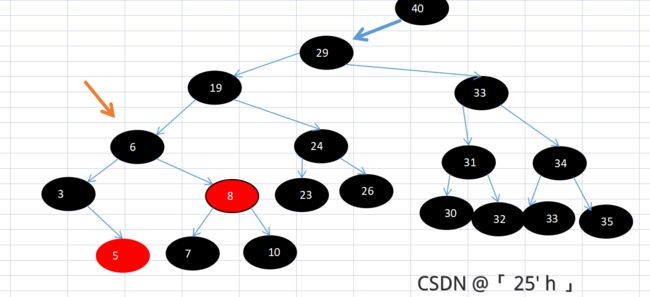
续思考七:要是到达根节点时任然完不成呢?
答:该操作必定在根节点前平衡,别忘了我们变成平衡树的方式有两种:
一就是通过增加黑色节点(思考七的过程)
二是通过下降红黑树的黑色层数 (对应234树的节点层数)
在根节点附近的情况有三种:
1:root根节点的另一个方向的子节点为红色:
和 (假)兄弟为红色 情况 4情况相同
和思考七的过程相同,不过此时的父节点为根节点。在左右旋的时候

2:root根节点的另一个方向的子节点为黑色且该黑色节点子节点存在红色节点:
和 兄弟为黑色有红子节点 情况1—3情况相同

3:root根节点的另一个方向的子节点为黑色且该黑色节点子节点不存在红色节点:
这种情况走正常的程序是不满足的情况,会将8置为红,黄色指针继续向上,指向根节点,此时会强制退出循环。
强制退出它平衡了吗?
答:平衡了,之前根节点7节点左边少一个黑的,这时让8变成红,就在根节点7右边减少了黑的,所以平衡了

代码
代码最简单,但是。。。。理解有难度
//空或者为两黑时进入程序,执行后会直接进入下一次循环
//循环条件node!=root&&getColor(node)==BLACK
if(getColor(leftOf(rBro))==BLACK&&getColor(rightOf(rBro))==BLACK){
setColor(rBro,RED);
node=parentOf(node);
}
思考:父节点红且兄弟无红色子节点
思路
这种情况只要将该红色父节点下两边的树的黑色都减少一层(删除的一侧已经减少,只要将另一侧减少一层黑色),再将该红色父节点变成黑色即可。
该红色父节点变成黑色意味着:在左右的子节点路径上同时增加了一个黑色节点
图解
第一步:该节点兄弟子节点为黑,不满足,将兄弟变红,向上走

第二步:该节点兄弟子节点仍为黑,不满足,将兄弟变红,向上走
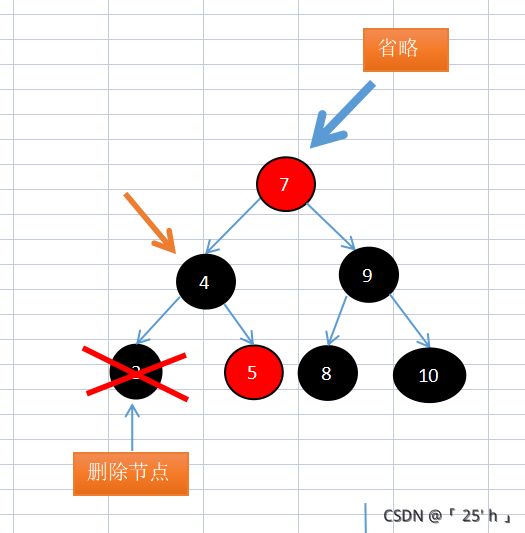
第三步:该节点为红,就直接将该节点变成黑色,就平衡了。
平衡结果:

该过程对应在234树中就是这种情况,不过要注意234树原来的(002,005)节点在红黑树中是005为黑色在上面,002为红色的在下面

fixAfterRemove流程图
整合调整的代码(fixAfterRemove)
private void fixAfterRemove(RBNode node) {
while (node != root && getColor(node) == BLACK) {
//删除节点是父节点的左节点
if (node == leftOf(parentOf(node))) {
RBNode rBro = rightOf(parentOf(node));
//(假)兄弟为红色 情况四
if (getColor(rBro) == RED) {
leftRotate(parentOf(node));
rBro = rightOf(parentOf(node));
}
//兄弟为黑色且无红色节点 情况5
if (getColor(leftOf(rBro)) == BLACK && getColor(rightOf(rBro)) == BLACK) {
setColor(rBro, RED);
node = parentOf(node);
} else {//兄弟为黑色有红色节点 情况1---3
if (getColor(rightOf(rBro)) == BLACK) {
rightRotate(rBro);
rBro = rightOf(parentOf(node));
}
leftRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(rightOf(rBro), BLACK);
break;
}
} else {//删除节点是父节点的右节点
RBNode lBro = leftOf(parentOf(node));
if (getColor(lBro) == RED) {
rightRotate(parentOf(node));
lBro = leftOf(node);
}
if (getColor(rightOf(lBro)) == BLACK && getColor(leftOf(lBro)) == BLACK) {
setColor(lBro, RED);
node = parentOf(node);
} else {//两红或者一红
if (getColor(leftOf(lBro)) == BLACK) {
leftRotate(lBro);
lBro = leftOf(parentOf(node));
}
rightRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(leftOf(lBro), BLACK);
break;
}
}
}
//替代借点为红色,直接变黑,该节点下面必不可能还有节点
setColor(node, BLACK);
}
三种方法整合(remove)
public V remove(K key) {
RBNode node = getNode(key);
if (node == null) {
return null;
}
V oldValue = (V) node.value;
deleteNode(node);
return oldValue;
}
删除代码整合
public V remove(K key) {
RBNode node = getNode(key);
if (node == null) {
return null;
}
V oldValue = (V) node.value;
deleteNode(node);
return oldValue;
}
private RBNode getNode(K key) {
RBNode tail = root;
if (root == null) {
throw new RuntimeException("不可能空");
}
while (tail != null) {
int cmp = key.compareTo((K) tail.key);
if (cmp < 0) {
tail = leftOf(tail);
} else if (cmp > 0) {
tail = rightOf(tail);
} else {
return tail;
}
}
return null;
}
private RBNode deleteNode(RBNode node) {
if (leftOf(node) != null && rightOf(node) != null) {
RBNode pre = pre(node);
node.key = pre.key;
node.value = pre.value;
node = pre;
}
RBNode replace = leftOf(node) != null ? leftOf(node) : rightOf(node);
if (replace != null) {
replace.parent = parentOf(node);
if (parentOf(node) == null) {
root = replace;
} else if (node == leftOf(parentOf(node))) {
node.parent.left = replace;
} else {
node.parent.right = replace;
}
node.left = node.right = node.parent = null;
if (getColor(node) == BLACK) {
fixAfterRemove(replace);
}
}
else {
if (getColor(node) == BLACK) {
fixAfterRemove(node);
}
if (parentOf(node) != null) {
if (node == leftOf(parentOf(node))) {
node.parent.left = null;
} else {
node.parent.right = null;
}
node.parent = null;
} else {
root = null;
}
}
return null;
}
private void fixAfterRemove(RBNode node) {
while (node != root && getColor(node) == BLACK) {
if (node == leftOf(parentOf(node))) {
RBNode rBro = rightOf(parentOf(node));
if (getColor(rBro) == RED) {
leftRotate(parentOf(node));
rBro = rightOf(parentOf(node));
}
if (getColor(leftOf(rBro)) == BLACK && getColor(rightOf(rBro)) == BLACK) {
setColor(rBro, RED);
node = parentOf(node);
} else {
if (getColor(rightOf(rBro)) == BLACK) {
rightRotate(rBro);
rBro = rightOf(parentOf(node));
}
leftRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(rightOf(rBro), BLACK);
break;
}
} else {
RBNode lBro = leftOf(parentOf(node));
if (getColor(lBro) == RED) {
rightRotate(parentOf(node));
lBro = leftOf(node);
}
if (getColor(rightOf(lBro)) == BLACK && getColor(leftOf(lBro)) == BLACK) {
setColor(lBro, RED);
node = parentOf(node);
} else {//两红或者一红
if (getColor(leftOf(lBro)) == BLACK) {
leftRotate(lBro);
lBro = leftOf(parentOf(node));
}
rightRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(leftOf(lBro), BLACK);
break;
}
}
}
setColor(node, BLACK);
}
完整代码和测试
创建TreeMap包
包下有这三个类:
RBTreeTest
TreeOperation
RBTree
前两个是测试类,写好的,不用管,运行类RBTreeTest即可
RBTreeTest
package TreeMap;
import java.util.Scanner;
public class RBTreeTest {
public static void main(String[] args) {
//测试那个打开那个,不能同时打开
// insertOpt(); //新增节点
// deleteOpt(); //删除节点
}
public static void insertOpt(){
Scanner scanner=new Scanner(System.in);
RBTree<String,Object> rbt=new RBTree<>();
while (true){
System.out.println("请输入你要插入的节点:");
String key=scanner.next();
System.out.println();
if(key.length()==1){
key="00"+key;
}else if(key.length()==2){
key="0"+key;
}
rbt.put(key,null);
TreeOperation.show(rbt.getRoot());
}
}
public static void deleteOpt(){
RBTree<String,Object> rbt=new RBTree<>();
rbt.put("001",null);
rbt.put("002",null);
rbt.put("003",null);
rbt.put("004",null);
rbt.put("005",null);
rbt.put("006",null);
rbt.put("007",null);
rbt.put("008",null);
rbt.put("009",null);
rbt.put("010",null);
rbt.put("011",null);
TreeOperation.show(rbt.getRoot());
Scanner scanner=new Scanner(System.in);
while (true){
System.out.println("请输入你要删除的节点:");
String key=scanner.next();
System.out.println();
if(key.length()==1){
key="00"+key;
}else if(key.length()==2){
key="0"+key;
}
rbt.remove(key);
TreeOperation.show(rbt.getRoot());
}
}
}
TreeOperation
package TreeMap;
public class TreeOperation {
public static int getTreeDepth(RBTree.RBNode root) {
return root == null ? 0 : (1 + Math.max(getTreeDepth(root.getLeft()), getTreeDepth(root.getRight())));
}
private static void writeArray(RBTree.RBNode currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
if (currNode == null) return;
if(currNode.isColor()){
res[rowIndex][columnIndex] = ("\033[30;3m" + currNode.getValue()+"\033[0m") ;
}else {
res[rowIndex][columnIndex] = ("\033[31;3m" + currNode.getValue()+"\033[0m") ;
}
int currLevel = ((rowIndex + 1) / 2);
if (currLevel == treeDepth) return;
int gap = treeDepth - currLevel - 1;
if (currNode.getLeft() != null) {
res[rowIndex + 1][columnIndex - gap] = "/";
writeArray(currNode.getLeft(), rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
}
if (currNode.getRight() != null) {
res[rowIndex + 1][columnIndex + gap] = "\\";
writeArray(currNode.getRight(), rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
}
}
public static void show(RBTree.RBNode root) {
if (root == null) {
System.out.println("EMPTY!");
System.exit(0);
}
int treeDepth = getTreeDepth(root);
int arrayHeight = treeDepth * 2 - 1;
int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
String[][] res = new String[arrayHeight][arrayWidth];
for (int i = 0; i < arrayHeight; i ++) {
for (int j = 0; j < arrayWidth; j ++) {
res[i][j] = " ";
}
}
writeArray(root, 0, arrayWidth/2, res, treeDepth);
for (String[] line: res) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < line.length; i ++) {
sb.append(line[i]);
if (line[i].length() > 1 && i <= line.length - 1) {
i += line[i].length() > 4 ? 2: line[i].length() - 1;
}
}
System.out.println(sb.toString());
}
}
}
RBTree
package TreeMap;
public class RBTree<K extends Comparable<K>,V>{
private RBNode root;
private static final boolean BLACK=true;
private static final boolean RED=false;
public void put(K key,V value){
if(null == root){
root=new RBNode<>(key,value==null?key:value,null);
return;
}
int com;
RBNode tail=root;
RBNode parentTail;
if(key==null){
throw new RuntimeException("空指针异常");
}
do{
parentTail=tail;
com=key.compareTo((K) tail.key);
if(com<0){
tail=leftOf(tail);
}else if (com>0){
tail=rightOf(tail);
}else {
tail.value=value==null?key:value;
return;
}
}while (tail!=null);
RBNode newRBNode=new RBNode<>(key,value==null?key:value,parentTail);
if (com<0){
parentTail.left=newRBNode;
}else {
parentTail.right=newRBNode;
}
fixAfterPut(newRBNode);
}
private void fixAfterPut(RBNode newRBNode) {
setColor(newRBNode,RED);
while (newRBNode != root&&getColor(parentOf(newRBNode))==RED){
RBNode grandFather=parentOf(parentOf(newRBNode));
RBNode father=parentOf(newRBNode);
if(leftOf(grandFather)==father){
RBNode uncle=rightOf(grandFather);
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(rightOf(father)==newRBNode){
leftRotate(father);
newRBNode=father;
}
rightRotate(grandFather);
}
}else {
RBNode uncle=leftOf(grandFather);
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(leftOf(father)==newRBNode){
rightRotate(father);
newRBNode=father;
}
leftRotate(grandFather);
}
}
}
setColor(root,BLACK);
}
public V remove(K key) {
RBNode node = getNode(key);
if (node == null) {
return null;
}
V oldValue = (V) node.value;
deleteNode(node);
return oldValue;
}
//获取该节点
private RBNode getNode(K key) {
RBNode tail = root;
if (root == null) {
throw new RuntimeException("不可能空");
}
while (tail != null) {
int cmp = key.compareTo((K) tail.key);
if (cmp < 0) {
tail = leftOf(tail);
} else if (cmp > 0) {
tail = rightOf(tail);
} else {
return tail;
}
}
return null;
}
private RBNode deleteNode(RBNode node) {
if (leftOf(node) != null && rightOf(node) != null) {
RBNode pre = pre(node);
node.key = pre.key;
node.value = pre.value;
node = pre;
}
RBNode replace = leftOf(node) != null ? leftOf(node) : rightOf(node);
if (replace != null) {
replace.parent = parentOf(node);
if (parentOf(node) == null) {
root = replace;
} else if (node == leftOf(parentOf(node))) {
node.parent.left = replace;
} else {
node.parent.right = replace;
}
node.left = node.right = node.parent = null;
if (getColor(node) == BLACK) {
fixAfterRemove(replace);
}
}
else {
if (getColor(node) == BLACK) {
fixAfterRemove(node);
}
if (parentOf(node) != null) {
if (node == leftOf(parentOf(node))) {
node.parent.left = null;
} else {
node.parent.right = null;
}
node.parent = null;
} else {
root = null;
}
}
return null;
}
private void fixAfterRemove(RBNode node) {
while (node != root && getColor(node) == BLACK) {
if (node == leftOf(parentOf(node))) {
RBNode rBro = rightOf(parentOf(node));
if (getColor(rBro) == RED) {
leftRotate(parentOf(node));
rBro = rightOf(parentOf(node));
}
if (getColor(leftOf(rBro)) == BLACK && getColor(rightOf(rBro)) == BLACK) {
setColor(rBro, RED);
node = parentOf(node);
} else {
if (getColor(rightOf(rBro)) == BLACK) {
rightRotate(rBro);
rBro = rightOf(parentOf(node));
}
leftRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(rightOf(rBro), BLACK);
break;
}
} else {
RBNode lBro = leftOf(parentOf(node));
if (getColor(lBro) == RED) {
rightRotate(parentOf(node));
lBro = leftOf(node);
}
if (getColor(rightOf(lBro)) == BLACK && getColor(leftOf(lBro)) == BLACK) {
setColor(lBro, RED);
node = parentOf(node);
} else {
if (getColor(leftOf(lBro)) == BLACK) {
leftRotate(lBro);
lBro = leftOf(parentOf(node));
}
rightRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(leftOf(lBro), BLACK);
break;
}
}
}
setColor(node, BLACK);
}
//前驱
private RBNode pre(RBNode node) {
RBNode l = leftOf(node);
while (l.right != null) {
l = l.right;
}
return l;
}
//后继
private RBNode suc(RBNode node){
RBNode r=node.right;
while (r.left!=null){
r=r.left;
}
return r;
}
private void leftRotate(RBNode p) {
if(p!=null){
RBNode l=p.right;
setColor(l, p.color);
setColor(p, RED);
p.right = l.left;
if (l.left != null) {
l.left.parent = p;
}
l.parent = p.parent;
if (p.parent == null) {
root = l;
} else if (p.parent.left == p) {
p.parent.left = l;
} else {
p.parent.right = l;
}
l.left = p;
p.parent = l;
}
}
private void rightRotate(RBNode p) {
RBNode r = p.left;
setColor(r, getColor(p));
setColor(p, RED);
p.left = r.right;
if (r.right != null) {
r.right.parent = p;
}
r.parent = p.parent;
if (p.parent == null) {
root = r;
} else if (p.parent.left == p) {
p.parent.left = r;
} else {
p.parent.right = r;
}
r.right = p;
p.parent = r;
}
private static boolean getColor(RBNode rbNode){
return rbNode==null?BLACK:rbNode.color;
}
private static void setColor(RBNode rbNode, boolean b){
if(rbNode!=null){
rbNode.color=b;
}
}
private static RBNode parentOf(RBNode rbNode){
return rbNode==null?null:rbNode.parent;
}
private static RBNode leftOf(RBNode rbNode){
return rbNode==null?null:rbNode.left;
}
private static RBNode rightOf(RBNode rbNode){
return rbNode==null?null:rbNode.right;
}
public void show(){
if(root==null){
System.out.println("空");
}else {
show(root);
}
}
private void show(RBNode tail){
if (tail.left!=null){
show(tail.left);
}
System.out.println(tail);
if (rightOf(tail)!=null){
show(rightOf(tail));
}
}
public RBNode getRoot() {
return root;
}
static class RBNode<K extends Comparable<K>,V>{
K key;
V value;
private boolean color;
RBNode parent;
RBNode left;
RBNode right;
public RBNode(K key, V value, RBNode parent) {
this.key = key;
this.value = value;
this.color = BLACK;
this.parent = parent;
}
@Override
public String toString() {
return "RBNode{" +
"key=" + key +
", value=" + value +
", color=" + (color?"BLACK":"RED") +
'}';
}
public RBNode getLeft() {
return left;
}
public RBNode getRight() {
return right;
}
public boolean isColor() {
return color;
}
public V getValue() {
return value;
}
}
}