数据结构中的七大排序(Java实现)
目录
一、直接插入排序
二、希尔排序
三、直接选择排序
四、堆排序
五、冒泡排序
六、快速排序
七、归并排序
一、直接插入排序
思想:
定义i下标之前的元素全部已经有序,遍历一遍要排序的数组,把i下标前的元素全部进行排序,当遍历玩这个数组后,就已经排好序了。
代码如下:
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i - 1;
for(; j >= 0;; j--) {
if(array[j] > tmp) {
array[j + 1] = array[j];
} else {
break;
}
}
array[j + 1] = tmp;
}
}代码解析
要使i下标之前的元素都有序,定义一个j下标,为i - 1;再用tmp记录i下标的位置,只要j下标元素比tmp大,j下标的元素就要放到j+1下标,最后j走完后,再把最小的tmp放在j+1位置。
时间复杂度、空间复杂度、稳定性:
时间:O(n^2)
空间:O(1)
稳定性:稳定
二、希尔排序
思想:
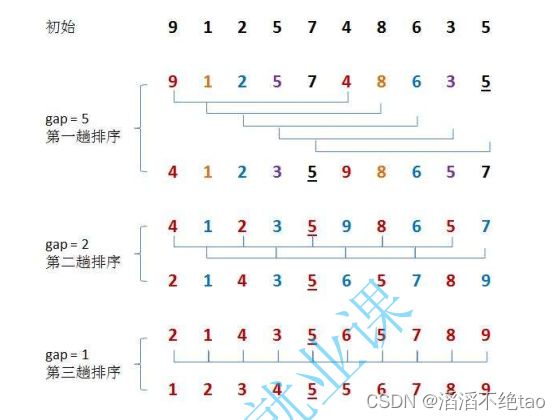
希尔排序也称缩小增量排序,就是分次去进行排序,越排到后面就会越有序,每次间隔是gap,然后逐渐缩小,到最后间隔为0,也就是用我们的直接插入排序,数组越有序,速度也会越快。那么就很简单了,我们只需改一下直接插入排序每次排序的间隔,把他们分成不同组进行排序,直到最后间隔为0,就只剩一组,然后也是用直接插入排序,做最后一次排序,排完就是有序的了。
图式例:
代码如下:
public static void shellSort(int[] array) {
int gap = array.length / 2;
while (gap >= 1) {
gap /= 2;
shell(array, gap);
}
}
public static void shell(int[] array, int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i - gap;
for(; j >= 0; j -= gap) {
if(array[j] > tmp) {
array[j + gap] = array[j];
} else {
break;
}
}
array[j + gap] = tmp;
}
}时间复杂度、空间复杂度、稳定性:
时间:n^1.3(严蔚敏) 因为gap取值方式不同,计算出来的时间复杂度也会不同
空间:O(1)
稳定性:不稳定
三、直接选择排序
思想:
直接选择排序也是和直接插入排序差不多,定义i下标前的元素全部都有序,不过排序的方式不同,它是拿i下标前的元素和i下标后的元素进行比较,找到下标最小的元素,把最小元素放进i下标中,同时这个i下标元素放到被这个最小下标位置。
代码实现:
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;//记录最小值的下标
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[minIndex]) {
minIndex = j;
}
}
//走完这里,找到最小元素的下标minIndex
//交换
int tmp = array[i];
array[i] = array[minIndex];
array[minIndex] = tmp;
}
}时间复杂度、空间复杂度、稳定性:
时间:O(n^2)
空间:O(1)
稳定性:不稳定
四、堆排序
思想:
堆其实就是完全二叉树,下标是从上到下,从左到右依次递增,要把堆排序成升序,就要把他先变成大根堆,每次出大根堆的顶点,把顶点放在最后一个节点,然后再向下调整一次,第二次把大根堆的顶点放到倒数第二个位置,依次往后推。
代码实现:
//堆排序
public static void heapSort(int[] array) {
//先转换成大根堆
createHeap(array);
//开始换,然后向下转换
for (int i = array.length - 1; i > 0 ; i--) {
//i下标的节点和堆顶交换
int tmp = array[0];
array[0] = array[i];
array[i] = tmp;
//向下调整
siftDown(array,0, i);
}
}
//创建大根堆
public static void createHeap(int[] array) {
//从最后一个父节点开始向下调整,下标依次往前减
//parent = (child - 1) / 2; 左:child = parent * 2 + 1 右:child = parent * 2 + 2
for (int i = (array.length - 1 - 1) / 2; i >= 0 ; i--) {
siftDown(array, i, array.length);
}
}
//向下调整
public static void siftDown(int[] array, int parent, int length) {
//定义一个child为该父节点的左孩子
int child = parent * 2 + 1;
while (child < length) {
//比较改父节点的左右孩子,把值最大的孩子作为交换节点
if(array[child] < array[child + 1]) {
child += 1;
}
//比较父节点和孩子节点大小
if(array[parent] < array[child]) {
//交换
int tmp = array[parent];
array[parent] = array[child];
array[child] = tmp;
parent = child;
child = child * 2 + 1;
} else {
break;
}
}
}
时间复杂度、空间复杂度、稳定性:
时间复杂度:O(NlogN)
空间复杂度:O(1)
稳定性:不稳定
五、冒泡排序
思想:
冒泡排序的思想很简单,就是第一次把最大的值放到数组最后一个下标中,再把第二大的元素放到数组倒数第二个下标中,依次类推
代码实现:
//冒泡排序
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length; i++) {
boolean flag = false;//标记
for (int j = 0; j < array.length - 1 - i; j++) {
if(array[j] > array[j + 1]) {
//交换
int tmp =array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
flag = true;
}
}
if(!flag) {
break;
}
}
}时间复杂度、空间复杂度、稳定性:
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
六、快速排序
思想:
使用递归思想(也可以采用非递归思想),把一组数据划分成两部分,左边都小于该下标元素,右边都大于该下标元素,再在左边去找元素划分,右边元素去划分,依次往后推,直到左右两边都没有元素可以划分了,就是只剩一个元素了,这时候往回倒,就有序了
代码实现:
public static void quickSort(int[] array) {
int left = 0;
int right = array.length - 1;
quick(array, left, right);
}
public static void quick(int[] array, int start, int end) {
//递归结束条件
if(start >= end) {
return;
}
int pivot = partition(array, start, end);
quick(array, start, pivot - 1);
quick(array, pivot + 1, end);
}
public static int partition(int[] array, int left, int right) {
//找到一个下标元素,左边都比这个下标元素小,右边都比这个下标元素大,并且还要返回这个下标
//记录下标为0的值,放在tmp中
int tmp = array[0];
while (left < right) {
//先走右边
if(left < right && array[right] >= tmp) {
right--;
}
if(left < right && array[left] <= tmp) {
left++;
}
//左下标的值大于tmp,右下标的值小于tmp,这两个下标值交换
int newTmp = array[left];
array[left] = array[right];
array[right] = newTmp;
}
//走到这,left和right相遇了,left下标的值和tmp交换,并且返回这个位置的下标
int newTmp = tmp;
tmp = array[left];
array[left] = newTmp;
return left;
}
时间复杂度、空间复杂度、稳定性:
时间复杂度:O(NlogN)
空间复杂度:O(logN~N)
稳定性:不稳定
七、归并排序
思想:
将一组数组分割成左右两部分,和快速排序找出的中件位置不同,归并的中间位置是最左和最右下标相加再除2(left+right)/ 2,运用的也是递归思想(也可以采用非递归思想),采用分治法,一直找到最左边进行排序,然后再找最右边进行排序,再往归回整体排序(合并),合并的时候是放在一个临时数组中,再把这个临时数组拷贝到原数组,下标要对应
代码实现:
public static void mergeSort(int[] array) {
int start = 0;
int end = array.length - 1;
mergeSortFunc(array, start, end);
}
//套壳
public static void mergeSortFunc(int[] array, int start, int end) {
//递归结束标志
if(start >= end) {
return;
}
//求出中间节点位置
int mid = (start + end) / 2;
//左边
mergeSortFunc(array, start, mid);
//右边
mergeSortFunc(array, mid + 1, end);
//合并
merge(array, start, mid, end);
}
//合并
public static void merge(int[] array, int left, int mid, int right) {
//定义mid两边的左右下标
int s1 = left;
int e1 = mid;
int s2 = mid + 1;
int e2 = right;
//定义一个新的数组,存放array排序完后的数组
int[] tmpArray = new int[right - left - 1];
int k = 0;
while (s1 <= e1 && s2 <= e2) {
//比较左右两边s1和s2的值
if(array[s1] < array[s2]) {
tmpArray[k++] = array[s1++];
} else {
tmpArray[k++] = array[s2]++;
}
if(s1 <= e1) {
tmpArray[k++] = array[s1++];
}
if(s2 <= e2) {
tmpArray[k++] = array[s2++];
}
}
//拷贝到原数组
for (int i = 0; i < tmpArray.length; i++) {
array[left + i] = tmpArray[i];
}
}时间复杂度、空间复杂度、稳定性:
时间复杂度:O(NlogN)
空间复杂度:O(N)
稳定性:不稳定
都看到这了,给个免费的赞呗,谢谢谢谢!!!