LeetCode 221. 最大正方形(C++) 动态规划

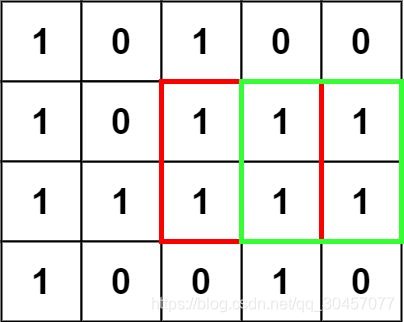
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

 输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 ‘0’ 或 ‘1’

动态规划

可以使用动态规划降低时间复杂度。我们用 dp(i,j) 表示以 (i, j) 为右下角，且只包含 1 的正方形的边长最大值。如果我们能计算出所有 dp(i, j)的值，那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值，其平方即为最大正方形的面积。

那么如何计算 dp 中的每个元素值呢？对于每个位置 (i, j)，检查在矩阵中该位置的值：

如果该位置的值是 0，则 dp(i, j) = 0，因为当前位置不可能在由 1 组成的正方形中；
如果该位置的值是 1，则 dp(i, j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值加 1，状态转移方程如下：
dp(i, j)=min(dp(i−1, j), dp(i−1, j−1), dp(i, j−1))+1

如果读者对这个状态转移方程感到不解，可以参考 1277. 统计全为 1 的正方形子矩阵的官方题解，其中给出了详细的证明。
此外，还需要考虑边界条件。如果 i 和 j 中至少有一个为 0，则以位置 (i, j)为右下角的最大正方形的边长只能是 1，因此 dp(i, j) = 1。
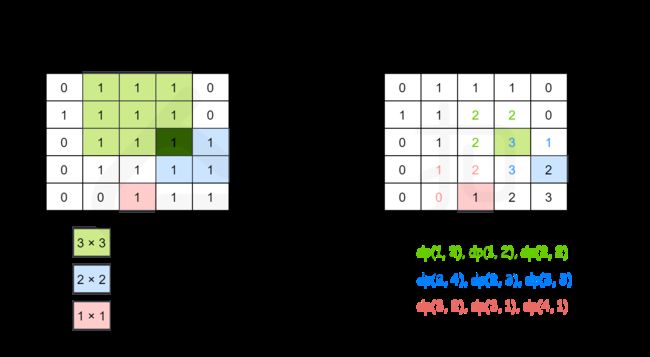
以下用一个例子具体说明。原始矩阵如下。

0 1 1 1 0
1 1 1 1 0
0 1 1 1 1
0 1 1 1 1
0 0 1 1 1

对应的 dp 值如下。

0 1 1 1 0
1 1 2 2 0
0 1 2 3 1
0 1 2 3 2
0 0 1 2 3

下图也给出了计算dp 值的过程。

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
    //矩阵行数为零 or 矩阵只有一行  且第一行尺寸为零
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return 0;
        }
        int maxSide = 0;
        int rows = matrix.size(), columns = matrix[0].size();
        vector<vector<int>> dp(rows, vector<int>(columns));
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {//边界条件
                        dp[i][j] = 1;
                    } else {
                    //状态转移方程
                        dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                    //更新最大边长度
                    maxSide = max(maxSide, dp[i][j]);
                }
            }
        }
        //面积
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
};

复杂度分析

时间复杂度：O(mn) ，其中 m 和 n 是矩阵的行数和列数。需要遍历原始矩阵中的每个元素计算dp 的值。
空间复杂度：O(mn)，其中 m 和 n 是矩阵的行数和列数。创建了一个和原始矩阵大小相同的矩阵dp。由于状态转移方程中的dp(i, j)由其上方、左方和左上方的三个相邻位置的 dp 值决定，因此可以使用两个一维数组进行状态转移，空间复杂度优化至 O(n)。