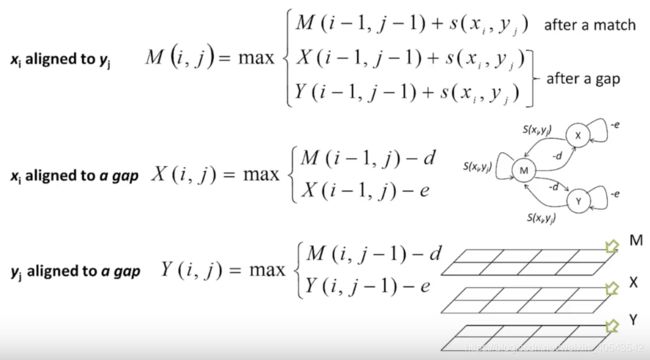序列比对算法

Pairwise Sequence Alignment 双序列比对
给定两个序列，判断其相似性。相似的序列可能有相似的结构，从而有相似的功能。不同物种中相似的序列，往往可能有相似的祖先。

1 序列比对中的基本概念

先看一个在线工具：

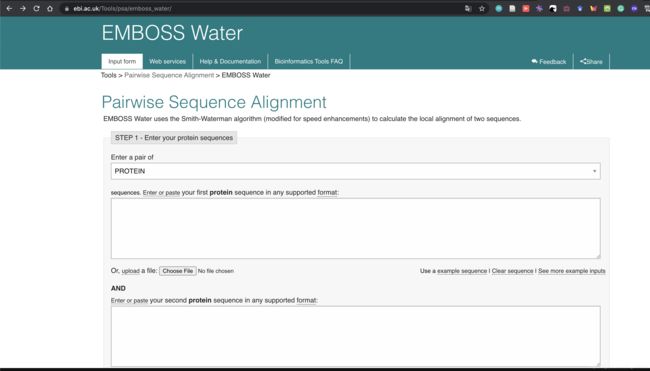
结果：

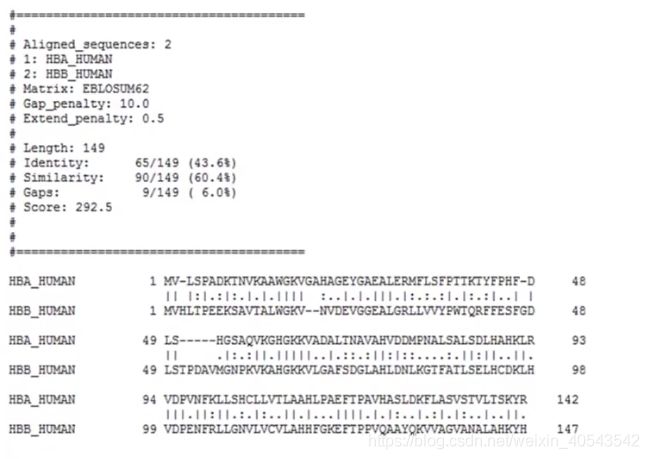
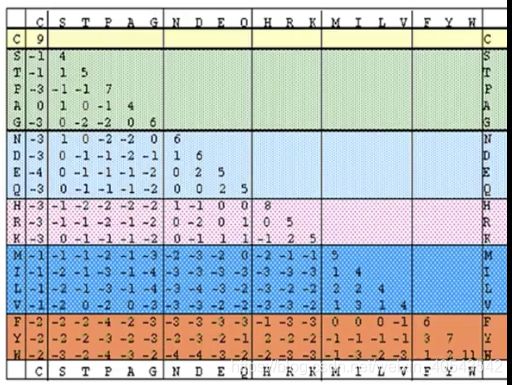
“｜”代表相同的残基，“ : ”和“ . ”代表残基的相似程度，“ : ”表示比较相似（大于0），“ . ”表示不太相似（小于0），根据一个替换矩阵来衡量（对称、上下游无关），根据矩阵进行罚分。空位是gap( = insertion or deletion, indel)，因为indel通常会对序列的功能产生影响，所以空位在比对中总是对应负分（空位罚分）。由于插入和删除往往涉及多个残基，所以空位罚分采用线性组合的形式：
Affine gap penalty: opening a gap receives a penalty of d; extending a gap receives a penalty of e. The total penalty for a gap with length n would be:
$$Penalty=d+(n-1)\times e$$
例如：
Gap penalty: 10.0
Extend penalty: 0.5
则上图第二个gap罚分为 $10+(2-1)\times 0.5=10.5$
最后一个gap罚分为 $10+(5-1)\times 0.5=12$
最后将所有罚分加起来，得到总分数：$292.5$

2 利用动态规划进行全局比对

输入数据：两条序列S1和S2
参数：打分函数 scoring function $f$
输出：可使分数最大化的比对结果
$$\underset{ali}{\mathrm{argmax}}(f(ali(S1,S2)))$$

2.1 枚举法（Enumerate）?

两条长度相同的序列，新的比对结果能且只能通过插入空位产生，最极端的情况就是所有残基都对应空位，这时比对结果的序列长度就是2倍的序列长度，因此所有可能比对结果数目是从2n中选取n个的可能数目：
$$\left(\begin{array}{c}2n\\ n\end{array}\right)=\frac{(2n)}{(n!{)}^2}$$
若序列长度为300，
$$\left(\begin{array}{c}2n\\ n\end{array}\right)=\frac{(2n)!}{(n!{)}^2}=\frac{(2\ast 300)!}{(300!{)}^2}\approx 7\times 10^{88}$$
这个数目约等于目前可见宇宙中所有粒子数目的一亿倍！

可见，枚举法在实践中并不可行。

2.2 动态规划法(Needleman-Wunsch algorithm)

一个残基可能的情况：

• 比对到另一个残基
• 比对到空位

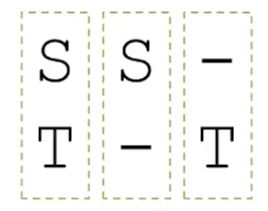
The best alignment that ends at a given pair of symbols is the best alignment of the sequences up to that point, plus the best alignment for the two additional symbols.
最好的比对就是之前最好的比对加上当前位置最好的比对。

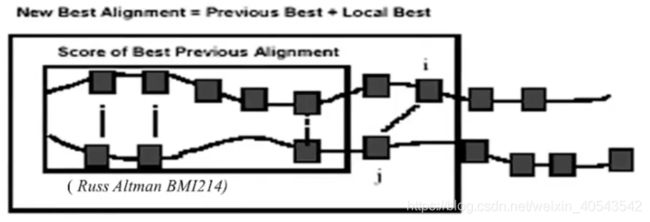
动态规划是一种用来解决具有最优子结构性质的优化问题的计算机算法。局部最优解的组合就是全局最优解。

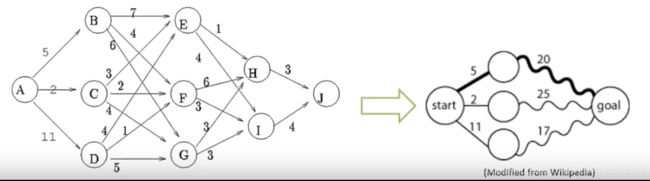
1. Break the problem into smaller sub-problems.
2. Solve these sub-problems optimally recursively.
3. Use these optimal solutions to construct an optimal solution for the original problem.

Sequence alignment with Dynamic Programming: the Formula

• Align two sequence: x and y
  • $F(i,j)$ 是$x_{1...i}$ 和$y_{1...j}$最好比对的打分。
  • $s(A,B)$是A, B的打分；$d$是空位罚分

$$\begin{array}{l}F(0,0)=0\\ F(i,j)=\max \{\begin{array}{l}F(i-1,j-1)+s\left(x_i,y_j\right)，x_i对应y_j\\ F(i-1,j)+d，x_i对应空位\\ F(i,j-1)+d，y_j对应空位\end{array}\end{array}$$
为了便于理解，将x,y两条序列摆在矩阵的两条边上（动态规划矩阵）：

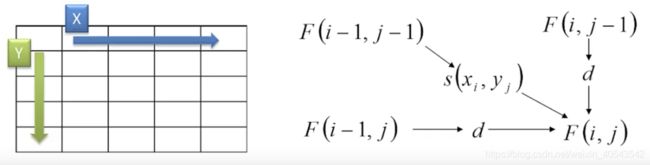
举例：
对于核酸序列

现在将两条序列按照行和列填入到动态规划矩阵中：

首先填最靠边的两排：
因为空位罚分是-5分

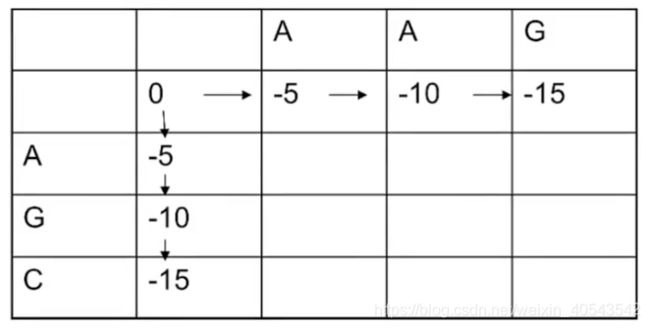
接下来填中间的格子：

我们先看第二行第二列的可能值，有三个：

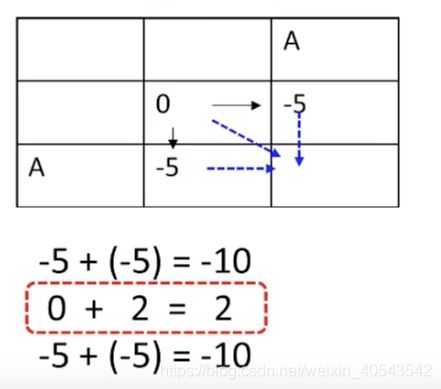
所以这个格子应取最大值2，并画一个反向箭头表明其来源：

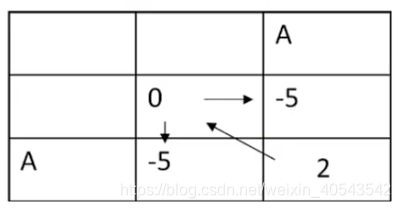
再看下图画圈的“-3”，有两个箭头指向它，代表这两条路径都可以得到-3这个值

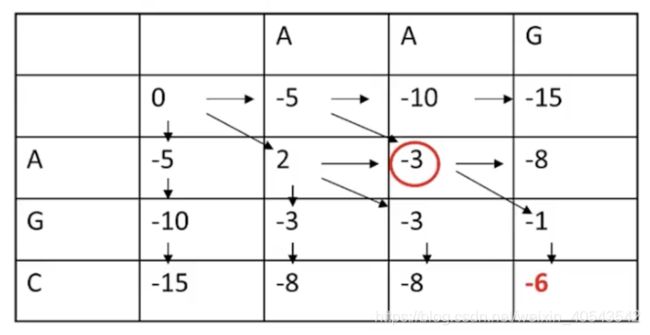
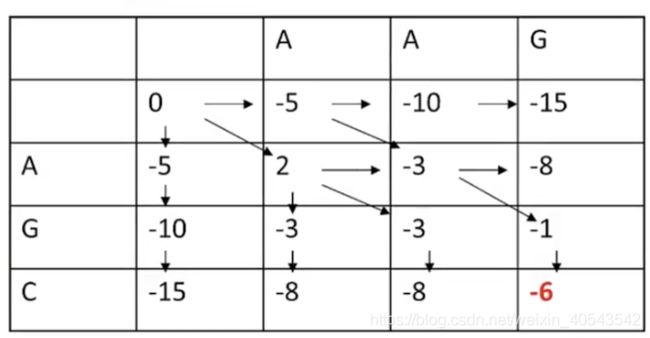
下图“-6”代表最终迭代的最优打分为-6

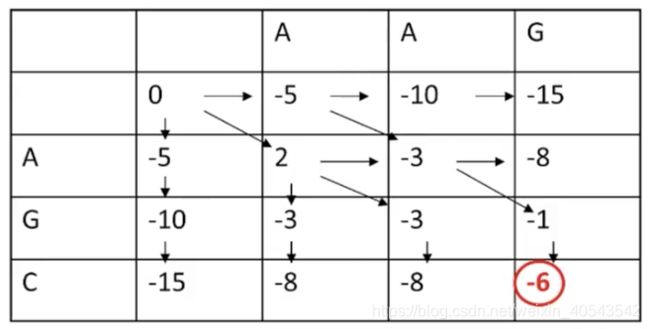
现在，迭代做完了，需要从最后一个值“-6”向前回溯，得到最终的比对：

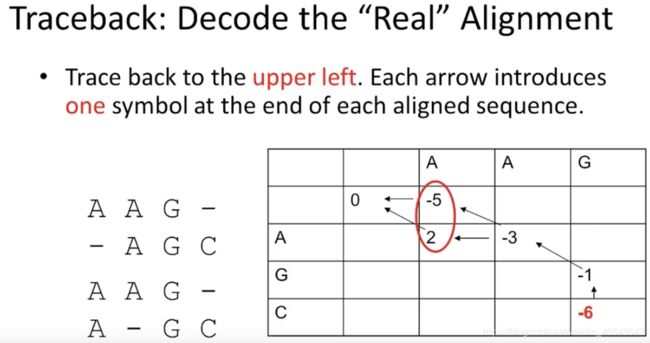
我们想要得到最好的比对结果，在同一个打分规则下，得到相同打分两个比对结果，都是最好的比对。

2.3 考虑仿射空位罚分

即将gap opening和gap extending分开来考虑
$$Penalty=d+(n-1)\times e$$
一对残基之间可能的比对关系有三种：

M代表两个残基对上，不一定相等；X表示x序列有一个插入或者对应y上一个空位；Y表示y序列有一个插入或者对应x上一个空位。
利用计算机中有限状态机的概念，将序列之间的比对描述为在不同状态下的转移。

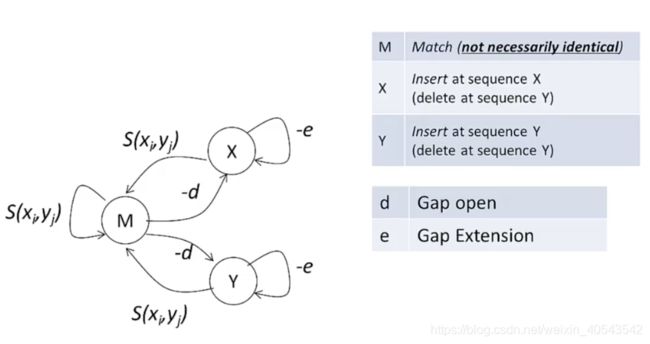
3. 从全局比对到局部比对

上一部分是对两条序列全部进行比对，也就是全局比对（Global Alignment），虽然这个算法得到了广泛地应用，但也存在一些问题。

首先，随着越来越多蛋白质序列的被测定，研究人员发现功能相关的蛋白之间虽然可能在整体蛋白序列上相差甚远，却常常具有相同的功能域，这些片段能够独立的发挥生物学功能，在不同蛋白之间相当保守，但仅靠全局比对算法显然是无法发现这些片段的。另一方面，内含子的发现使得在做核酸水平的序列比对时必须要能正确处理内含子导致的大片段的差异。因此，我们需要方法去发现相似的局部序列。

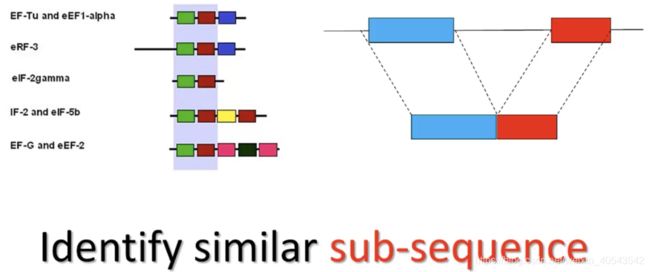
序列局部比对算法（Sequence Local Alignment, Smith-Waterman Algorithm）
$$\begin{array}{l}F(0,0)=0\\ F(i,j)=\max \{\begin{array}{l}F(i-1,j-1)+s\left(x_i,y_j\right)\\ F(i-1,j)+d\\ F(i,j-1)+d\\ 0\end{array}\end{array}$$
跟全局算法比，局部比对算法增加了一个下限0，限制了最低的分数。

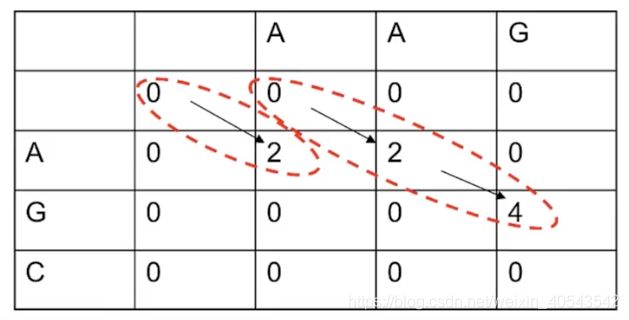
所有的回溯都是局部的，获得的比对也是局部的：

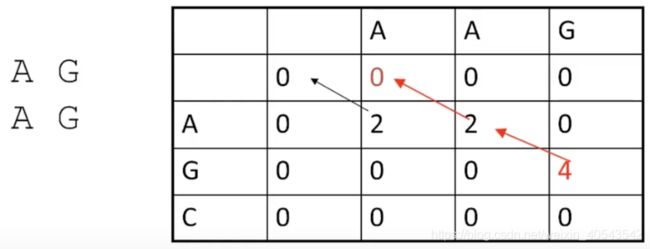
Smith-Waterman算法提高了差异扩大之后，重启比对的能力，从而可以有效地发现局部水平上的相似性，也说明了动态规划算法的灵活性。