算法刷题打卡第47天：排序数组---归并排序

排序数组

难度：中等

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

归并排序

算法简介：
对于给定的一组数据，利用递归与分治技术将数据序列划分成为越来越小的半子表，在对半子表排序后，再用递归方法将排好序的半子表合并成为越来越大的有序序列。

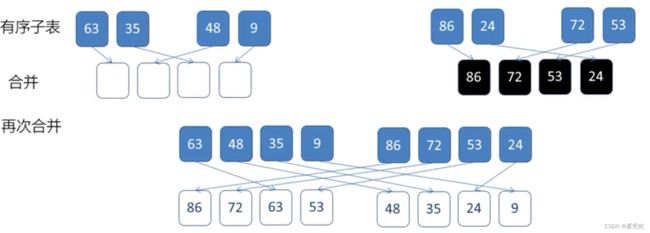
归并排序（降序）图示:

思路：
将长度为n的数组拆为n/2长度的数组，分别对各自进行排序。再将n/2长度的数组使用归并排序，直到最终的排序的数组长度为2，最后将最终排序的数组依次向上合并。

归并排序（升序）过程演示：

补充：

• 为了提升性能，有时我们在半子表的个数小于某个数(比如15)的情况下，对半子表的排序采用其他排序算法，比如插入排序。
• 若将两个有序表合并成一个有序表，称为2-路归并，与之对应的还有多路归并

时间复杂度： $O(nlogn)$，由于归并排序每次都将当前待排序的序列折半成两个子序列递归调用，然后再合并两个有序的子序列，而每次合并两个有序的子序列需要 $O(n)$ 的时间复杂度，所以我们可以列出归并排序运行时间 $T(n)$ 的递归表达式：
$$T(n)=2T(\frac{n}{2})+O(n)$$ 根据主定理我们可以得出归并排序的时间复杂度为 $O(n\log n)$。

空间复杂度： $O(n)$，归并的空间复杂度临时的数组和递归时压入栈的数据占用的空间：$O(n)+O(logn)$，所以空间复杂度最终为 $O(n)$。

代码实现一： 只使用归并排序，递归结束条件为长度小于2，返回当前拆分数组

class Solution:
	# 两个有序子数组合并为一个有序数组
    def merge(self, left, right):        
        left_len, right_len = len(left), len(right)
        l, r = 0, 0
        subnums = []
        while l < left_len and r < right_len:
            if left[l] < right[r]:
                subnums.append(left[l])
                l += 1
            else:
                subnums.append(right[r])
                r += 1
        if l == left_len:
            subnums += right[r:]
        if r == right_len:
            subnums += left[l:]
        return subnums
        
	# 归并排序
    def sortArray(self, nums: List[int]) -> List[int]:
        length = len(nums)
        # 递归结束条件，当长度小于2，直接返回数组
        if length < 2:
            return nums
        left, right = nums[:int(length/2)], nums[int(length/2):]
        return self.merge(self.sortArray(left), self.sortArray(right))

代码实现二： 使用归并排序+插入排序，递归结束条件为长度小于22（据统计，插入排序在长度小于22的数组表现较佳，且归并排序如果长度较小仍需多次递归拆分，相比插入排序速度较慢），返回插入排序后的拆分数组。

class Solution:
	# 两个有序子数组合并为一个有序数组
    def merge(self, left, right):        
        left_len, right_len = len(left), len(right)
        l, r = 0, 0
        subnums = []
        while l < left_len and r < right_len:
            if left[l] < right[r]:
                subnums.append(left[l])
                l += 1
            else:
                subnums.append(right[r])
                r += 1
        if l == left_len:
            subnums += right[r:]
        if r == right_len:
            subnums += left[l:]
        return subnums
	
	# 插入排序
    def insertSort(self, nums, length):
        for i in range(1, length):
            index, value = i, nums[i]
            while index != 0 and value < nums[index-1]:
                nums[index] = nums[index-1]
                index -= 1
            nums[index] = value
        return nums

	# 归并排序
    def sortArray(self, nums: List[int]) -> List[int]:
        length = len(nums)
        # 递归结束条件，当长度小于22，返回插入排序后的数组
        if length < 22:
            return self.insertSort(nums, length)
        left, right = nums[:int(length/2)], nums[int(length/2):]
        return self.merge(self.sortArray(left), self.sortArray(right))

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/sort-an-array