极客时间-数据结构与算法之美(三)
15 | 二分查找(上):如何用最省内存的方式实现快速查找功能?
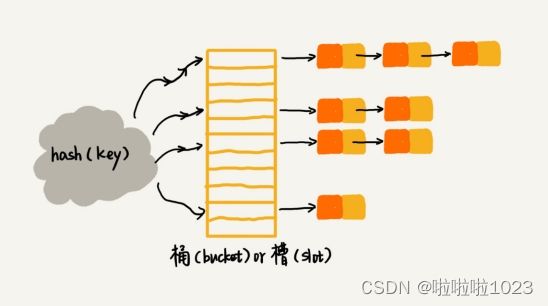
无处不在的二分思想
二分查找针对的是一个有序的数据集合,查找思想有点类似分治思想。每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0。
时间复杂度就是 O(logn)。
二分查找的递归与非递归实现
最简单的情况就是有序数组中不存在重复元素,我们在其中用二分查找值等于给定值的数据。
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (a[mid] == value) {
return mid;
} else if (a[mid] < value) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return -1;
}1. 循环退出条件
注意是 low<=high,而不是 low 2.mid 的取值 实际上,mid=(low+high)/2 这种写法是有问题的。因为如果 low 和 high 比较大的话,两者之和就有可能会溢出。改进的方法是将 mid 的计算方式写成 low+(high-low)/2。更进一步,如果要将性能优化到极致的话,我们可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1)。因为相比除法运算来说,计算机处理位运算要快得多。 3.low 和 high 的更新 low=mid+1,high=mid-1。注意这里的 +1 和 -1,如果直接写成 low=mid 或者 high=mid,就可能会发生死循环。比如,当 high=3,low=3 时,如果 a[3] 不等于 value,就会导致一直循环不退出。 实际上,二分查找除了用循环来实现,还可以用递归来实现。 二分查找应用场景的局限性 首先,二分查找依赖的是顺序表结构,简单点说就是数组。 那二分查找能否依赖其他数据结构呢?比如链表。答案是不可以的,主要原因是二分查找算法需要按照下标随机访问元素。数组按照下标随机访问数据的时间复杂度是 O(1),而链表随机访问的时间复杂度是 O(n)。所以,如果数据使用链表存储,二分查找的时间复杂就会变得很高。 二分查找只能用在数据是通过顺序表来存储的数据结构上。如果你的数据是通过其他数据结构存储的,则无法应用二分查找。 其次,二分查找针对的是有序数据。 如果数据没有序,我们需要先排序。排序的时间复杂度最低是 O(nlogn)。所以,如果我们针对的是一组静态的数据,没有频繁地插入、删除,我们可以进行一次排序,多次二分查找。这样排序的成本可被均摊,二分查找的边际成本就会比较低。 但是,如果我们的数据集合有频繁的插入和删除操作,要想用二分查找,要么每次插入、删除操作之后保证数据仍然有序,要么在每次二分查找之前都先进行排序。针对这种动态数据集合,无论哪种方法,维护有序的成本都是很高的。 所以,二分查找只能用在插入、删除操作不频繁,一次排序多次查找的场景中。针对动态变化的数据集合,二分查找将不再适用。 再次,数据量太小不适合二分查找。 如果要处理的数据量很小,完全没有必要用二分查找,顺序遍历就足够了。 如果数据之间的比较操作非常耗时,不管数据量大小,我都推荐使用二分查找。 最后,数据量太大也不适合二分查找。 二分查找的底层需要依赖数组这种数据结构,而数组为了支持随机访问的特性,要求内存空间连续,对内存的要求比较苛刻。比如,我们有 1GB 大小的数据,如果希望用数组来存储,那就需要 1GB 的连续内存空间。而我们的二分查找是作用在数组这种数据结构之上的,所以太大的数据用数组存储就比较吃力了,也就不能用二分查找了。 二分查找虽然性能比较优秀,但应用场景也比较有限。底层必须依赖数组,并且还要求数据是有序的。对于较小规模的数据查找,我们直接使用顺序遍历就可以了,二分查找的优势并不明显。二分查找更适合处理静态数据,也就是没有频繁的数据插入、删除操作。 二分查找 一、什么是二分查找? 二分查找针对的是一个有序的数据集合,每次通过跟区间中间的元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间缩小为0。 二、时间复杂度分析? 1.时间复杂度 时间复杂度是O(logn)。 2.认识O(logn) ①这是一种极其高效的时间复杂度,有时甚至比O(1)的算法还要高效。为什么? ②因为logn是一个非常“恐怖“的数量级,即便n非常大,对应的logn也很小。比如n等于2的32次方,也就是42亿,而logn才32。 ③由此可见,O(logn)有时就是比O(1000),O(10000)快很多。 三、如何实现二分查找? 1.循环实现 代码实现: 注意事项: ①循环退出条件是:start<=end,而不是start 2.递归实现 四、使用条件(应用场景的局限性) 1.二分查找依赖的是顺序表结构,即数组。 2.二分查找针对的是有序数据,因此只能用在插入、删除操作不频繁,一次排序多次查找的场景中。 3.数据量太小不适合二分查找,与直接遍历相比效率提升不明显。但有个例外,就是数据之间的比较操作非常费时,比如数组中存储的都是长度超过300的字符串,那还是尽量减少比较操作使用二分查找。 4.数据量太大也不适合用二分查找,因为数组需要连续的空间,若数据量太大,往往找不到存储如此大规模数据的连续内存空间。 五、思考 1.如何在1000万个整数中快速查找某个整数? ①1000万个整数占用存储空间为40MB,占用空间不大,所以可以全部加载到内存中进行处理; ②用一个1000万个元素的数组存储,然后使用快排进行升序排序,时间复杂度为O(nlogn) ③在有序数组中使用二分查找算法进行查找,时间复杂度为O(logn) 2.如何编程实现“求一个数的平方根”?要求精确到小数点后6位? 求平方根,可以参考0到99之间猜数字的思路,99换成x, 循环到误差允许内即可,注意1这个分界线。 2、二分法求根号5 a:折半: 5/2=2.5 b:平方校验: 2.5 * 2.5=6.25>5,并且得到当前上限2.5 c:再次向下折半:2.5/2=1.25 d:平方校验:1.25 * 1.25=1.5625<5,得到当前下限1.25 e:再次折半:2.5-(2.5-1.25)/2=1.875 f:平方校验:1.875 * 1.875=3.515625<5,得到当前下限1.875 每次得到当前值和5进行比较,并且记下下限和上限,依次迭代,逐渐逼近平方根: 平方根C代码,precision位数,小数点后6位是0.000001 16 | 二分查找(下):如何快速定位IP对应的省份地址? 变体一:查找第一个值等于给定值的元素 写法一: 写法二: 变体二:查找最后一个值等于给定值的元素 变体三:查找第一个大于等于给定值的元素 变体四:查找最后一个小于等于给定值的元素 变体的二分查找算法写起来非常烧脑,容易出错的细节有:终止条件、区间上下界更新方法、返回值选择。 一、四种常见的二分查找变形问题 1.查找第一个值等于给定值的元素 2.查找最后一个值等于给定值的元素 3.查找第一个大于等于给定值的元素 4.查找最后一个小于等于给定值的元素 二、适用性分析 1.凡事能用二分查找解决的,绝大部分更倾向于用散列表或者二叉查找树,即便二分查找在内存上更节省,但是毕竟内存如此紧缺的情况并不多。 2.求“值等于给定值”的二分查找确实不怎么用到,二分查找更适合用在”近似“查找问题上。 三、思考 有三种方法查找循环有序数组 一、 找到分界下标,分成两个有序数组 判断目标值在哪个有序数据范围内,做二分查找 二、 找到最大值的下标 x; 所有元素下标 +x 偏移,超过数组范围值的取模; 利用偏移后的下标做二分查找; 如果找到目标下标,再作 -x 偏移,就是目标值实际下标。 两种情况最高时耗都在查找分界点上,所以时间复杂度是 O(N)。 三、 循环数组存在一个性质:以数组中间点为分区,会将数组分成一个有序数组和一个循环有序数组。 如果首元素小于 mid,说明前半部分是有序的,后半部分是循环有序数组; 如果首元素大于 mid,说明后半部分是有序的,前半部分是循环有序的数组; 如果目标元素在有序数组范围中,使用二分查找; 如果目标元素在循环有序数组中,设定数组边界后,使用以上方法继续查找。 时间复杂度为 O(logN)。 17 | 跳表:为什么Redis一定要用跳表来实现有序集合? 对链表稍加改造,就可以支持类似“二分”的查找算法。我们把改造之后的数据结构叫作跳表。 如何理解“跳表”? 对于一个单链表来讲,即便链表中存储的数据是有序的,如果我们要想在其中查找某个数据,也只能从头到尾遍历链表。这样查找效率就会很低,时间复杂度会很高,是 O(n)。 那怎么来提高查找效率呢?如果对链表建立一级“索引”,每两个结点提取一个结点到上一级,我们把抽出来的那一级叫作索引或索引层。 加来一层索引之后,查找一个结点需要遍历的结点个数减少了,也就是说查找效率提高了。 这种链表加多级索引的结构,就是跳表。 第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2,那第 k级索引结点的个数就是n/(2k)。 在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的。 比起单纯的单链表,跳表需要存储多级索引,肯定要消耗更多的存储空间。 这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以,跳表的空间复杂度是 O(n)。也就是说,如果将包含 n 个结点的单链表构造成跳表,我们需要额外再用接近 n 个结点的存储空间。 高效的动态插入和删除 跳表这个动态数据结构,不仅支持查找操作,还支持动态的插入、删除操作,而且插入、删除操作的时间复杂度也是 O(logn)。 如果这个结点在索引中也有出现,我们除了要删除原始链表中的结点,还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点,然后通过指针操作完成删除。所以在查找要删除的结点的时候,一定要获取前驱结点。如果我们用的是双向链表,就不需要考虑这个问题了。 跳表索引动态更新 当我们不停地往跳表中插入数据时,如果我们不更新索引,就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下,跳表还会退化成单链表。 红黑树、AVL 树这样平衡二叉树,它们是通过左右旋的方式保持左右子树的大小平衡,而跳表是通过随机函数来维护前面提到的“平衡性”。 Redis 中的有序集合是通过跳表来实现的,严格点讲,其实还用到了散列表。 Redis 中的有序集合支持的核心操作主要有下面这几个: 插入一个数据; 删除一个数据; 查找一个数据; 按照区间查找数据(比如查找值在 [100, 356] 之间的数据); 迭代输出有序序列。 其中,插入、删除、查找以及迭代输出有序序列这几个操作,红黑树也可以完成,时间复杂度跟跳表是一样的。但是,按照区间来查找数据这个操作,红黑树的效率没有跳表高。 对于按照区间查找数据这个操作,跳表可以做到 O(logn) 的时间复杂度定位区间的起点,然后在原始链表中顺序往后遍历就可以了。这样做非常高效。 跳表使用空间换时间的设计思路,通过构建多级索引来提高查询的效率,实现了基于链表的“二分查找”。跳表是一种动态数据结构,支持快速的插入、删除、查找操作,时间复杂度都是 O(logn)。 当然,Redis 之所以用跳表来实现有序集合,还有其他原因,比如,跳表更容易代码实现。虽然跳表的实现也不简单,但比起红黑树来说还是好懂、好写多了,而简单就意味着可读性好,不容易出错。还有,跳表更加灵活,它可以通过改变索引构建策略,有效平衡执行效率和内存消耗。 跳表也不能完全替代红黑树。因为红黑树比跳表的出现要早一些,很多编程语言中的 Map 类型都是通过红黑树来实现的。我们做业务开发的时候,直接拿来用就可以了,不用费劲自己去实现一个红黑树,但是跳表并没有一个现成的实现,所以在开发中,如果你想使用跳表,必须要自己实现。 跳表的空间复杂度是 O(n)。不过,跳表的实现非常灵活,可以通过改变索引构建策略,有效平衡执行效率和内存消耗。虽然跳表的代码实现并不简单,但是作为一种动态数据结构,比起红黑树来说,实现要简单多了。所以很多时候,我们为了代码的简单、易读,比起红黑树,我们更倾向用跳表。 18 | 散列表(上):Word文档中的单词拼写检查功能是如何实现的? 散列思想 散列表用的是数组支持按照下标随机访问数据的特性,所以散列表其实就是数组的一种扩展,由数组演化而来。可以说,如果没有数组,就没有散列表。 散列冲突 常用的散列冲突解决方法有两类,开放寻址法(open addressing)和链表法(chaining)。 1. 开放寻址法 开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入。一个比较简单的探测方法,线性探测(Linear Probing)。 当往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,我们就从当前位置开始,依次往后查找,看是否有空闲位置,直到找到为止。 在散列表中查找元素的过程有点儿类似插入过程。我们通过散列函数求出要查找元素的键值对应的散列值,然后比较数组中下标为散列值的元素和要查找的元素。如果相等,则说明就是我们要找的元素;否则就顺序往后依次查找。如果遍历到数组中的空闲位置,还没有找到,就说明要查找的元素并没有在散列表中。 散列表跟数组一样,不仅支持插入、查找操作,还支持删除操作。对于使用线性探测法解决冲突的散列表,不能单纯地把要删除的元素设置为空。 在查找的时候,一旦通过线性探测方法,找到一个空闲位置,就可以认定散列表中不存在这个数据。但是,如果这个空闲位置是后来删除的,就会导致原来的查找算法失效。本来存在的数据,会被认定为不存在。 可以将删除的元素,特殊标记为 deleted。当线性探测查找的时候,遇到标记为 deleted 的空间,并不是停下来,而是继续往下探测。 当散列表中插入的数据越来越多时,散列冲突发生的可能性就会越来越大,空闲位置会越来越少,线性探测的时间就会越来越久。极端情况下,我们可能需要探测整个散列表,所以最坏情况下的时间复杂度为 O(n)。同理,在删除和查找时,也有可能会线性探测整张散列表,才能找到要查找或者删除的数据。 对于开放寻址冲突解决方法,除了线性探测方法之外,还有另外两种比较经典的探测方法,二次探测(Quadratic probing)和双重散列(Double hashing)。 二次探测,跟线性探测很像,线性探测每次探测的步长是 1,而二次探测探测的步长就变成了原来的“二次方”,也就是说,它探测的下标序列就是 hash(key)+0,hash(key)+12,hash(key)+22…… 双重散列,意思就是不仅要使用一个散列函数。我们使用一组散列函数,先用第一个散列函数,如果计算得到的存储位置已经被占用,再用第二个散列函数,依次类推,直到找到空闲的存储位置。 为了尽可能保证散列表的操作效率,一般情况下,我们会尽可能保证散列表中有一定比例的空闲槽位。用装载因子(load factor)来表示空位的多少。 装载因子的计算公式是: 散列表的装载因子 = 填入表中的元素个数 / 散列表的长度 装载因子越大,说明空闲位置越少,冲突越多,散列表的性能会下降。 2. 链表法 链表法是一种更加常用的散列冲突解决办法,它要简单很多。在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。 当插入的时候,只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可,所以插入的时间复杂度是 O(1)。 那查找或删除操作的时间复杂度是多少呢?这两个操作的时间复杂度跟链表的长度 k 成正比,也就是 O(k)。对于散列比较均匀的散列函数来说,理论上讲,k=n/m,其中 n 表示散列中数据的个数,m 表示散列表中“槽”的个数。 散列表来源于数组,它借助散列函数对数组这种数据结构进行扩展,利用的是数组支持按照下标随机访问元素的特性。散列表两个核心问题是散列函数设计和散列冲突解决。散列冲突有两种常用的解决方法,开放寻址法和链表法。散列函数设计的好坏决定了散列冲突的概率,也就决定散列表的性能。 思考 1.Word文档中单词拼写检查功能是如何实现的? 字符串占用内存大小为8字节,20万单词占用内存大小不超过20MB,所以用散列表存储20万英文词典单词,然后对每个编辑进文档的单词进行查找,若未找到,则提示拼写错误。 2.假设我们有10万条URL访问日志,如何按照访问次数给URL排序? 字符串占用内存大小为8字节,10万条URL访问日志占用内存不超过10MB,通过散列表统计url访问次数,然后用TreeMap存储散列表的元素值(作为key)和数组下标值(作为value) 遍历 10 万条数据,以 URL 为 key,访问次数为 value,存入散列表,同时记录下访问次数的最大值 K,时间复杂度 O(N)。 如果 K 不是很大,可以使用桶排序,时间复杂度 O(N)。如果 K 非常大(比如大于 10 万),就使用快速排序,复杂度 O(NlogN)。 3.有两个字符串数组,每个数组大约有10万条字符串,如何快速找出两个数组中相同的字符串? 分别将2个数组的字符串通过散列函数映射到散列表,散列表中的元素值为次数。注意,先存储的数组中的相同元素值不进行次数累加。最后,统计散列表中元素值大于等于2的散列值对应的字符串就是两个数组中相同的字符串。 以第一个字符串数组构建散列表,key 为字符串,value 为出现次数。再遍历第二个字符串数组,以字符串为 key 在散列表中查找,如果 value 大于零,说明存在相同字符串。时间复杂度 O(N)。 19 | 散列表(中):如何打造一个工业级水平的散列表? 如何设计散列函数? 首先,散列函数的设计不能太复杂。其次,散列函数生成的值要尽可能随机并且均匀分布,这样才能避免或者最小化散列冲突,而且即便出现冲突,散列到每个槽里的数据也会比较平均。 装载因子过大了怎么办? 当装载因子过大时,可以进行动态扩容,重新申请一个更大的散列表,将数据搬移到新散列表中。 插入一个数据,最好情况下,不需要扩容,最好时间复杂度是 O(1)。最坏情况下,散列表装载因子过高,启动扩容,我们需要重新申请内存空间,重新计算哈希位置,并且搬移数据,所以时间复杂度是 O(n)。用摊还分析法,均摊情况下,时间复杂度接近最好情况,就是 O(1)。 实际上,对于动态散列表,随着数据的删除,散列表中的数据会越来越少,空闲空间会越来越多。如果对空间消耗非常敏感,可以在装载因子小于某个值之后,启动动态缩容。 当散列表的装载因子超过某个阈值时,就需要进行扩容。装载因子阈值需要选择得当。如果太大,会导致冲突过多;如果太小,会导致内存浪费严重。 装载因子阈值的设置要权衡时间、空间复杂度。如果内存空间不紧张,对执行效率要求很高,可以降低负载因子的阈值;相反,如果内存空间紧张,对执行效率要求又不高,可以增加负载因子的值,甚至可以大于 1。 如何避免低效地扩容? 为了解决一次性扩容耗时过多的情况,可以将扩容操作穿插在插入操作的过程中,分批完成。当装载因子触达阈值之后,只申请新空间,但并不将老的数据搬移到新散列表中。 当有新数据要插入时,将新数据插入新散列表中,并且从老的散列表中拿出一个数据放入到新散列表。每次插入一个数据到散列表,都重复上面的过程。经过多次插入操作之后,老的散列表中的数据就一点一点全部搬移到新散列表中了。这样没有了集中的一次性数据搬移,插入操作就都变得很快了。 对于查询操作,为了兼容了新、老散列表中的数据,先从新散列表中查找,如果没有找到,再去老的散列表中查找。 通过这样均摊的方法,将一次性扩容的代价,均摊到多次插入操作中,就避免了一次性扩容耗时过多的情况。这种实现方式,任何情况下,插入一个数据的时间复杂度都是 O(1)。 如何选择冲突解决方法? Java 中 LinkedHashMap 就采用了链表法解决冲突,ThreadLocalMap 是通过线性探测的开放寻址法来解决冲突。 1. 开放寻址法 散列表中的数据都存储在数组中,可以有效地利用 CPU 缓存加快查询速度。而且,这种方法实现的散列表,序列化起来比较简单。链表法包含指针,序列化起来就没那么容易。 用开放寻址法解决冲突的散列表,删除数据的时候比较麻烦,需要特殊标记已经删除掉的数据。而且,在开放寻址法中,所有的数据都存储在一个数组中,比起链表法来说,冲突的代价更高。所以,使用开放寻址法解决冲突的散列表,装载因子的上限不能太大。这也导致这种方法比链表法更浪费内存空间。 当数据量比较小、装载因子小的时候,适合采用开放寻址法。这也是 Java 中的ThreadLocalMap使用开放寻址法解决散列冲突的原因。 2. 链表法 首先,链表法对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建,并不需要像开放寻址法那样事先申请好。这一点也是链表优于数组的地方。 链表法比起开放寻址法,对大装载因子的容忍度更高。开放寻址法只能适用装载因子小于 1 的情况。接近 1 时,就可能会有大量的散列冲突,导致大量的探测、再散列等,性能会下降很多。但是对于链表法来说,只要散列函数的值随机均匀,即便装载因子变成 10,也就是链表的长度变长了而已,虽然查找效率有所下降,但是比起顺序查找还是快很多。 链表因为要存储指针,所以对于比较小的对象的存储,是比较消耗内存的,还有可能会让内存的消耗翻倍。而且,因为链表中的结点是零散分布在内存中的,不是连续的,所以对 CPU 缓存是不友好的,这方面对于执行效率也有一定的影响。 如果存储的是大对象,也就是说要存储的对象的大小远远大于一个指针的大小(4 个字节或者 8 个字节),那链表中指针的内存消耗在大对象面前就可以忽略了。 对链表法稍加改造,可以实现一个更加高效的散列表。将链表法中的链表改造为其他高效的动态数据结构,比如跳表、红黑树。这样,即便出现散列冲突,极端情况下,所有的数据都散列到同一个桶内,最终退化成的散列表的查找时间也只是 O(logn)。这样也就有效避免了散列碰撞攻击。 基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表,而且,比起开放寻址法,它更加灵活,支持更多的优化策略,比如用红黑树代替链表。 工业级散列表举例分析 1. 初始大小 HashMap 默认的初始大小是 16,如果事先知道大概的数据量有多大,可以通过修改默认初始大小,减少动态扩容的次数,这样会大大提高 HashMap 的性能。 2. 装载因子和动态扩容 最大装载因子默认是 0.75,当 HashMap 中元素个数超过 0.75*capacity(capacity 表示散列表的容量)的时候,就会启动扩容,每次扩容都会扩容为原来的两倍大小。 3. 散列冲突解决方法 HashMap 底层采用链表法来解决冲突。即使负载因子和散列函数设计得再合理,也免不了会出现拉链过长的情况,一旦出现拉链过长,则会严重影响 HashMap 的性能。 于是,在 JDK1.8 版本中,为了对 HashMap 做进一步优化,引入了红黑树。而当链表长度太长(默认超过 8)时,链表就转换为红黑树。利用红黑树快速增删改查的特点,提高 HashMap 的性能。当红黑树结点个数少于 8 个的时候,又会将红黑树转化为链表。因为在数据量较小的情况下,红黑树要维护平衡,比起链表来,性能上的优势并不明显。 4. 散列函数 散列函数的设计并不复杂,追求的是简单高效、分布均匀。 何为一个工业级的散列表?工业级的散列表应该具有哪些特性? 结合已经学习过的散列知识,应该有这样几点要求: 支持快速的查询、插入、删除操作; 内存占用合理,不能浪费过多的内存空间; 性能稳定,极端情况下,散列表的性能也不会退化到无法接受的情况。 如何实现这样一个散列表呢? 根据前面讲到的知识,我会从这三个方面来考虑设计思路: 设计一个合适的散列函数; 定义装载因子阈值,并且设计动态扩容策略; 选择合适的散列冲突解决方法。 关于散列函数的设计,尽可能让散列后的值随机且均匀分布,这样会尽可能地减少散列冲突,即便冲突之后,分配到每个槽内的数据也比较均匀。除此之外,散列函数的设计也不能太复杂,太复杂就会太耗时间,也会影响散列表的性能。 关于散列冲突解决方法的选择,大部分情况下,链表法更加普适。而且,还可以通过将链表法中的链表改造成其他动态查找数据结构,比如红黑树,来避免散列表时间复杂度退化成 O(n),抵御散列碰撞攻击。但是,对于小规模数据、装载因子不高的散列表,比较适合用开放寻址法。 对于动态散列表来说,不管如何设计散列函数,选择什么样的散列冲突解决方法。随着数据的不断增加,散列表总会出现装载因子过高的情况。这个时候,就需要启动动态扩容。 20 | 散列表(下):为什么散列表和链表经常会一起使用? LRU 缓存淘汰算法 如何通过链表实现 LRU 缓存淘汰算法。 维护一个按照访问时间从大到小有序排列的链表结构。因为缓存大小有限,当缓存空间不够,需要淘汰一个数据的时候,我们就直接将链表头部的结点删除。 当要缓存某个数据的时候,先在链表中查找这个数据。如果没有找到,则直接将数据放到链表的尾部;如果找到了,就把它移动到链表的尾部。因为查找数据需要遍历链表,所以单纯用链表实现的 LRU 缓存淘汰算法的时间复杂很高,是 O(n)。 一个缓存(cache)系统主要包含下面这几个操作: 往缓存中添加、删除、查找一个数据; 这三个操作都要涉及“查找”操作,如果单纯地采用链表的话,时间复杂度是 O(n)。如果将散列表和链表两种数据结构组合使用,可以将时间复杂度都降低到 O(1)。具体的结构就是下面这个样子: 使用双向链表存储数据,链表中的每个结点处理存储数据(data)、前驱指针(prev)、后继指针(next)之外,还新增了一个特殊的字段 hnext。这个 hnext 有什么作用呢? 因为我们的散列表是通过链表法解决散列冲突的,所以每个结点会在两条链中。一个链是双向链表,另一个链是散列表中的拉链。前驱和后继指针是为了将结点串在双向链表中,hnext 指针是为了将结点串在散列表的拉链中。 如何查找一个数据。散列表中查找数据的时间复杂度接近 O(1),所以通过散列表,可以很快地在缓存中找到一个数据。当找到数据之后,我们还需要将它移动到双向链表的尾部。 如何删除一个数据。找到数据所在的结点,然后将结点删除。借助散列表,可以在 O(1) 时间复杂度里找到要删除的结点。因为是双向链表,可以通过前驱指针 O(1) 时间复杂度获取前驱结点,所以删除结点只需要 O(1) 的时间复杂度。 如何添加一个数据。添加数据到缓存稍微有点麻烦,先看这个数据是否已经在缓存中。如果已经在其中,需要将其移动到双向链表的尾部;如果不在其中,还要看缓存有没有满。如果满了,则将双向链表头部的结点删除,然后再将数据放到链表的尾部;如果没有满,就直接将数据放到链表的尾部。 Redis 有序集合 在有序集合中,每个成员对象有两个重要的属性,key(键值)和score(分值)。我们不仅会通过 score 来查找数据,还会通过 key 来查找数据。 细化一下 Redis 有序集合的操作,那就是下面这样: 添加一个成员对象; 按照键值来删除一个成员对象; 按照键值来查找一个成员对象; 按照分值区间查找数据,比如查找积分在 [100, 356] 之间的成员对象; 按照分值从小到大排序成员变量; Java LinkedHashMap LinkedHashMap 是通过双向链表和散列表这两种数据结构组合实现的。实际上,它不仅支持按照插入顺序遍历数据,还支持按照访问顺序来遍历数据。LinkedHashMap 中的“Linked”实际上是指的是双向链表,并非指用链表法解决散列冲突。 21 | 哈希算法(上):如何防止数据库中的用户信息被脱库? 什么是哈希算法? 将任意长度的二进制值串映射为固定长度的二进制值串,这个映射的规则就是哈希算法,而通过原始数据映射之后得到的二进制值串就是哈希值。设计一个优秀的哈希算法需要满足的几点要求: 从哈希值不能反向推导出原始数据(所以哈希算法也叫单向哈希算法); 对输入数据非常敏感,哪怕原始数据只修改了一个 Bit,最后得到的哈希值也大不相同; 散列冲突的概率要很小,对于不同的原始数据,哈希值相同的概率非常小; 哈希算法的执行效率要尽量高效,针对较长的文本,也能快速地计算出哈希值。 应用一:安全加密 最常用于加密的哈希算法是MD5(MD5 消息摘要算法)和SHA(安全散列算法)。 除了这两个之外,还有很多其他加密算法,比如DES(数据加密标准)、AES(高级加密标准)。 哈希算法四点要求,对用于加密的哈希算法来说,有两点格外重要。第一点是很难根据哈希值反向推导出原始数据,第二点是散列冲突的概率要很小。 第一点,加密的目的就是防止原始数据泄露,所以很难通过哈希值反向推导原始数据,这是一个最基本的要求。第二点,不管是什么哈希算法,只能尽量减少碰撞冲突的概率,理论上是没办法做到完全不冲突的。 为什么哈希算法无法做到零冲突? 哈希算法产生的哈希值的长度是固定且有限的。比如前面举的 MD5 的例子,哈希值是固定的 128 位二进制串,能表示的数据是有限的,最多能表示 2128 个数据,而我们要哈希的数据是无穷的。基于鸽巢原理,如果我们对 2128+1 个数据求哈希值,就必然会存在哈希值相同的情况。一般情况下,哈希值越长的哈希算法,散列冲突的概率越低。 即便哈希算法存在散列冲突的情况,但是因为哈希值的范围很大,冲突的概率极低,所以相对来说还是很难破解的。 应用二:唯一标识 如果要在海量的图库中,搜索一张图是否存在,我们不能单纯地用图片的元信息(比如图片名称)来比对,因为有可能存在名称相同但图片内容不同,或者名称不同图片内容相同的情况。那该如何搜索呢? 可以给每一个图片取一个唯一标识,或者说信息摘要。通过这个唯一标识来判定图片是否在图库中,这样就可以减少很多工作量。 如果还想继续提高效率,可以把每个图片的唯一标识,和相应的图片文件在图库中的路径信息,都存储在散列表中。当要查看某个图片是不是在图库中的时候,先通过哈希算法对这个图片取唯一标识,然后在散列表中查找是否存在这个唯一标识。 如果不存在,那就说明这个图片不在图库中;如果存在,再通过散列表中存储的文件路径,获取到这个已经存在的图片,跟现在要插入的图片做全量的比对,看是否完全一样。如果一样,就说明已经存在;如果不一样,说明两张图片尽管唯一标识相同,但是并不是相同的图片。 应用三:数据校验 BT 下载的原理是基于 P2P 协议的。从多个机器上并行下载一个 2GB 的电影,这个电影文件可能会被分割成很多文件块。等所有的文件块都下载完成之后,再组装成一个完整的电影文件就行了。 可以通过哈希算法,对 100 个文件块分别取哈希值,并且保存在种子文件中。只要文件块的内容有一丁点儿的改变,最后计算出的哈希值就会完全不同。所以,当文件块下载完成之后,可以通过相同的哈希算法,对下载好的文件块逐一求哈希值,然后跟种子文件中保存的哈希值比对。如果不同,说明这个文件块不完整或者被篡改了,需要再重新从其他宿主机器上下载这个文件块。 应用四:散列函数 实际上,散列函数也是哈希算法的一种应用。 散列函数是设计一个散列表的关键。它直接决定了散列冲突的概率和散列表的性能。相对哈希算法的其他应用,散列函数对于散列算法冲突的要求要低很多。即便出现个别散列冲突,只要不是过于严重,都可以通过开放寻址法或者链表法解决。 不仅如此,散列函数对于散列算法计算得到的值,是否能反向解密也并不关心。散列函数中用到的散列算法,更加关注散列后的值是否能平均分布,也就是,一组数据是否能均匀地散列在各个槽中。除此之外,散列函数执行的快慢,也会影响散列表的性能,所以,散列函数用的散列算法一般都比较简单,比较追求效率。 字典攻击你听说过吗?如果用户信息被“脱库”,黑客虽然拿到是加密之后的密文,但可以通过“猜”的方式来破解密码,这是因为,有些用户的密码太简单。 那就需要维护一个常用密码的字典表,把字典中的每个密码计算哈希值,然后跟脱库后的密文比对。如果相同,基本上就可以认为,这个加密之后的密码对应的明文就是字典中的这个密码。 针对字典攻击,我们可以引入一个盐(salt),跟用户的密码组合在一起,增加密码的复杂度。拿组合之后的字符串来做哈希算法加密,将它存储到数据库中,进一步增加破解的难度。 哈希算法的四个应用场景。 第一个应用是唯一标识,哈希算法可以对大数据做信息摘要,通过一个较短的二进制编码来表示很大的数据。 第二个应用是用于校验数据的完整性和正确性。 第三个应用是安全加密,任何哈希算法都会出现散列冲突,但是这个冲突概率非常小。越是复杂哈希算法越难破解,但同样计算时间也就越长。所以,选择哈希算法的时候,要权衡安全性和计算时间来决定用哪种哈希算法。 第四个应用是散列函数,它对哈希算法的要求非常特别,更加看重的是散列的平均性和哈希算法的执行效率。 22 | 哈希算法(下):哈希算法在分布式系统中有哪些应用? 应用五:负载均衡 负载均衡算法有很多,比如轮询、随机、加权轮询等。那如何才能实现一个会话粘滞(session sticky)的负载均衡算法呢?也就是说,需要在同一个客户端上,在一次会话中的所有请求都路由到同一个服务器上。 最直接的方法就是,维护一张映射关系表,这张表的内容是客户端 IP 地址或者会话 ID 与服务器编号的映射关系。客户端发出的每次请求,都要先在映射表中查找应该路由到的服务器编号,然后再请求编号对应的服务器。这种方法简单直观,但也有几个弊端: 如果客户端很多,映射表可能会很大,比较浪费内存空间; 客户端下线、上线,服务器扩容、缩容都会导致映射失效,这样维护映射表的成本就会很大; 可以通过哈希算法,对客户端 IP 地址或者会话 ID 计算哈希值,将取得的哈希值与服务器列表的大小进行取模运算,最终得到的值就是应该被路由到的服务器编号。这样,我们就可以把同一个 IP 过来的所有请求,都路由到同一个后端服务器上。 应用六:数据分片 1. 如何统计“搜索关键词”出现的次数? 假如我们有 1T 的日志文件,这里面记录了用户的搜索关键词,我们想要快速统计出每个关键词被搜索的次数,该怎么做呢? 这个问题有两个难点,第一个是搜索日志很大,没办法放到一台机器的内存中。第二个难点是,如果只用一台机器来处理这么巨大的数据,处理时间会很长。 针对这两个难点,可以先对数据进行分片,然后采用多台机器处理的方法,来提高处理速度。具体的思路:为了提高处理的速度,用 n 台机器并行处理。从搜索记录的日志文件中,依次读出每个搜索关键词,通过哈希函数计算哈希值,然后再跟 n 取模,最终得到的值,就是应该被分配到的机器编号。 这样,哈希值相同的搜索关键词就被分配到了同一个机器上。每个机器会分别计算关键词出现的次数,最后合并起来就是最终的结果。 实际上,这里的处理过程也是 MapReduce 的基本设计思想。 2. 如何快速判断图片是否在图库中? 如何快速判断图片是否在图库中?即给每个图片取唯一标识(或者信息摘要),然后构建散列表。 假设现在我们的图库中有 1 亿张图片,在单台机器上构建散列表是行不通的。 同样可以对数据进行分片,然后采用多机处理。准备 n 台机器,让每台机器只维护某一部分图片对应的散列表。每次从图库中读取一个图片,计算唯一标识,然后与机器个数 n 求余取模,得到的值就对应要分配的机器编号,然后将这个图片的唯一标识和图片路径发往对应的机器构建散列表。 当判断一个图片是否在图库中的时候,通过同样的哈希算法,计算这个图片的唯一标识,然后与机器个数 n 求余取模。假设得到的值是 k,那就去编号 k 的机器构建的散列表中查找。 实际上,针对这种海量数据的处理问题,都可以采用多机分布式处理。借助这种分片的思路,可以突破单机内存、CPU 等资源的限制。 应用七:分布式存储 现在互联网面对的都是海量的数据、海量的用户。为了提高数据的读取、写入能力,一般都采用分布式的方式来存储数据,比如分布式缓存。需要将数据分布在多台机器上。 该如何决定将哪个数据放到哪个机器上呢?可以借用数据分片的思想,即通过哈希算法对数据取哈希值,然后对机器个数取模,这个最终值就是应该存储的缓存机器编号。 但是,如果数据增多,原来的 10 个机器已经无法承受了,我们就需要扩容了,比如扩到 11 个机器,这时候麻烦就来了。因为,这里并不是简单地加个机器就可以了。 所有的数据都要重新计算哈希值,然后搬移到正确的机器上。这样就相当于,缓存中的数据一下子就都失效了。所有的数据请求都会穿透缓存,直接去请求数据库。这样就可能发生雪崩效应,压垮数据库。 需要一种方法,使得在新加入一个机器后,不需要做大量的数据搬移。一致性哈希算法就登场了。 假设我们有 k 个机器,数据的哈希值的范围是 [0, MAX]。我们将整个范围划分成 m 个小区间(m 远大于 k),每个机器负责 m/k 个小区间。当有新机器加入的时候,我们就将某几个小区间的数据,从原来的机器中搬移到新的机器中。这样,既不用全部重新哈希、搬移数据,也保持了各个机器上数据数量的均衡。 负载均衡应用中,利用哈希算法替代映射表,可以实现一个会话粘滞的负载均衡策略。在数据分片应用中,通过哈希算法对处理的海量数据进行分片,多机分布式处理,可以突破单机资源的限制。在分布式存储应用中,利用一致性哈希算法,可以解决缓存等分布式系统的扩容、缩容导致数据大量搬移的难题。// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {
return bsearchInternally(a, 0, n - 1, val);
}
private int bsearchInternally(int[] a, int low, int high, int value) {
if (low > high) return -1;
int mid = low + ((high - low) >> 1);
if (a[mid] == value) {
return mid;
} else if (a[mid] < value) {
return bsearchInternally(a, mid+1, high, value);
} else {
return bsearchInternally(a, low, mid-1, value);
}
}public int binarySearch1(int[] a, int val){
int start = 0;
int end = a.length - 1;
while(start <= end){
int mid = start + (end - start) / 2;
if(a[mid] > val) end = mid - 1;
else if(a[mid] < val) start = mid + 1;
else return mid;
}
return -1;
}public int binarySearch(int[] a, int val){
return bSear(a, val, 0, a.length-1);
}
private int bSear(int[] a, int val, int start, int end) {
if(start > end) return -1;
int mid = start + (end - start) / 2;
if(a[mid] == val) return mid;
else if(a[mid] > val) end = mid - 1;
else start = mid + 1;
return bSear(a, val, start, end);
}public static double sqrt(double x, double precision) {
if (x < 0) {
return Double.NaN;
}
double low = 0;
double up = x;
if (x < 1 && x > 0) {
/** 小于1的时候*/
low = x;
up = 1;
}
double mid = low + (up - low)/2;
while(up - low > precision) {
if (mid * mid > x ) {//TODO mid可能会溢出
up = mid;
} else if (mid * mid < x) {
low = mid;
} else {
return mid;
}
mid = low + (up - low)/2;
}
return mid;
}double squareRoot(double a , double precision){
double low,high,mid,tmp;
if (a>1){
low = 1;
high = a;
}else{
low = a;
high = 1;
}
while (low<=high) {
mid = (low+high)/2.000;
tmp = mid*mid;
if (tmp-a <= precision && tmp-a >= precision*-1){
return mid;
}else if (tmp>a){
high = mid;
}else{
low = mid;
}
}
return -1.000;
}
int main(int argc, const char * argv[]) {
double num = squareRoot(2, 0.000001);
printf("%f",num);
return 0;
}public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
high = mid - 1;
} else {
low = mid + 1;
}
}
if (low < n && a[low]==value) return low;
else return -1;
}public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == 0) || (a[mid - 1] != value)) return mid;
else high = mid - 1;
}
}
return -1;
}public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
else low = mid + 1;
}
}
return -1;
}public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
if ((mid == 0) || (a[mid - 1] < value)) return mid;
else high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}
public int bsearch7(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else {
if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
else low = mid + 1;
}
}
return -1;
}
int hash(Object key) {
int h = key.hashCode();
return (h ^ (h >>> 16)) & (capitity -1); //capicity 表示散列表的大小
}