《动手学深度学习 Pytorch版》 9.2 长短期记忆网络(LSTM)
解决隐变量模型长期信息保存和短期输入缺失问题的最早方法之一是长短期存储器(long short-term memory,LSTM)。它与门控循环单元有许多一样的属性。长短期记忆网络的设计比门控循环单元稍微复杂一些,却比门控循环单元早诞生了近 20 年。
9.2.1 门控记忆元
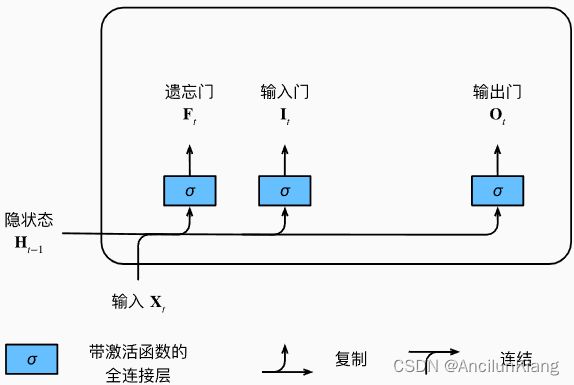
为了记录附加的信息,长短期记忆网络引入了与隐状态具有相同的形状的记忆元(memory cell),或简称为单元(cell)。
为了控制记忆元又需要引入许多门:
-
输出门(output gate):用来从单元中输出条目,决定是不是使用隐藏状态。
-
输入门(input gate):用来决定何时将数据读入单元,决定是不是忽略掉输入数据。
-
遗忘门(forget gate):用来重置单元的内容,将值朝 0 减少。
这种设计的动机与门控循环单元相同, 能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。
9.2.1.1 输入门、遗忘门和输出门
特征:
-
以当前时间步的输入和前一个时间步的隐状态为数据送入长短期记忆网络的门
-
由三个具有 sigmoid 激活函数的全连接层计算输入门、遗忘门和输出门的值
-
值都在的 ( 0 , 1 ) (0,1) (0,1) 范围内
它们的计算方法如下:
I t = σ ( X t W x i + H t − 1 W h i + b i ) F t = σ ( X t W x f + H t − 1 W h f + b f ) O t = σ ( X t W x o + H t − 1 W h o + b o ) \begin{align} \boldsymbol{I}_t&=\sigma(\boldsymbol{X}_t\boldsymbol{W}_{xi}+\boldsymbol{H}_{t-1}\boldsymbol{W}_{hi}+b_i)\\ \boldsymbol{F}_t&=\sigma(\boldsymbol{X}_t\boldsymbol{W}_{xf}+\boldsymbol{H}_{t-1}\boldsymbol{W}_{hf}+b_f)\\ \boldsymbol{O}_t&=\sigma(\boldsymbol{X}_t\boldsymbol{W}_{xo}+\boldsymbol{H}_{t-1}\boldsymbol{W}_{ho}+b_o) \end{align} ItFtOt=σ(XtWxi+Ht−1Whi+bi)=σ(XtWxf+Ht−1Whf+bf)=σ(XtWxo+Ht−1Who+bo)
参数列表:
-
X t ∈ R n × d \boldsymbol{X}_t\in\R^{n\times d} Xt∈Rn×d 表示小批量输入
-
n n n 表示批量大小
-
d d d 表示输入个数
-
-
H t − 1 ∈ R n × h \boldsymbol{H}_{t-1}\in\R^{n\times h} Ht−1∈Rn×h 表示上一个时间步的隐状态
- h h h 表示隐藏单元个数
-
I t ∈ R n × h \boldsymbol{I}_t\in\R^{n\times h} It∈Rn×h 表示输入门
-
F t ∈ R n × h \boldsymbol{F}_t\in\R^{n\times h} Ft∈Rn×h 表示遗忘门
-
O t ∈ R n × h \boldsymbol{O}_t\in\R^{n\times h} Ot∈Rn×h 表示输出门
-
W x i , W x f , W x o ∈ R d × h \boldsymbol{W}_{xi},\boldsymbol{W}_{xf},\boldsymbol{W}_{xo}\in\R^{d\times h} Wxi,Wxf,Wxo∈Rd×h 和 W h i , W h f , W h o ∈ R h × h \boldsymbol{W}_{hi},\boldsymbol{W}_{hf},\boldsymbol{W}_{ho}\in\R^{h\times h} Whi,Whf,Who∈Rh×h 表示权重参数
-
b i , b f , b o ∈ R 1 × h b_i,b_f,b_o\in\R^{1\times h} bi,bf,bo∈R1×h 表示偏重参数
9.2.1.2 候选记忆单元
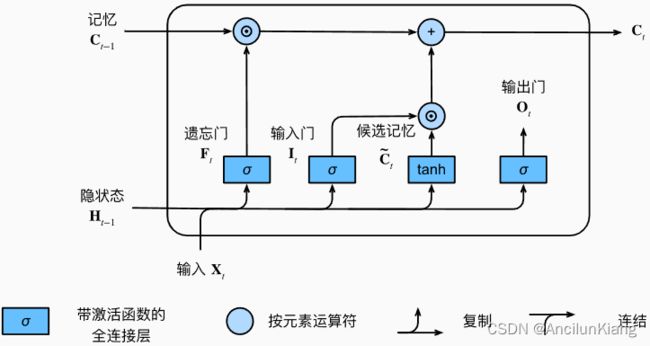
候选记忆元(candidate memory cell) C t ~ ∈ R n × h \tilde{\boldsymbol{C}_t}\in\R^{n\times h} Ct~∈Rn×h 的计算与上面描述的三个门的计算类似,但是使用 tanh 函数作为激活函数,函数的值范围为 ( 0 , 1 ) (0,1) (0,1)。
它的计算方式如下:
C t ~ = t a n h ( X t W x c + H t − 1 W h c + b c ) \tilde{\boldsymbol{C}_t}=tanh(\boldsymbol{X}_t\boldsymbol{W}_{xc}+\boldsymbol{H}_{t-1}\boldsymbol{W}_{hc}+\boldsymbol{b}_c) Ct~=tanh(XtWxc+Ht−1Whc+bc)
参数列表:
-
W x c ∈ R d × h \boldsymbol{W}_{xc}\in\R^{d\times h} Wxc∈Rd×h 和 W h c ∈ R h × h \boldsymbol{W}_{hc}\in\R^{h\times h} Whc∈Rh×h 表示权重参数
-
b c ∈ R 1 × h \boldsymbol{b}_c\in\R^{1\times h} bc∈R1×h 表示偏置参数
9.2.1.3 记忆元
-
输入门 I t I_t It 控制采用多少来自 C t ~ \tilde{\boldsymbol{C}_t} Ct~ 的新数据
-
遗忘门 F t F_t Ft 控制保留多少过去的记忆元 C t − 1 ∈ R n × h \boldsymbol{C}_{t-1}\in\R^{n\times h} Ct−1∈Rn×h 的内容。
计算方法:
C t = F t ⊙ C t − 1 + I t ⊙ C t ~ \boldsymbol{C}_t=\boldsymbol{F}_t\odot\boldsymbol{C}_{t-1}+\boldsymbol{I}_t\odot\tilde{\boldsymbol{C}_t} Ct=Ft⊙Ct−1+It⊙Ct~
如果遗忘门始终为 1 且输入门始终为 0,则过去的记忆元 C t − 1 \boldsymbol{C}_{t-1} Ct−1 将随时间被保存并传递到当前时间步。
引入这种设计是为了:
9.2.1.4 隐状态
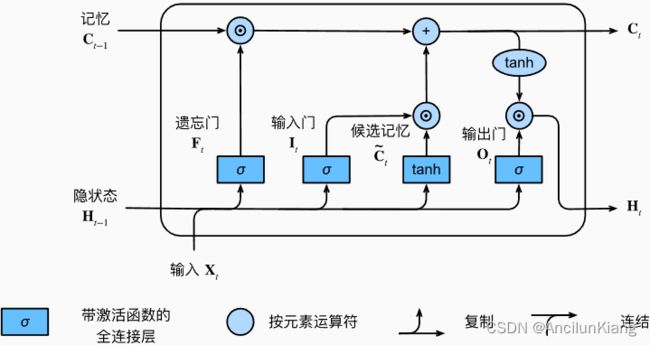
计算隐状态 H t ∈ R n × h \boldsymbol{H}_t\in\R^{n\times h} Ht∈Rn×h 是输出门发挥作用的地方。实际上它仅仅是记忆元的 tanh 的门控版本。 这就确保了 H t \boldsymbol{H}_t Ht 的值始终在区间 ( − 1 , 1 ) (-1,1) (−1,1)内:
H t = O t ⊙ t a n h ( C t ) \boldsymbol{H}_t=\boldsymbol{O}_t\odot tanh(\boldsymbol{C}_t) Ht=Ot⊙tanh(Ct)
只要输出门接近 1,我们就能够有效地将所有记忆信息传递给预测部分,而对于输出门接近 0,我们只保留记忆元内的所有信息,而不需要更新隐状态。
9.2.2 从零开始实现
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
9.2.2.1 初始化模型参数
def get_lstm_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device)*0.01
def three():
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xi, W_hi, b_i = three() # 输入门参数
W_xf, W_hf, b_f = three() # 遗忘门参数
W_xo, W_ho, b_o = three() # 输出门参数
W_xc, W_hc, b_c = three() # 候选记忆元参数
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
b_c, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
9.2.2.2 定义模型
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), # 隐状态需要返回一个额外的单元的值为0形状为(批量大小,隐藏单元数)记忆元
torch.zeros((batch_size, num_hiddens), device=device))
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i) # 输入门运算
F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f) # 遗忘门运算
O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o) # 输出门运算
C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c) # 候选记忆元运算
C = F * C + I * C_tilda # 记忆元计算
H = O * torch.tanh(C) # 隐状态计算
Y = (H @ W_hq) + b_q # 输出计算
outputs.append(Y)
return torch.cat(outputs, dim=0), (H, C)
9.2.2.3 训练与预测
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,
init_lstm_state, lstm)
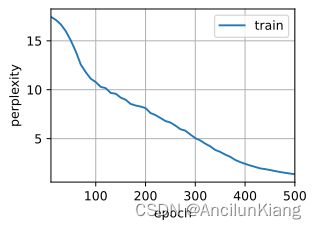
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
perplexity 1.1, 28093.3 tokens/sec on cuda:0
time traveller well pnatter ats sho in the geet on the battle of
traveller oft chat in all dore think of mowh of stace assio
9.2.3 简洁实现
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
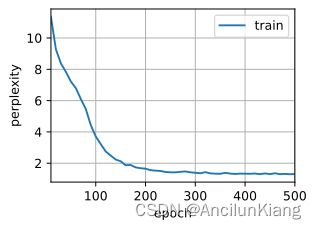
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
perplexity 1.0, 171500.8 tokens/sec on cuda:0
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby
练习
(1)调整和分析超参数对运行时间、困惑度和输出顺序的影响。
跟上一节类似,五个参数轮着换。
def test(Hyperparameters): # [batch_size, num_steps, num_hiddens, lr, num_epochs]
train_iter_now, vocab_now = d2l.load_data_time_machine(Hyperparameters[0], Hyperparameters[1])
lstm_layer_now = nn.LSTM(len(vocab_now), Hyperparameters[2])
model_now = d2l.RNNModel(lstm_layer_now, len(vocab_now))
model_now = model_now.to(d2l.try_gpu())
d2l.train_ch8(model_now, train_iter_now, vocab_now, Hyperparameters[3], Hyperparameters[4], d2l.try_gpu())
Hyperparameters_lists = [
[64, 35, 256, 1, 500], # 加批量大小
[32, 64, 256, 1, 500], # 加时间步
[32, 35, 512, 1, 500], # 加隐藏单元数
[32, 35, 256, 0.5, 500], # 减半学习率
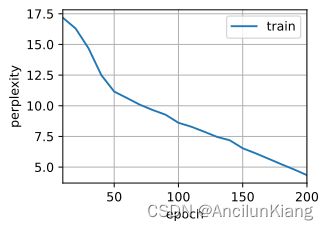
[32, 35, 256, 1, 200] # 减轮数
]
for Hyperparameters in Hyperparameters_lists:
test(Hyperparameters)
perplexity 4.3, 164389.7 tokens/sec on cuda:0
time traveller the the that the grome that he a thee tho ghith o
traveller the that that that this that the go that have the
(2)如何更改模型以生成适当的单词,而不是字符序列?
浅浅的改了一下预测函数和训练函数。
def predict_ch8_word(prefix, num_preds, net, vocab, device): # 词预测
"""在prefix后面生成新字符"""
state = net.begin_state(batch_size=1, device=device)
outputs = [vocab[prefix[0]]] # 调用 vocab 类的 __getitem__ 方法
get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1)) # 把预测结果(结果的最后一个)作为下一个的输入
for y in prefix[1:]: # 预热期 把前缀先载进模型
_, state = net(get_input(), state)
outputs.append(vocab[y])
for _ in range(num_preds): # 预测 num_preds 步
y, state = net(get_input(), state)
outputs.append(int(y.argmax(dim=1).reshape(1))) # 优雅
return ''.join([vocab.idx_to_token[i] + ' ' for i in outputs]) # 加个空格分隔各词
def train_ch8_word(net, train_iter, vocab, lr, num_epochs, device, # 词训练
use_random_iter=False):
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
legend=['train'], xlim=[10, num_epochs])
# 初始化
if isinstance(net, nn.Module):
updater = torch.optim.SGD(net.parameters(), lr)
else:
updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
predict = lambda prefix: predict_ch8_word(prefix, 50, net, vocab, device)
# 训练和预测
for epoch in range(num_epochs):
ppl, speed = d2l.train_epoch_ch8(
net, train_iter, loss, updater, device, use_random_iter)
if (epoch + 1) % 10 == 0:
print(predict(['time', 'traveller'])) # 使用 word 而非 char
animator.add(epoch + 1, [ppl])
print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
print(predict(['time', 'traveller']))
print(predict(['traveller']))
class SeqDataLoader_word: # 词加载器
def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):
if use_random_iter:
self.data_iter_fn = d2l.seq_data_iter_random
else:
self.data_iter_fn = d2l.seq_data_iter_sequential
lines = d2l.read_time_machine()
tokens = d2l.tokenize(lines, token='word') # 使用 word 而非 char
self.vocab_word = d2l.Vocab(tokens) # 构建 word 词表
self.corpus_word = [self.vocab_word[token] for line in tokens for token in line]
if max_tokens > 0:
self.corpus_word = self.corpus_word[:max_tokens]
self.batch_size, self.num_steps = batch_size, num_steps
def __iter__(self):
return self.data_iter_fn(self.corpus_word, self.batch_size, self.num_steps)
train_iter_word = SeqDataLoader_word(
64, 35, False, 10000)
vocab_word = train_iter_word.vocab_word
lstm_layer_word = nn.LSTM(len(vocab_word), 256)
model_word = d2l.RNNModel(lstm_layer_word, len(vocab_word))
model_word = model_word.to(d2l.try_gpu())
train_ch8_word(model_word, train_iter_word, vocab_word, 1.5, 1000, d2l.try_gpu())
困惑度 1.7, 40165.1 词元/秒 cuda:0
time traveller s his hand at last to me that with his own to the psychologist with his grew which i had said filby time travelling yes said the time traveller with his mouth full nodding his head i d give a shilling a line for a verbatim note said the editor
traveller and i was so the sun in my marble smote to the world for for the long pressed he was the little of the sun and presently for a certain heap of cushions and robes i saw on the sun in my confident anticipations it seemed a large figure of
(3)在给定隐藏层维度的情况下,比较门控循环单元、长短期记忆网络和常规循环神经网络的计算成本。要特别注意训练和推断成本。
咋好像每个都差不多。
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
num_inputs = len(vocab)
device = d2l.try_gpu()
num_hiddens = 256
num_epochs, lr = 500, 1
rnn_layer = nn.RNN(len(vocab), num_hiddens)
model_RNN = d2l.RNNModel(rnn_layer, vocab_size=len(vocab))
model_RNN = model_RNN.to(device)
d2l.train_ch8(model_RNN, train_iter, vocab, lr, num_epochs, device) # 34.3s
perplexity 1.3, 218374.6 tokens/sec on cuda:0
time travelleryou can show black is whith basimat very hu and le
travellerit so drawly us our dimsas absulladt nt havi gerea
gru_layer = nn.GRU(num_inputs, num_hiddens)
model_GRU = d2l.RNNModel(gru_layer, len(vocab))
model_GRU = model_GRU.to(device)
d2l.train_ch8(model_GRU, train_iter, vocab, lr, num_epochs, device) # 35.1s
perplexity 1.0, 199203.7 tokens/sec on cuda:0
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model_LSTM = d2l.RNNModel(lstm_layer, len(vocab))
model_LSTM = model_LSTM.to(device)
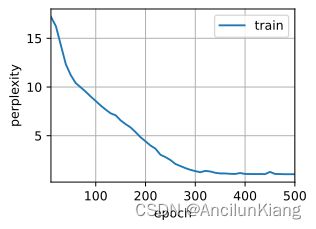
d2l.train_ch8(model_LSTM, train_iter, vocab, lr, num_epochs, device) # 35.4s
perplexity 1.0, 199069.6 tokens/sec on cuda:0
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby
(4)既然候选记忆元通过使用 tanh 函数来确保值范围在 ( − 1 , 1 ) (-1,1) (−1,1) 之间,那么为什么隐状态需要再次使用 tanh 函数来确保输出值范围在 (-1,1) 之间呢?
候选记忆元和隐状态之间还有个记忆元呐,这个: C t = F t ⊙ C t − 1 + I t ⊙ C t ~ \boldsymbol{C}_t=\boldsymbol{F}_t\odot\boldsymbol{C}_{t-1}+\boldsymbol{I}_t\odot\tilde{\boldsymbol{C}_t} Ct=Ft⊙Ct−1+It⊙Ct~
很有可能出范围的。
(5)实现一个能够基于时间序列进行预测而不是基于字符序列进行预测的长短期记忆网络模型。
不会,略。