python实现lagrange插值法
在文章最后可复制代码,已封装直接调用即可。
一、引言
二、历史发展
三、内容总结
3.1 多项式插值问题
3.2 基函数
3.3 拉格朗日插值多项式
3.4 插值余项
四、代码复现部分讲解
这里给出了每步骤的复现与例题验证,读者也可自己进行编写,加深理解。在后文也给出完整代码,可直接拿去使用。
4.1 求解拉格朗日基函数
4.2 基于拉格朗日算法拟合所需要的插值节点
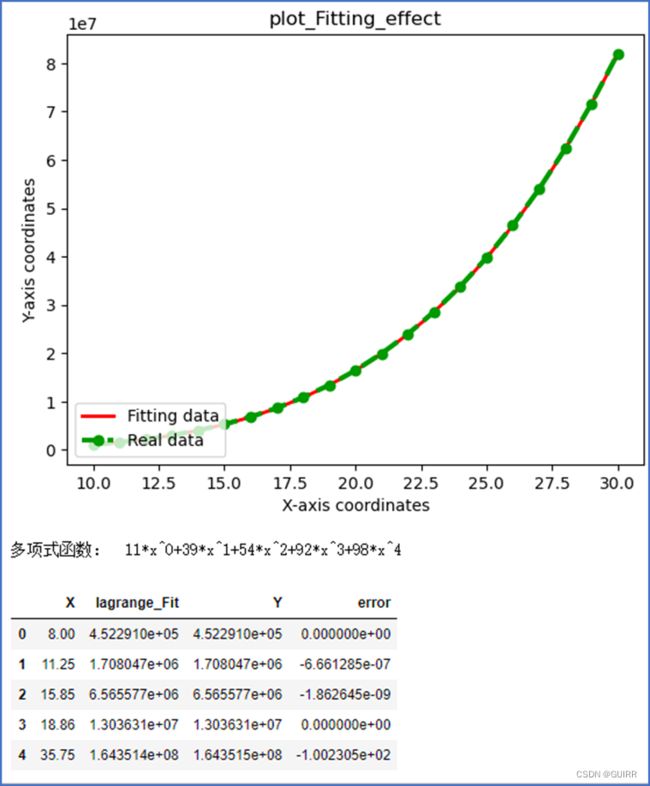
4.3 可视化拟合效果
4.4 更新数值和重新选择算法
五、数据验证
5.1 用过点(-1,-1),(1,0),(3,-6) ,(4,3)的抛物线插值(即三次插值多项式) 求x=0, x=2, x=5的近似值。
5.2 随机生成n次多项式,随机挑选N个点,并求出对应的近似值与误差。
① 随机构造n次多项式,并返回对应函数Y值

② 构造5次多项式,且系数范围为[1-100]

③ 开始拟合并验证结果

六 完整代码
6.1 lagrange算法
# 1.导入相关库
import matplotlib as mpl
import matplotlib.pyplot as plt
from sympy import *
import numpy as np
class Interpolation():
def __init__(self,algorithm="lagrange"):
self.algorithm = algorithm # 选择算法
def Nderivative(self,Y,N): # 递归获取函数Y的N阶导数
if N==0:return Y
Y = diff(Y,symbols("x"))
if N==1:return Y
return self.Nderivative(Y,N-1)
def get_hierarchy(self,n):# 递归获取n的阶层
if n==1:return 1
return n*self.get_hierarchy(n-1)
def Truncation_error_limit(self,Y,Xi): # 误差限
Y_Nderivative = self.Nderivative(Y,self.n+1) # 函数Y的n+1阶求导
# max_Y_Nd = 获取函数n+1阶导数的最值
hierarchy = self.get_hierarchy(self.n+1) # 获取n+1的阶层
W = 1
for Xj in self.X:W*=(Xi-Xj)
xishu = W/hierarchy
return str(xishu)+"*"+str(Y_Nderivative)
# --------------------------------- lagrange 插值法 ------------------------------
def lagrange_ln_fun(self,k,predict_x): # 基函数
molecule,denominator = 1,1 # 分子分母
for i in range(self.n+1):
if i!=k:
molecule = molecule*(predict_x-self.X[i])
denominator = denominator*(self.X[k]-self.X[i])
return molecule/denominator
def lagrange_operation(self):
for predict_x in self.predict_X: # 计算每个插值的单个数据
Ln_fun = 0 # 拉格朗日插值多项式,返回单个数据的插值
for k in range(self.n+1):
Ln_fun += self.Y[k]*self.lagrange_ln_fun(k,predict_x)
self.predict_Y.append(Ln_fun)
return self.predict_Y
def lagrange_prepare_data(self,X,Y,predict_X):
# 更新X,Y,predict_X数组
if len(X):
self.X , self.n = X , len(X)-1 # n次项式
if len(Y):self.Y = Y
if len(predict_X):
self.predict_X , self.predict_Y = predict_X , []
# 此时要插值的值也是要更新的
return self.lagrange_operation()
# ------------------------------可视化:仅限于单维度---------------------------------
def plot_Fitting_effect(self):
real_X,real_Y = self.X,self.Y
xlim = np.linspace(min(self.X), max(self.X), num=int(3*len(self.X)), endpoint=True)
plot_fit_Y = self.lagrange_prepare_data(self.X,self.Y,xlim)
self.X = real_X # 将真正训练数据返回原位
self.Y = real_Y # 将真正训练数据返回原位
# Make the plot
plt.plot(xlim, plot_fit_Y, linewidth=2,label=r"Fitting data",color="red")
plt.plot(real_X,real_Y,"go--", linewidth=3,label=r"Real data")
plt.xlabel(r"X-axis coordinates")
plt.ylabel(r"Y-axis coordinates")
plt.title(r"plot_Fitting_effect")
plt.legend(loc='lower left')
plt.show()
# ---------------------------------主函数 ---------------------------------------------
def predict(self,X=[],Y=[],predict_X=[],algorithm="",plot=False):
self.plot=plot
if algorithm:self.algorithm = algorithm # 更新插值算法
# ----------------------使用拉格朗日插值算法---------------------
if self.algorithm == "lagrange":
value = self.lagrange_prepare_data(X,Y,predict_X)
if self.plot:self.plot_Fitting_effect()
return value
# 传入初始数据: X,Y都是1维数组
# predict_X为预测数组,即插值数据数组
# algorithm为选择算法
'''pass,后续更新其余算法'''
6.2 案例代码
import random
'''随机生成n次多项式函数'''
def get_polynomial_function(Number_range,N):
coefficient ,string= [],""
for i in range(N):
coefficient.append(random.randint(1,Number_range))
string += str(coefficient[-1])+"*x^{}+".format(i)
return coefficient,string[:-1]
'''传入多项式系数与X值,返回函数Y值'''
def calculation(coefficient,x):
return sum([coef*x**n for n,coef in enumerate(coefficient)])
coefficient,string = get_polynomial_function(100,5) # 构造5次多项式,且系数为【1-100】
X = [number for number in range(10,31)] # 构造节点X=[10,30],用于训练朗格朗日插值法
coefficients = [coefficient for i in range(len(X))] # 系数列表
Y = list(map(calculation,coefficients,X)) # 获取变量X对应多项式Y的真实值
model = Interpolation() # 读取封装好类
predict_X = [8,11.25,15.85,18.86,35.75] # 训练后预测f(predict_X)
predict_Y = model.predict(X,Y,predict_X,plot=True) # 调用朗格朗日插值法
predictX_Y = list(map(calculation,coefficients,predict_X )) # 获取变量待预测值对应多项式Y的真实值
print("多项式函数: ",string)
data = pd.DataFrame()
data["X"] = predict_X
data[ 'lagrange_Fit'] = predict_Y
data['Y'] = predictX_Y
data["error"] = [predict_Y[i]-predictX_Y[i] for i in range(len(predict_X))]
data
七 总结
算法是一个插值算法的实现,目前只包含了拉格朗日插值算法。代码总结为以下几个部分:
- 导入相关库:导入matplotlib和sympy库,用于绘图和符号计算。
- Interpolation类的定义:包含了初始化函数和各种方法。
- Nderivative方法:递归获取函数Y的N阶导数。
- get_hierarchy方法:递归获取n的阶层。
- Truncation_error_limit方法:计算误差限。
- lagrange_ln_fun方法:计算拉格朗日插值基函数。
- lagrange_operation方法:使用拉格朗日插值法进行插值操作。
- lagrange_prepare_data方法:准备插值所需的数据。
- predict方法:根据给定的算法进行插值预测。
- plot_Fitting_effect方法:可视化拟合效果。
- 主函数部分:根据选择的算法调用相应的方法进行插值预测。
本代码实现了插值算法的一个类Interpolation,目前包括拉格朗日插值法的实现。通过该类可以进行插值预测,并可选择是否进行可视化展示。具体功能包括:
- 递归获取函数的高阶导数。
- 计算阶层和误差限。
- 使用拉格朗日插值法进行插值操作。
- 准备插值所需的数据。
- 进行插值预测,并可选择是否进行可视化展示。
该代码可以用于对一维数据进行插值分析,例如根据给定的数据点,通过拉格朗日插值法预测其他数据点的值。你可以根据需要扩展其他插值算法的实现。
这是课程数值分析的作业,可能写的有些简陋,希望对读者能够有一些帮助。










