数据结构与算法-栈和队列小练习
这里给大家分享一道栈的练习和一道队列的练习!
1.练习一
利用栈的基本操作实现将任何一个十进制整数转化为R进制整数。
1.1栈的初始化
Sqstack::Sqstack()
{
base = top = new SElemType[InitStacksize];
stacksize = InitStacksize;
}
1.2入栈操作
void Sqstack::push(SElemType e)
{
if (top - base == stacksize)
{
SElemType* base1 = new SElemType[stacksize + increment];
int i = 0;
for (i = 0; i < InitStacksize; i++)
{
base1[i] = base[i];
}
delete[]base;
base = base1;
top = base + stacksize;
stacksize += increment;
}
*top++ = e;
}
1.3出栈操作
SElemType Sqstack::pop()
{
if (base == top)
throw runtime_error("栈为空!");
return *(--top);
}
bool Sqstack::isEmpty()
{
if (base == top)
return 1;
else
return 0;
}
1.4销毁栈
~Sqstack()
{
delete[]base;
stacksize = 0;
}
1.5进制转换函数
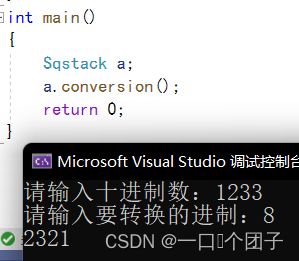
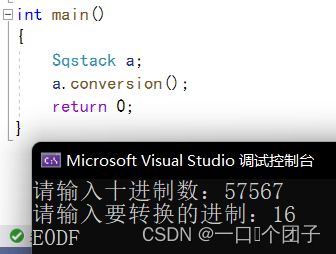
void Sqstack::conversion()
{
long int n = 0;
cout << "请输入十进制数:";
cin >> n;
SElemType b = 0;
cout << "请输入要转换的进制:";
cin >> b;
Sqstack s;
SElemType e;
char a = 'A';
while (n)
{
e = n % b;
s.push(e);
n /= b;
}
while (!s.isEmpty())
{
e = s.pop();
if (e >= 10)
{
a = 'A';
a = a + e - 10;
cout << a;
}
else
{
cout << e;
}
}
cout << endl;
}
1.6判空函数
bool Sqstack::isEmpty()
{
if (base == top)
return 1;
else
return 0;
}
1.7全部代码
#define _CRT_SECURE_NO_WARNINGS 1
#include 2.练习二
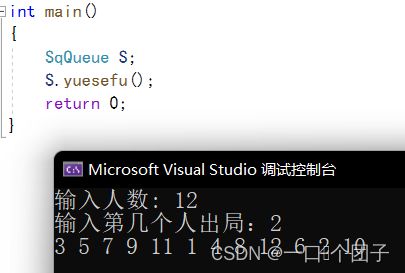
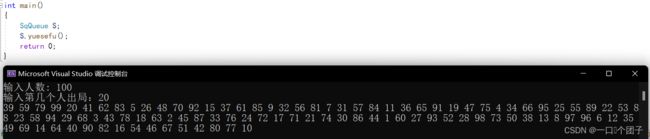
利用循环队列实现.约瑟夫环问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。
从编号为k的人开始报数,数到k的那个人出圈;他的下一个人又从1开始报数,数到k的那个人出圈;
依此规律重复下去,直到圆桌周围的人只剩最后一个。模拟该游戏,并输出出圈顺序。
2.1循环队列初始化
SqQueue::SqQueue()
{
base = new QElemType[QueueSize];
front = rear = 0;
}
2.2队列销毁
~SqQueue()
{
delete[]base;
front = rear = 0;
}
2.3入队操作
void SqQueue::EnQueueu(QElemType e)
{
if (front == (rear + 1) % QueueSize)
return;
else
{
base[rear] = e;
rear = (rear + 1) % QueueSize;
}
}
2.4出队操作
void SqQueue::DeQueue()
{
QElemType e;
if (rear == front)
return;
else
{
e = base[front];
front = (front + 1) % QueueSize;
}
}
2.5队列判空
QElemType SqQueue::IsEmpty()
{
if (front == rear)
return 1;
else
return 0;
}
2.6队列长度
QElemType SqQueue::length()
{
return (rear - front + QueueSize) % QueueSize;
}
2.7获取队头元素
QElemType SqQueue::GetHead()
{
if (front == rear)
return 0;
else
return base[front];
}
2.8约瑟夫环函数
void SqQueue::yuesefu()
{
int n = 0, k = 0;
cout << "输入人数: ";
cin >> n;
cout << "输入第几个人出局:";
cin >> k;
SqQueue S;
int i = 0;
for (i = 1; i <= n; i++)
{
S.EnQueueu(i);
}
for (i = 1; i < k; i++)
{
QElemType temp = S.base[S.front];
S.DeQueue();
S.EnQueueu(temp);
}
int count = 1;
while (!S.IsEmpty())
{
if (count < k)
{
QElemType temp = S.base[S.front];
S.DeQueue();
S.EnQueueu(temp);
count++;
}
if (count == k)
{
cout << S.GetHead() << " ";
S.DeQueue();
count = 1;
}
}
cout << endl;
}
2.9全部代码
/*利用循环队列实现.约瑟夫环问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。
从编号为k的人开始报数,数到k的那个人出圈;他的下一个人又从1开始报数,数到k的那个人出圈;
依此规律重复下去,直到圆桌周围的人只剩最后一个。模拟该游戏,并输出出圈顺序。*/
#define _CRT_SECURE_NO_WARNINGS 1
#define QueueSize 100
#include 好啦,关于栈和队列的小练习到这里就结束啦,后期会继续更新数据结构与算法的相关知识,欢迎大家持续关注、点赞和评论!❤️❤️❤️