
目录
前言
AVL树
1. AVL树的概念和性质
2. AVL树类的属性
3. AVL树的插入函数
4. 总结
红黑树
1. 红黑树的概念和性质(什么是红黑树,并且作为一颗红黑树的要求)
2. 红黑树类的属性
3. 红黑树的插入函数
4. 总结
前言
对于之前普通的二叉搜索树,其搜索的效率依靠树的形状来决定,如下:

可以看到 A图 中的树比较彭亨,搜索一个元素的效率接近 O(logN) ;而 B图 中的形状也符合搜索二叉树,但是很不平衡,这时的搜索效率就变成 O(N) 了(如搜索值为4的节点)
可以看到,如果搜索二叉树不平衡,他的搜索的效率不确定,在 O(logN) 和 O(N) 之间,可能有暴击;
那么对此,既然不平衡,那我们就给出平衡的两种方法:
1.构成AVL树
2.构成红黑树
这两种方法都是为了平衡搜索二叉树而生
AVL树
1. AVL树的概念和性质
它的出现是为了 搜索二叉树的平衡,那就来了解AVL树的概念和性质,也就是什么是AVL,并且作为一颗AVL树的要求是什么
首先AVL树是一颗树,它要求任何一个节点的左右子树的高度差不超过一,以此来保证平衡,是AVL树的核心
来看看它的做法
与搜索二叉树不同,它将二叉链,变成了三叉链(多了指向父节点的指针),并且引入了平衡因子这个东西;这些都是为了方便并且为了树的一个平衡引入
三叉链和平衡因子和下面AVL树属性的图结合起来看更直观
三叉链也就是多了一个 parent指针 指向该节点的父节点,这一操作可以让节点找到其祖先
平衡因子是指该节点的 右子树高度 减去 左子树高度的值,而根据AVL树的性质(要求任何一个节点的左右子树的高度差不超过一),也就是平衡因子 _bf 的值域为 { -1, 0, 1 } ,如果平衡因子 _bf 的值出现为 2 或者 -2 ,说明该树已经不平衡,此时需要进行停止调整,先进行旋转操作
2. AVL树类的属性
这里的节点值类型简化为了int类型,原为 pair


3. AVL树的插入函数
而AVL树的重点呢,也就是AVL树是如何让树达到平衡的呢?就是每插入了一个节点后,进行了一些调整,如果插入节点后不平衡,那么会将其调整成平衡
插入后对插入节点祖先的平衡因子进行调整,当调整过程中,有平衡因子出现异常时,此时通过旋转的方式,让树继续保持平衡
当平衡因子出现异常即是 平衡因子的值更新为 2 或者 -2 时,说明树现在已经不平衡,需要进行旋转
分情况讨论:

现在平衡因子已经出现了不平衡,为什么旋转之后,树就可以继续平衡呢?
具体看到旋转 (这里以左单旋为例):
定义节点指针 parent(图中的节点值为30), cur(图中的60)
左单旋是将 cur 的左孩子给给 parent 的右, 再把 parent 赋值给 cur 的左,旋转完成
再进行平衡因子的更新:parent 和 cur 的平衡因子 _bf 都变成 0

左单旋具体代码如下:
void RotateL(Node* parent)
{
assert(parent);
Node* cur = parent->_right;
Node* cur_left = cur->_left;
// 改变节点之间的关系
parent->_right = cur_left;
cur->_left = parent;
// 改变_parent的指向
//原本 parent 的 _parent
Node* ppNode = parent->_parent;
//若原本 ppNode(原本 parent 的 _parent)为空,说明parent原本不是根,现需把 ppNode 给到 cur 的 _parent,并且把 ppNode 的子更新为 cur
if (ppNode)
{
if (ppNode->_left == parent)
{
ppNode->_left = cur;
}
else
{
ppNode->_right = cur;
}
cur->_parent = ppNode;
}
//若原本 parent->_parent 为空,说明parent原本是根,现需把_root更新为根
else
{
_root = cur;
cur->_parent = nullptr;
}
if (cur_left)
{
cur_left->_parent = parent;
}
parent->_parent = cur;
// 更新平衡因子
cur->_bf = parent->_bf = 0;
}
对左单旋的总结是:当不平衡的树进行左单旋之后,树又被调整为平衡,然后再进行平衡因子的更新
那么右单旋的思路是一样的,自己可以进行推理
而要进行双旋时候,可以再进行讨论(这里以右左旋进行讨论):

右左旋:定义 parent(下图节点值为30), cur(下图节点值为90), cur_left(下图节点值为60)
双旋都是两大步,这里右左旋就是先进行右旋,再进行左旋,旋转结束;对,这里对刚刚实现的单旋代码进行了复用,复用yyds
具体是对 cur 先进行右旋,再对 parent 进行左旋,如下
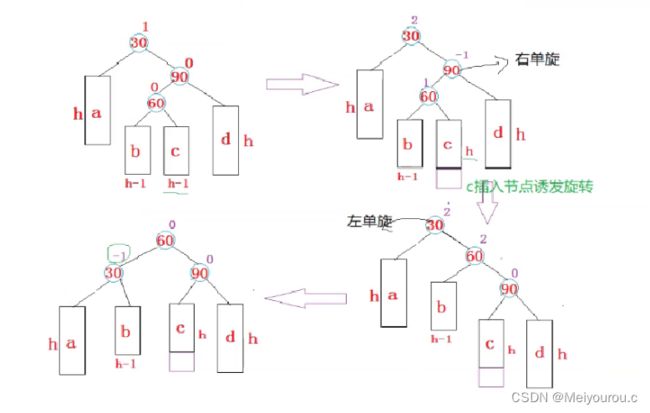
最后进行平衡因子的调整,但是这里特别容易忘记第三种情况的讨论,AVL树的这个细节得注意:

右左旋的代码如下:
void RotateRL(Node* parent)
{
Node* cur = parent->_right;
Node* cur_left = cur->_left;
int bf = cur_left->_bf;
RotateR(parent->_right);
RotateL(parent);
parent->_bf = 0;
cur->_bf = 0;
cur_left->_bf = 0;
if (bf == -1)
{
cur->_bf = 1;
}
if (bf == 1)
{
parent->_bf = -1;
}
}
那么左右旋的思路是一样的,自己可以进行推理
4. 总结
而进行何种旋转本质是取决于 parent cur 和 cur_left (或cur_right)之间的关系,若他们三个所连成的是直线,那么进行单旋操作,如果为折线,那就进行双旋操作;而这里的平衡因子刚好可以体现他们之间的关系,所以上图中根据平衡因子来决定单双旋和左右旋转
AVL树构造和插入函数,测试函数:
这里的节点值类型简化为了int类型,原为 pair
#pragma once
#include
using namespace std;
#include
#include
#include
#include
#include
红黑树
1. 红黑树的概念和性质(什么是红黑树,并且作为一颗红黑树的要求)

以上是红黑树的概念和性质,在红黑树里不仅仅要考虑 cur 、curleft 、 parent 还要引入 grandfather,具体为什么看到后面就知道了
2. 红黑树类的属性
是使用枚举枚举出 红 黑 两种情况
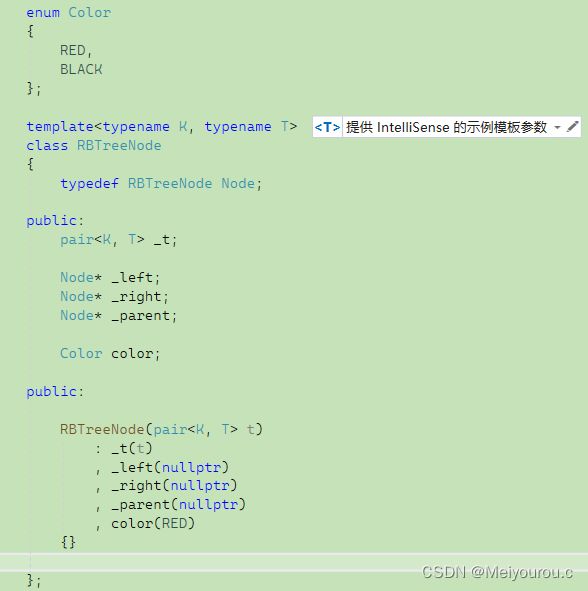
3. 红黑树的插入函数
还是分情况讨论:

4. 总结
根据性质可以分为以下情况:
可以看出第一种情况(uncle存在且为黑)只需要变色即可,在看是否继续向上调整
第二种情况就要旋转了,而如何旋转本质图中也详细说了,取决于 grandfather、parent、cur 之间的关系,其实AVL树的旋转的决定因素也在此,只是转换成平衡因子进行描述
关于红黑,具体的思想关键体现在插入函数中,复习请自行分析出两种大情况,和情况二的细分,然后写出插入函数,才算过关
总体代码:
#pragma once
#include
using namespace std;
#include
#include
#include
#include
#include











