机器学习-各类学习器评价指标

一、各类学习器评价指标

机器学习是借助算法模型来解析数据，并从中学习，然后对真实世界中事件作出决策或预测的方法。根据是否提供数据的分类结果（数据的标签），可将机器学习方法分为两大类：监督学习（如分类和回归方法），无监督学习（如聚类方法）。
在利用机器学习方法对问题作出决策和预测后，我们需要对结果进行评价，此时我们应选择合适的评价指标，不同的学习器相应的指标体系也有差异：
分类模型：准确率、ROC-AUC、混淆矩阵及其相关的一系列指标；
回归模型：误差平方和以及决定系数R2等；
聚类算法：(Given Label)准确率、兰德指数、互信息等，(Not Given Label)紧密性，间隔性，邓恩指数等。

二、分类模型评价指标

2.1混淆矩阵

这里只要记住True、False描述的是分类器是否判断正确，Positive、Negative是分类器的分类结果。

• TP（true positive）：表示样本的真实类别为正，最后预测得到的结果也为正；
• TN（true negative）：表示样本的真实类别为负，最后预测得到的结果也为负；
• FP（false positive）：表示样本的真实类别为负，最后预测得到的结果却为正；
• FN（false negative）：表示样本的真实类别为正，最后预测得到的结果却为负。

根据以上几个指标，可以分别计算出Accuracy、Precision、Recall（Sensitivity，SN），Specificity（SP）。

P(实际为正例)=TP+FN;
N(实际为负例)=TN+FP

• Accuracy：表示预测结果的精确度，预测正确的样本数除以总样本数，accuracy = （TP+TN）/(P+N)。
• Precision，准确率（查准率），表示预测结果中，预测为正样本的样本中，正确预测为正样本的概率，precision=TP/（TP+FP）；
• Recall，召回率（查全率），表示在原始样本的正样本中，最后被正确预测为正样本的概率，recall=TP/(TP+FN)=TP/P；
• Specificity，常常称作特异性，它研究的样本集是原始样本中的负样本，表示的是在这些负样本中最后被正确预测为负样本的概率，specificity = TN/N。

关于Accuracy和Recall两个指标比较：以地震预测为例，没有谁能准确预测地震的发生，但我们能容忍一定程度的误报，假设1000次预测中，有5次预测为发现地震，其中一次真的发生了地震，而其他4次为误报，那么正确率从原来的999/1000=99.9%下降到996/1000=99.6，但召回率从0/1=0%上升为1/1=100%，这样虽然谎报了几次地震，但真的地震来临时，我们没有错过，这样的分类器才是我们想要的，在一定正确率的前提下，我们要求分类器的召回率尽可能的高。

2.2 ROC曲线
ROC受试者工作特征曲线（receiver operating characteristic）亦称感受性曲线(sensitivity curve)，平面的横坐标是false positive rate(FPR)假正率，纵坐标是true positive rate(TPR)真正率。ROC计算过程如下：

1. 给定 m+个正例和 n-个反例，根据学习器预测结果（score）对样例进行排序，然后将分类阈值设置为最大，即所有样例均预测为反例，此时真正例率和假正例率均为0，即在坐标（0,0）处标记一个点；
2. 然后，将分类阈值依次设为每个样例的预测值，即依次将每个样例划分为正例。设前一个标记点坐标为 (x,y)
   ，当前若为真正例，则对应标记点坐标为
   
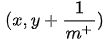
   若当前为假正例，则对应标记点坐标为
   
   然后用线段连接相邻点即得。
   
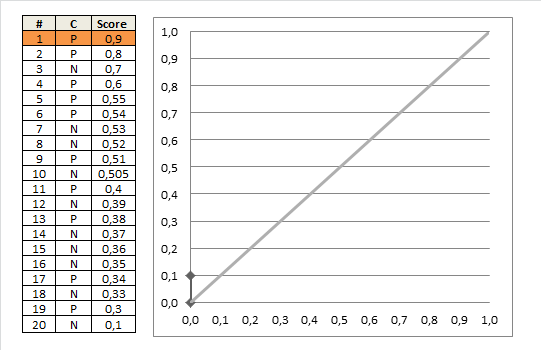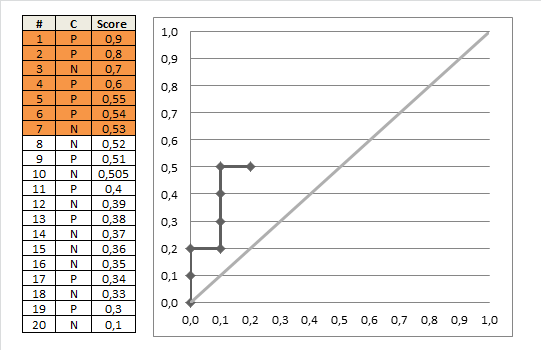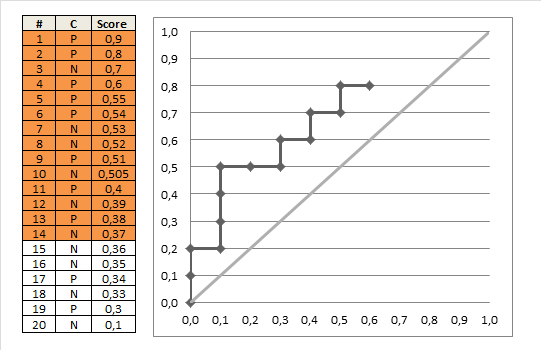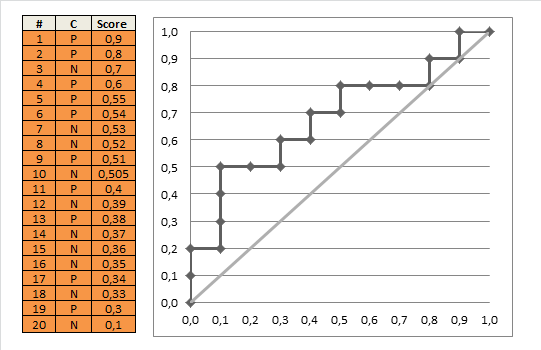
   ROC曲线作用

• 有助于选择最佳阈值：ROC曲线越靠近左上角，模型查全率越高，最靠近左上角的ROC曲线上的点是分类错误最少的最好阈值，其假正例和假反例总数最少；
• 可以比较不同学习器的性能：将各个学习器的ROC曲线绘制在同一坐标中，直观比较，越靠近左上角的ROC曲线代表的学习器准确性越高。

2.3 AUC值
AUC（area under the curve）即ROC曲线下方的面积，取值在0.5到1之间，因为随机猜测的AUC就是0.5。面积如下图所示，阴影部分即为AUC面积，AUC越大，诊断准确性越高。

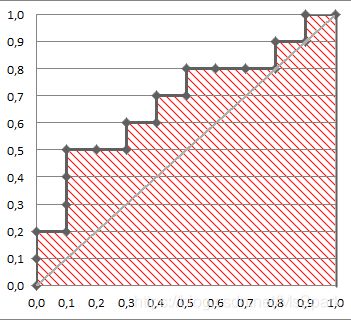
三、回归模型评价指标

3.1 SSE（误差平方和）
观测值与预估值的离差平方和，计算公式为：

同样的数据集的情况下，SSE越小，误差越小，模型效果越好。
缺点：
SSE数值大小本身没有意义，随着样本增加，SSE必然增加，也就是说，不同的数据集的情况下，SSE比较没有意义。

3.2 决定系数R-square
回归平方和与总平方和的商，评估得到的回归方程是否较好拟合样本数据的统计量。
总平方和：

三个平方和之间关系：

决定系数：
或

分母理解为原始数据的离散程度，分子为预测数据和原始数据的误差，二者相除可以消除原始数据离散程度的影响。

决定系数与相关系数对比：

• 决定系数表示回归线拟合程度，即有多少百分比的y波动可以被回归线描述；相关系数表示变量间的相关关系。
• 决定系数大小：R平方越高，回归模型越精确，取值为[0,1]；相关系数等于 (相关性方向符号+or-)决定系数开方，取值为[-1,1]。
• 决定系数越大则拟合优度越好，但具体问题要具体分析；相关系数绝对值越大说明变量相关性越强。

缺点：
数据集的样本越大，R²越大，因此，不同数据集的模型结果比较会有一定的误差。

3.3 校正决定系数Adjusted R-Square
消除了样本数量和特征数量的影响。

n为样本数量，p为特征数量。

四、聚类算法评价指标

根据是否提供数据标签，将模型评价指标分两类：
4.1 Not Given Label
4.1.1 Compactness（CP紧密性）
计算每一个类中各点到聚类中心的平均距离。

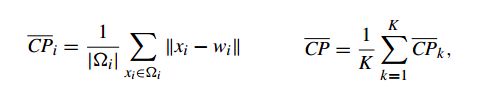
CP越小说明类内聚类聚类越近
缺点： 没有考虑类间效果

4.1.2 Separation（SP间隔性）
计算各聚类中心两两之间平均距离。

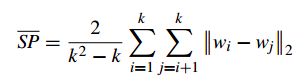
SP越高说明类间距离越远
缺点： 未考虑类内效果

4.1.3 Davies-Bouldin Index（DB分类适确性指标）
任意两类别的类内距离平均距离(CP)之和除以两聚类中心聚类，求最大值。

DB越小越好，说明类内距离小，同时类间距离大
缺点： 因使用欧式聚类，因此对于环状分布的聚类评估较差。

4.2 Given Label
4.2.1 Cluster Accuracy（CA准确度）
计算聚类正确的百分比

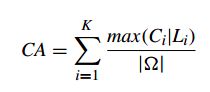
此外还有Rand index（RI兰德系数）、Normalized Mutual Information（NMI标准互信息）等指标可以衡量聚类结果与真实情况的吻合程度。

参考：
https://blog.csdn.net/weixin_39541558/article/details/80705006；
https://blog.csdn.net/Dream_angel_Z/article/details/50867951；
https://blog.csdn.net/liuliuzi_hz/article/details/53909436；
https://zhuanlan.zhihu.com/p/48981694；
https://zhuanlan.zhihu.com/p/48266768；
https://blog.csdn.net/sinat_33363493/article/details/52496011