一文带你搞懂二叉树

目录

一、什么是二叉树

二、创建二叉树

1）二叉树的结构：

2）创建二叉树：

三、二叉树的遍历方式

1）前序遍历：

2）中序遍历：

3）后序遍历：

4）还原二叉树 ：

5）层序遍历：

 四、二叉树的基本操作：

1）二叉树节点个数：

2）二叉树叶子节点个数：

3）二叉树第K层节点个数：

4）二叉树查值：

5）判断是否为完全二叉树：

---

一、什么是二叉树

        二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分。

        二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点————百度百科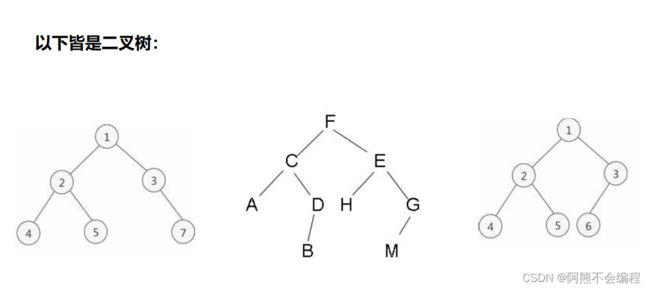

二叉树的最上层也就是第一层（也可以认为是第0层）为根节点(root)，二叉树如其名，每个节点都有对应的左孩子和右孩子，只不过有些孩子为NULL ，也就是说每个节点最多有两个孩子的树为二叉树(Binary Tree)。

        二叉树还可以再细分，其中有两种常见结构，一种是满二叉树(Full Binary Tree)，一种是完全二叉树(Compelete Binary Tree)。

满二叉树：

        除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的深度为K，且结点总数是(2^k) -1 ，则它就是满二叉树。

完全二叉树：

        一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

以下则为几种不同的二叉树结构实例： 

接下来，我们学习以下如何创建一颗二叉树。

---

二、创建二叉树

1）二叉树的结构：

        二叉树的一个个孩子其实就是节点，这个节点存放着左孩子和右孩子的信息，以及节点所存放的数据。知道以上信息我们就可以定义出二叉树的结构了：

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;//每个节点所存储的信息
	struct BinaryTreeNode* left;//左孩子
	struct BinaryTreeNode* right;//右孩子
}BTNode;

        其实我们前面学习的链表也可以看作二叉树，只不过是一个特殊的二叉树，每个节点最多只有一个子孩子不为NULL的二叉树，所以结构上看着与前面的链表相似。 

2）创建二叉树：

        二叉树的创建与前面学习的链表与顺序表都不同，当然你可以采用手动连接成一颗二叉树，但是今天我们要介绍的是递归式生成二叉树。

        首先，假设有这样一颗二叉树：             

这里'#'代表NULL，其他字符就代表节点的数据，那么构建的方式就是用二叉树最常用的构建方式（root——left——right）方式来递归构建，这种方式为前序遍历，我们稍后会提到。

下面为递归创建二叉树的代码：

BTNode* BinaryTreeCreate(BTDataType* a, int* pi)//传入的数组保存着节点的数据，指针pi用来索引数组的下标
{
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));//创建二叉树的当前节点
	root->left = root->right = NULL;//将左右子树置空
	if (a[(*pi)] == '#')//'#'代表NULL指针，遇到空指针直接返回NULL
	{
		(*pi)++;
		return NULL;
	}
	root->data = a[(*pi)++];//存储二叉树节点的数据
    //由 根--左--右 的递归方式构建二叉树
	root->left = BinaryTreeCreate(a, pi);//左孩子接收左子树返回值
	root->right = BinaryTreeCreate(a, pi);//右孩子接收右孩子返回值
	return root;//返回上一节点
}

在这里我们有必要理解递归构建二叉树的过程：        下面我来讲解一下如何进行递归的，最好边看图边理解递归：

        根据上面的代码，首先生成节点A，对A（右子树还未递归）进行左路递归，进入到下一层左孩子不为空构建B（右子树还未递归）。

        B向左孩子递归，左孩子不为空构建D，D在进行递归，递归到左孩子为NULL，则继续进行右路递归，发现右孩子也为NULL,这时候这个节点已经递归完毕，返回上一个节点B。

        此时B的左路递归结束，进行右路递归，右路递归不为NULL，生成节点E。

        E节点继续左路递归发现左路为NULL,则左路结束进行右路递归，右子树不为空，生成节点H,节点H向左递归左路为NULL,进行右路递归，右路为NULL，递归结束，返回到节点E。

        此时节点E也递归结束，返回到节点B，节点B的右路递归也结束，返回到根节点A的左子树部分，此时A的左子树部分递归完毕，向右子树递归，右子树的递归和前面相同方式就不多说了。

---

三、二叉树的遍历方式

        我们已经了解了二叉树的几种结构了，但是请来思考一下这种数据结构，二叉树是用来存储数据的，我们该怎样拿到对应的数据呢？怎样知道自己数据存储是不是对的呢？既然要存储数据，那么遍历一定是少不了的，二叉树的遍历方式与顺序表，链表其实是不同的，接下来我们来学习一下二叉树的遍历方式。

        首先，二叉树的遍历方式是使用递归来完成的，我们前面提到了前序遍历，没错，前序遍历就是一种遍历二叉树的方法，除此以外，遍历二叉树的常用方法还有：中序遍历，后序遍历，层序遍历（也叫广度优先遍历Breadth First Search，简称BFS）。

        中序遍历和后序遍历与前序遍历相似这里就不在展示了，顾名思义，层序遍历而其中层序遍历需要用到栈的数据结构，每次需要根节点的左右子节点依次入栈，这里并不是递归的过程，直到全部入栈，最后输出就为层序遍历的结果。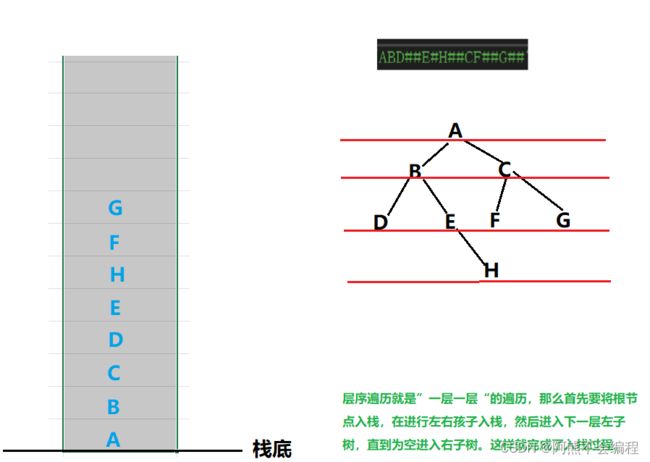

1）前序遍历：

void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
		return;
	printf("%c ", root->data);//前序按照根左右方式遍历，这里的根就是直接打印出来
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
	return;
}

2）中序遍历：

void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
		return;
	BinaryTreeInOrder(root->left);
	printf("%c ", root->data);//中序遍历就是左根右方式遍历
	BinaryTreeInOrder(root->right);
	return;
}

3）后序遍历：

void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
		return;
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c ", root->data);//后序就是左右根
}

4）还原二叉树 ：

三序遍历结果如下：

        前中后序遍历的结果也只是一串数字，那么怎么判断这几串数是不是二叉树呢？其实很简单，前序遍历的结果一定是符合根左右的，那么根节点一定是第一个数据，知道了根节点的位置，那么中序遍历就可以从节点分成左子树和右子树，很容易就还原出二叉树。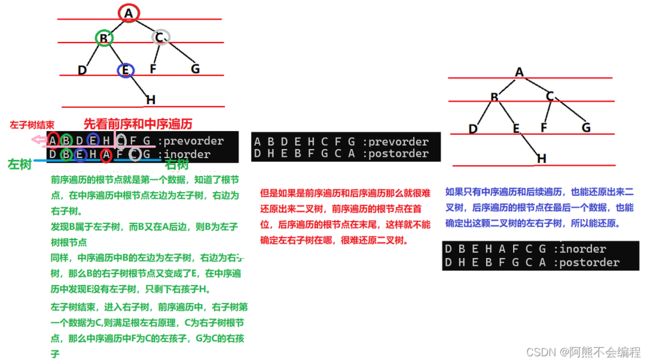

5）层序遍历：

BTNode* stack[MAX_OP];//开辟一个数组表示栈，MAX_OP为20
void BinaryTreeLevelOrder(BTNode* root)
{
	int head, tail;
	head = tail = 0;//这里使用头尾指针进行二叉树元素的索引
	stack[tail++] = root;//首先将根节点入栈，此时将tail+1
	while (head < tail)当头小于尾的时候表示没有全部入栈
	{
		BTNode* node = stack[head++];//把当前节点保存
		if (node->left)//左孩子存在入左孩子
		{
			stack[tail++] = node->left;//入栈
			printf("\t%c -> %c(left)\n", node->data, node->left->data);//将左孩子标注打印
		}
		if (node->right)//右孩子存在入右孩子
		{
			stack[tail++] = node->right;
			printf("\t%c -> %c(right)\n", node->data, node->right->data);//将右孩子标注打印
		}
	}
	return;
}

---

 四、二叉树的基本操作：

        除了二叉树的前中后序遍历和层序遍历外，以下几种二叉树常见用法也给大家来分析一下，以便于更好理解二叉树的递归。

1）二叉树节点个数：

        二叉树的节点个数统计是比较简单的，如果当前点不为空就进行左右递归，每次递归都会记录一个节点，最后返回的值就为节点总数，可以结合着下面的递归展开图来看（红色为向下递的过程，蓝色为往回归的过程）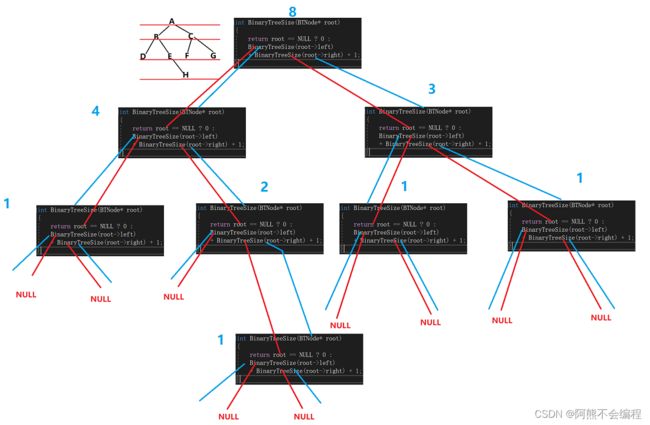

int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;//当前点不为空就进行左右递归，每次递归都会记录一个节点，最后返回的值就为节点总数
}

2）二叉树叶子节点个数：

        二叉树求叶子节点个数就是上面的变形，只需要加上边界条件（左右孩子都为空才为叶子节点）就行了 ，如果还是不太懂就学我上面画出递归展开图，我已经举例了尝试着自己画吧。

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (!root->left && !root->right)//左右孩子都为空才是叶子节点，则返回1
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

3）二叉树第K层节点个数：

        求二叉树的第k层节点，其实也很简单，每次向下递归就-1，直到k为1的时候，表示已经到了该层，就像坐电梯一样会显示你的当前层数，无论你的k为几，你的终点站都是1楼，那么实现起来就简单了，如果还是不太懂，老样子，画出递归展开图就懂了：

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(root);
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

4）二叉树查值：

        这个比较简单，遍历二叉树就行了，不需要多说。

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (!root) return NULL;
	if (root->data == x) return root;

	//单边查找:先左后右
	if (BinaryTreeFind(root->left, x))//如果左边为空则向右查找
		return BinaryTreeFind(root->left, x); //不为空则向下递归查找
	else
		return BinaryTreeFind(root->right, x);
}

5）判断是否为完全二叉树：

        想要判断一棵树是否为完全二叉树，那么首先就得了解完全二叉树的结构，思考一下以什么样的方式可以证明一棵树是完全二叉树？完全二叉树由定义可知，最后一层以上的节点都是满的，而且最后一层节点都是有序的。

        那么只需要这个二叉树全部有序，遍历的过程中间没有空节点，直到遍历到最后一个节点，之后都是空即可，如果中间出现了缺少节点的情况，那么中间一定会出现空节点，空节点后面一定还会有没遍历的节点。

        基于此，使用数据结构中的队列可以完美解决这个问题，先将根节点入队，然后再循环内将左右节点入队，在将根节点出队，当遇到空节点就会停止循环，如果这棵树不是完全二叉树，那么队列中下一个数据就一定不为空，基于此代码如下：

bool BinaryTreeComplete(BTNode* root, int len)
{
	assert(root);
	Que q;
	InitNewQueue(&q);//初始化队列 

	if (root)
	{
		QueuePush(&q, root);//root不为空的话进行入队 
	}

	while (!QueueEmpty(&q))//队列不为空的时候进行入队操作 
	{
		BTNode* front = QueueFront(&q);//队头结点 
		if (front == NULL)
		{
			break;
		}
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
		QueuePop(&q);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}

	QueueDestroy(&q);
	return true;//层序遍历后为连续节点为直接返回true 
}

---

五、二叉树测试 

1）队列信息：

        这里采用的为链式队列：

typedef struct BinaryTreeNode* QDataType;

typedef struct QueueNode {
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue {
	QNode* head;
	QNode* tail;
	int size;
}Que;

//初始化队列  
void InitNewQueue(Que* q)
{
	assert(q);

	q->head = q->tail = NULL;
	q->size = 0;
	return;
}

//入队操作
void QueuePush(Que* q, QDataType x)
{
	assert(q);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc");
		exit(-1);
	}

	newnode->data = x;
	newnode->next = NULL;
	if (q->tail == NULL)
	{
		q->head = q->tail = newnode;
	}
	else
	{
		q->tail->next = newnode;
		q->tail = newnode;
	}

	q->size++;
	return;
}

//出队操作 
void QueuePop(Que* q)
{
	assert(q);
	if (q->head->next == NULL)
	{
		free(q->head);
		q->head = q->tail = NULL;
	}
	else
	{
		QNode* next = q->head->next;
		free(q->head);
		q->head = next;
	}

	q->size -= 1;
	return;
}

//队列判空操作 
bool QueueEmpty(Que* q)
{
	assert(q);
	return q->head == NULL;
}

//取队头元素 
QDataType QueueFront(Que* q)
{
	assert(q);
	assert(!QueueEmpty(q));

	return q->head->data;
}

//取队尾元素 
QDataType QueueBack(Que* q)
{
	assert(q);
	assert(!QueueEmpty(q));

	return q->tail->data;
}

//队列销毁 
void QueueDestroy(Que* q)
{
	assert(q);
	while (q->head)
	{
		QNode* tmp = q->head->next;
		free(q->head);
		q->head = tmp;
	}
	q->head = q->tail = NULL;
	q->size = 0;
	return;
}

2）二叉树操作：

#define MAX_OP 20

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树	000
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->left = root->right = NULL;
	if (a[(*pi)] == '#')
	{
		(*pi)++;
		return NULL;
	}
	root->data = a[(*pi)++];
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a, pi);
	return root;
}

// 二叉树销毁	000
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
	return;
}

// 二叉树节点个数	000
int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

// 二叉树叶子节点个数	000
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (!root->left && !root->right)
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

// 二叉树第k层节点个数	000
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(root);
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	//assert(root);
	if (!root) return NULL;
	if (root->data == x) return root;

	//单边查找:先左后右
	if (BinaryTreeFind(root->left, x))//如果左边为空则向右查找
		return BinaryTreeFind(root->left, x); //不为空则向下递归查找
	else
		return BinaryTreeFind(root->right, x);
}

// 二叉树前序遍历 	000
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
		return;
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
	return;
}

// 二叉树中序遍历	000
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
		return;
	BinaryTreeInOrder(root->left);
	printf("%c ", root->data);
	BinaryTreeInOrder(root->right);
	return;
}

// 二叉树后序遍历	000
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
		return;
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c ", root->data);
}

// 层序遍历（DFS）	000
BTNode* stack[MAX_OP];
void BinaryTreeLevelOrder(BTNode* root)
{
	int head, tail;
	head = tail = 0;
	stack[tail++] = root;
	while (head < tail)
	{
		BTNode* node = stack[head++];
		if (node->left)
		{
			stack[tail++] = node->left;
			printf("\t%c -> %c(left)\n", node->data, node->left->data);
		}
		if (node->right)
		{
			stack[tail++] = node->right;
			printf("\t%c -> %c(right)\n", node->data, node->right->data);
		}
	}
	return;
}

// 判断二叉树是否是完全二叉树
//ABD##E#H##CF##G##
bool BinaryTreeComplete(BTNode* root, int len)
{
	assert(root);
	Que q;
	InitNewQueue(&q);//初始化队列 

	if (root)
	{
		QueuePush(&q, root);//root不为空的话进行入队 
	}

	while (!QueueEmpty(&q))//队列不为空的时候进行入队操作
	{
		BTNode* front = QueueFront(&q);//队头结点
		if (front == NULL)
		{
			break;
		}
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
		QueuePop(&q);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}

	QueueDestroy(&q);
	return true;//层序遍历后为连续节点为直接返回true 
}

3）测试用例：

void Test()
{
	int i = 0;
	//二叉树插入顺序：ABD##E#H##CF##G##
	char a[] = { 'A', 'B', 'D', '#', '#', 'E', '#', 'H', '#', '#', 'C', 'F', '#', '#', 'G', '#', '#', '\0' };
	BTNode* root = BinaryTreeCreate(a, &i);

	BTNode* p = BinaryTreeFind(root, 'B');
	if (p)
	{
		printf("Search: %c is exist\n", p->data);
	}

	BinaryTreePrevOrder(root);	printf(":prevorder\n");
	BinaryTreeInOrder(root);	printf(":inorder\n");
	BinaryTreePostOrder(root);	printf(":postorder\n");

	int len = BinaryTreeSize(root);
	printf("TreeSize :%d\n", len);

	int len2 = BinaryTreeLeafSize(root);
	printf("TreeLeaf :%d\n", len2);

	int len3 = BinaryTreeLevelKSize(root, 2);
	printf("TreeLeve :%d\n", len3);

	BinaryTreeLevelOrder(root);

	return;
}

void TestCompeleteBinaryTree()
{
	int i = 0;
	char a[] = { 'A', 'B', 'D', '#', '#', 'E', '#', 'H', '#', '#', 'C', 'F', '#', '#', 'G', '#', '#', '\0' };

	BTNode* root = BinaryTreeCreate(a, &i);
	int len = BinaryTreeSize(root);

	if (BinaryTreeComplete(root, len))
	{
		printf("It's a complete binary tree.\n");
	}
	else
	{
		printf("It's not a complete binary tree.\n");
	}

	return;
}

int main()
{
	Test();//测试二叉树的其他功能 
	TestCompeleteBinaryTree();//测试是否为完全二叉树 
	return 0;
}

结果为： 

如果这篇文章对各位有用的话，还望各位看官多多三连呐~~