数据结构——链式二叉树
作者:几冬雪来
时间:2023年3月29日
内容:数据结构链式二叉树讲解
目录
前言:
二叉树的应用:
1.搜索二叉树:
2.前序,中序,后序遍历:
1.前序遍历:
2.中序遍历:
3.后续遍历:
4.层序遍历:
3.前序遍历,中序遍历,后序遍历的代码:
1.前序遍历代码:
2.中序遍历代码:
3.后序遍历代码:
4.递归调用的函数展开图(二叉树版):
5.求结点的个数:
6.求树的高度:
7.判断某一层结点的个数:
8.代码:
结尾:
前言:
在上一篇博客当中我们学习了由二叉树内容所拓展出来的堆。在堆的板块结束之后,接下来我们将继续进军二叉树,而今天我们就要对二叉树中的重要知识点——链式二叉树的内容进行讲解。
二叉树的应用:
在这一篇博客之前的树和二叉树,我们只是讲解了它们的操作方法等,也就是对它们知识的了解,它们并没有太大的作用。而且今天我们真真正正的了解二叉树在我们日常中的使用。
1.搜索二叉树:
首先我们先来讲解一下二叉树中的——搜索二叉树。搜索二叉树,它顾名思义就是来寻找我们的想要找到的值因此它也被我们称为——排序二叉树。那么它是长什么样的呢?这里我们就将搜索二叉树给画出来。
上面这棵二叉树就是我们的搜索二叉树,它和我们以前学习到的大堆排序和小堆排序的二叉树不一样,第一眼我们并不能看出什么规律,那么排序二叉树它是怎么样运行的呢?
在这里假设我们要查找一个值——17。这里我们的根结点的值是12,如果要查找的值比12要小,这里我们就走左结点,如果值比12大我们则走右结点。接下来第二层也是这样计算,最后就能找到我们想要的值。
从图中可以看出,我们每进行一层计算搜索我们就去掉一半的数,这种方法听起来有点像我们以前所学习的查找方法——二分查找。
那么搜索二叉树和二分查找相比较,它们谁查找值更加的轻松呢?在学习二分查找的知识的时候,我们曾经说过,在日常我们要查找一个值的时候极少数用到二分查找,因为它的限制太多了。那么二分查找的限制是什么呢?首先进行二分查找我们必须要有一个足够长的数组来存放我们的值,因为二分查找是用下标来查找的,并且二分查找的数组中的值必须的连续的。
2.前序,中序,后序遍历:
在二叉树中,我们并不学习它的增删查改而是学习它的结构,因为二叉树后面的许多操作与它的结果有关。又因为二叉树和我们之前学习的顺序表,链表不一样,二叉树是非线性结构,因此这里要对其遍历就有一定的难度。 所以二叉树的遍历又被分为了——前序,中序,后序遍历和层序遍历。
在遍历二叉树的时候,我们不能将它当成一棵单一的树来看待,我们需要将其拆解,分为左子树,右子树和根,当变为空树后则不用再拆解。
1.前序遍历:
前序遍历也被我们称为前/先根遍历,它的遍历顺序是——根,左子树,右子树。既然知道它的遍历的顺序那么下来我们就将其画出来看看。
这就是我们的前序遍历,先从根1开始,一直向下访问左子树并且打印出来,然后再访问右子树。例如这个图,我们就先一路访问左子树,从1直接访问到3,并且将左子树的值打印出来,当3的左子树为空的时候,我们再去访问3的右子树。当3的右子树为空,我们就要向上走,因为3是2的左子树,所以这里我们又要访问2的右子树。为空再返回到根,再访问根的右子树,依次执行下去,直到左右子树都为空的时候,结束程序。
2.中序遍历:
讲解完了前序接下来我们就来说一说中序遍历。它的遍历方法和前序遍历的方法一样,只不过遍历的顺序有些不同,那么这里的中序遍历的图是怎么样的呢?
这里我们的遍历的顺序是——左子树,根,右子树。可以看出来,一开始我们就直接访问左结点到3,然后访问3的左子树,为空的话则回到3,将3打印出来后再访问它的右子树,如果为空我们就来到2这个根节点,将2打印出来后再去访问2的右子树,依次这样执行。
3.后续遍历:
接下来就剩下我们最后一个遍历方法——后序遍历了,它的执行顺序为——左结点,右结点,根。照旧我们将它的图像给画出来。
这里我们还是先访问到3这个点,然后接下来先访问3的左子树,为空就再访问3的右子树,如果右子树也为空的话我们再打印3这个值。2这个点也是相同的,也因为左子树为3我们已经处理好了,接下来就直接访问它的右子树再打印2这个值就行了。到了1这个根节点我们也不打印,要先处理它的右子树,最后再搞定这个根节点。
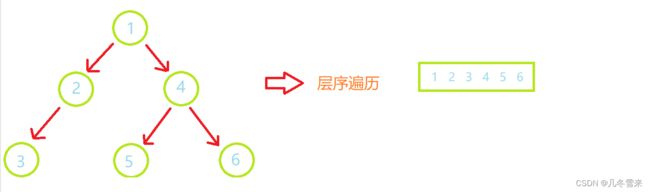
4.层序遍历:
先比较于上面这三种遍历方法,层序遍历就异常简单。它也没有什么顺序可言,这里的层序遍历我们就不对其过多讲解。
这里就是我们这里的层序遍历,十分的简单。
3.前序遍历,中序遍历,后序遍历的代码:
在这里我们既然知道了三种遍历方法是怎么样运行的,那么接下来我们就来书写它们的代码来看看有什么区别。
1.前序遍历代码:
首先这里是我们前序遍历的代码。
因为要存放多个数据,所以还是老样子我们要对我们使用的数据来建一个结构体。
这里简单明了,因为是二叉树所以在这里我们要一个整形来保存我们要输入的值,并且还要有两个指针来指向它的左右子树。
接下来创建一个main函数来存放我们需要调用的另外两个函数,接下来我们就先进去到第一个函数中。
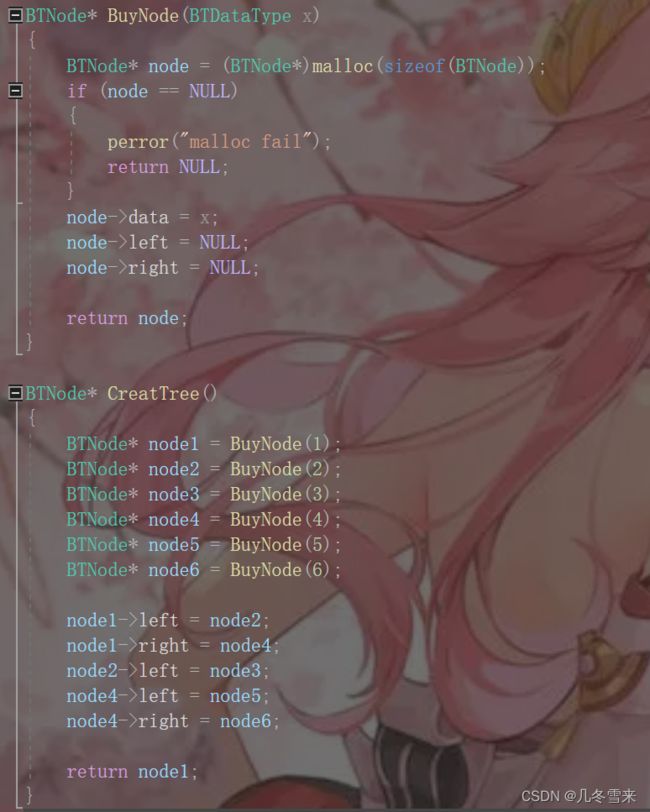
因为要存放值所以要对我们存放的值开辟一块空间,这里也是用的malloc函数来进行开辟。data存放我们要打印的值,左结点和右结点都置为空。接下来就是输入我们存放的数据,这里我们就输入6个数据,然后调整每个根的左右结点的指向。
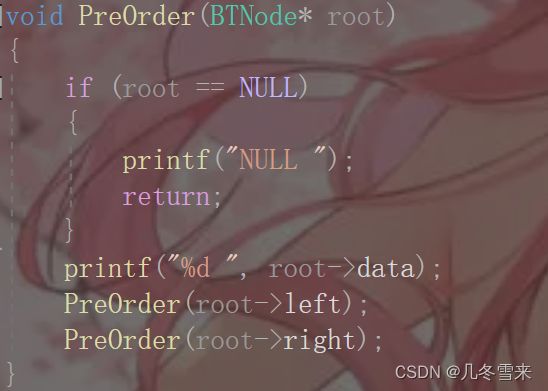
接下来就是打印代码的环节。先打印我们该结点的值,然后再自己调用自己的左子树,类似一个递归的结构,如果root为空则跳出该次root->left的函数调用,然后执行root->right的调用自己的函数。(这里作者表达的可能不太好)
这里结果也符合我们前序排序时所预想的结果。
2.中序遍历代码:
接下来就是我们的中序遍历的代码了,因为有了前序遍历的代码,在这里我们中序遍历的代码只用在它的基础上稍微修改一下即可。
这里需要修改的就是我们的顺序。因为中序遍历的顺序是——左子树,根,右子树,这里我们就将代码顺序修改成这个样子就行了。
它的结构也是和我们中序遍历画图时的结果一样。
3.后序遍历代码:
有了前两个代码作为经验,最后的这个后序遍历的代码就不用我们过多的进行讲解。
这里我们就直接将代码和结果放出来就行了。
4.递归调用的函数展开图(二叉树版):
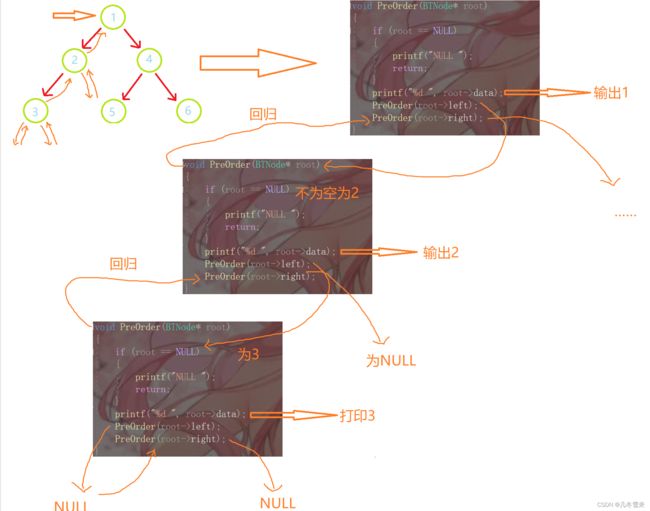
在我们以前学习递归的时候,我们了解到它的本质其实就是不断的建立栈帧。这里我们就来先以前序遍历来画我们的图。
这里的图画起来就是这个样子的,就是一种递归的形式。(右边画布不够所以没画出来) 这里我们的中序遍历亦是如此,这里我们就画一个简略版本的。
而在这个过程中,我们就用到了栈帧的内容,为了不像前序遍历直接打印出数据,在这个过程中我们将1和2这两个值压入栈中。 而这种打印方法则是区别于我们的时机不同,在日常中有些地方就一定要求我们用到前序遍历,不能用其他两种遍历方式。
5.求结点的个数:
那么接下来我们要怎么求出这棵树的结点个数呢?
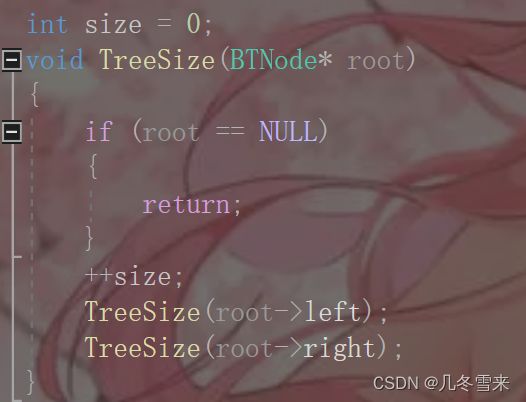
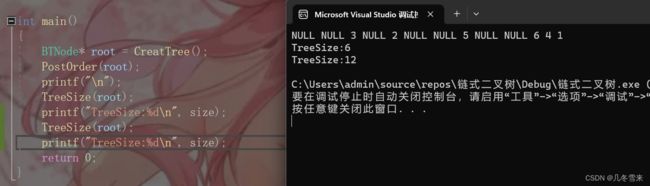
这里我们定义一个全局变量,然后走我们的函数,root指向我们的根结点,如果root为空我们就返回,如果不为空的话我们先对size进行++操作,然后再用类似上方那种递归的操作走完它的左子树和右子树,也就是对它的左子树和右子树进行遍历。
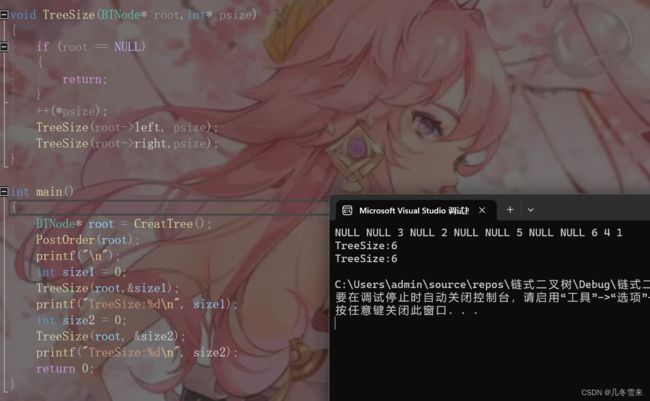
从这里我们可以看出,代码打印了我们想要的结果,但是这里有一个弊端,那就是如果我们再遍历一次代码的话,这里输出的值会从6变为12。所以这里设计一个全局变量的方法不太好,如果要这样写我们就要每次对其进行初始化一次。而且这里也不能使用局部变量来定,最后的方法就是传一个指针变量过去。
但是这种方法还不是我们的最优解。这种方法类似于让我们的根节点依次访问每层结点的个数,那有没有一种方法,就是每个结点保存自己和自己左子树和右子树结点的个数然后返回各自的根,最后再返回给根结点来统计。那当然是有的,接下来我们就将它写出来。
这里就是我们的代码,很明显的是一个三目操作符,那我们来解读一下它是什么意思。首先就是判断是否为空,如果为空就返回0,如果不为空我们就走后面这个式子,这个式子简单来说就是左子树加右子树再加自己本身的结点的总个数。
这里的结果也符合我们预想的结果。
6.求树的高度:
这里我们要来求树的高度,那么树的高度在这里怎么求?
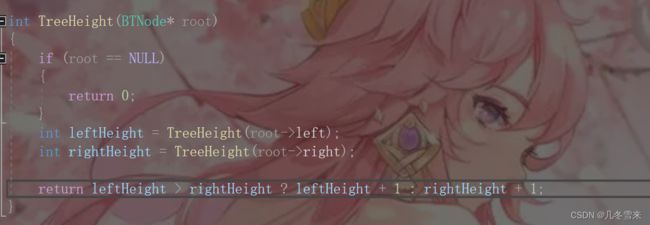
当前树的高度 = 左子树与右子树较大的高度 + 1。
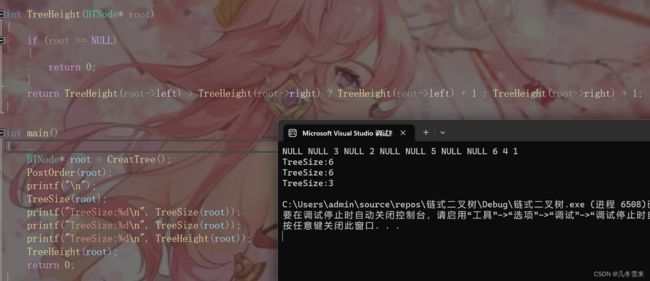
这里我们就进行函数,如果root为空我们就返回0,如果不为空我们就判断左子树和右子树那边比较大,然后执行后序代码递归。结果也是符合我们要求的,但是这个代码有弊端在,它有什么弊端呢?
因为在我们这个代码中,判断与计算是分开的,因此在判断的时候我们就需要遍历一遍代码,在计算的时候又要再遍历一遍。并且在这里我们一直都在实现递归,但是并没有保存我们的地址,因此在执行完了3这个点的判断之后,我们又要从根节点开始到我们再次向下访问,最后一层要走很多次,这里就需要对代码进行改进一下。
这里我们就要将判断和计算分开书写,这里就只需要遍历一次即可来计算它们高度的大小,然后保存在两个整形中,这样子我们就对数据进行了保存,然后再进行判断,因为我们已经计算了它们的高度了,所以这里我们直接对两个整形进行+1即可(根节点) 。这里我们就只需要遍历一次代码,并且每个结点因为被保存过了,所以每一个只需要向下走两次。
7.判断某一层结点的个数:
接下来我们就来计算某一层结点的个数。
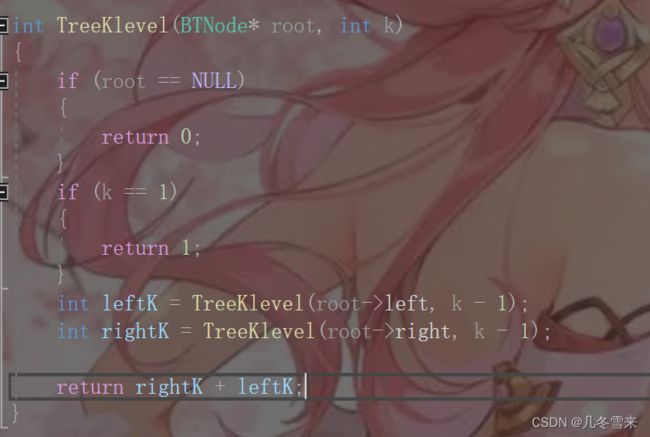
计算某一层结点个数也有我们的公式:某一层结点的个数 = 左子树的第k-1层个数 + 右子树的第k-1层个数。
这里我们可以对其进行一个换算,如果要求第3层的结点个数,如果以根结点为开始,那就是求我们第3层的结点个数,如果从第二层开始,那就是求我们第二层的第二层的结点个数。
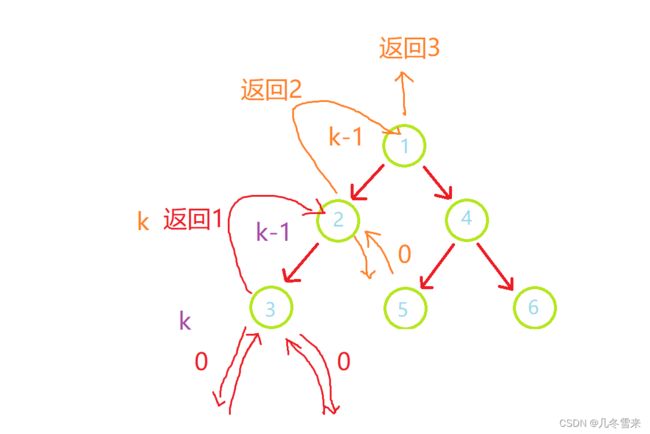
这里就是我们的代码,如果root为空,那就说明我们的树是空树这里就返回0。如果root为1则说明只有一个根节点,这里就返回1,这是两种特别的情况。k-1的话则是访问我们上一层的结点个数,因为要想求第k层的结点个数,首先要先知道第k-1层的结点个数。然后再判断第k层的结点是否为空。
这就是我们的运行步骤。最后我们只需要统计个数即可。
8.代码:
这里到最后我们也将代码全部放上来。
#include
#include
#include
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreatTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
//void TreeSize(BTNode* root,int* psize)
//{
// if (root == NULL)
// {
// return;
// }
// ++(*psize);
// TreeSize(root->left, psize);
// TreeSize(root->right,psize);
//}
//
//int main()
//{
// BTNode* root = CreatTree();
// PostOrder(root);
// printf("\n");
// int size1 = 0;
// TreeSize(root,&size1);
// printf("TreeSize:%d\n", size1);
// int size2 = 0;
// TreeSize(root, &size2);
// printf("TreeSize:%d\n", size2);
// return 0;
//}
int TreeSize(BTNode* root)
{
//左子树加右子树再加自己
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//int TreeHeight(BTNode* root)
//{
// if (root == NULL)
// {
// return 0;
// }
// return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
//}
int TreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
int TreeKlevel(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
int leftK = TreeKlevel(root->left, k - 1);
int rightK = TreeKlevel(root->right, k - 1);
return rightK + leftK;
}
int main()
{
BTNode* root = CreatTree();
PostOrder(root);
printf("\n");
TreeSize(root);
printf("TreeSize:%d\n", TreeSize(root));
printf("TreeSize:%d\n", TreeSize(root));
printf("TreeSize:%d\n", TreeHeight(root));
TreeHeight(root);
return 0;
} 结尾:
到这里,二叉树的内容学习至今,我们已经可以算是半只迈入二叉树的真正核心内容的学习了。二叉树作为我们的一个重要的知识板块,我们还需要多去做题,这样才能进一步提高我们对二叉树的理解。最后希望这篇博客能给大家带来帮助。