数据结构与算法——二叉树与图汇总整理
目录
- 预备知识:二叉树基础知识
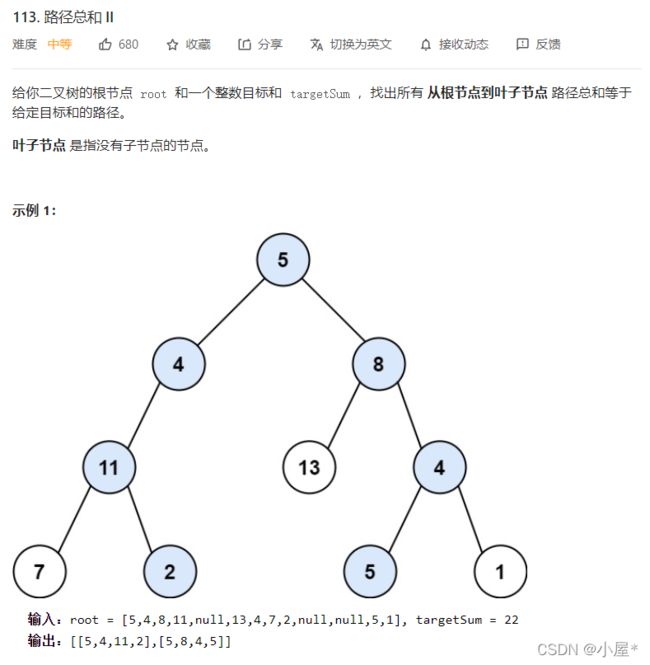
- 例1:路径之和2(medium)(二叉树深搜)
- 例2:最近的公共祖先(medium)(二叉树性质)
- 例3:二叉树转链表(medium)(二叉树与链表)
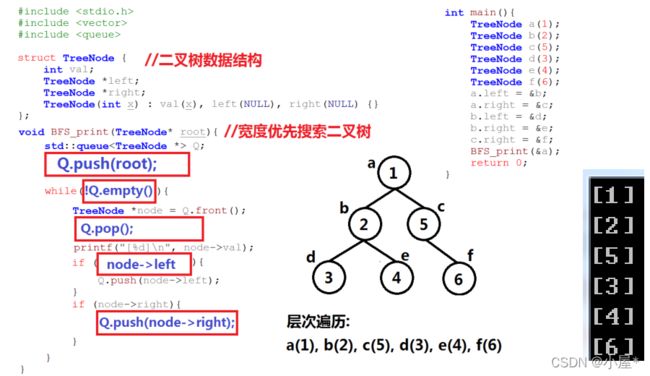
- 预备知识:二叉树层次遍历
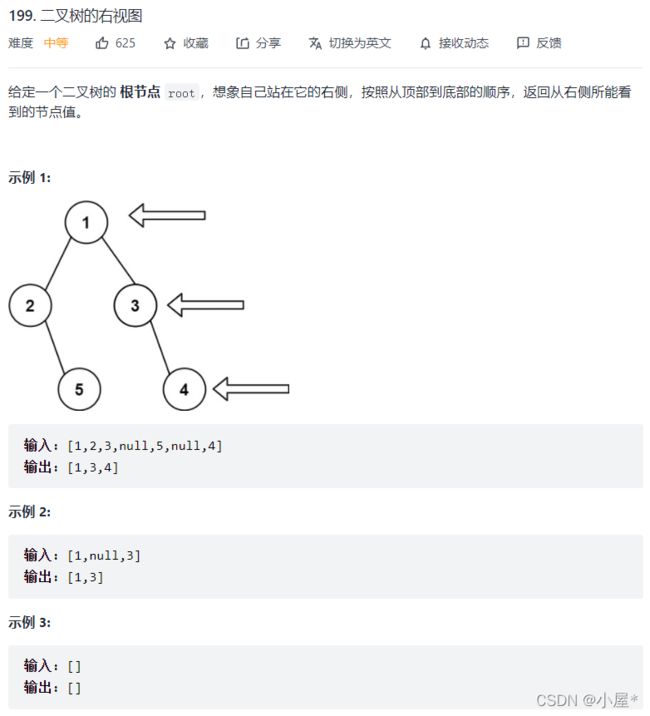
- 例4:侧面观察二叉树(medium)(二叉树宽搜)
- 预备知识:图的基础知识
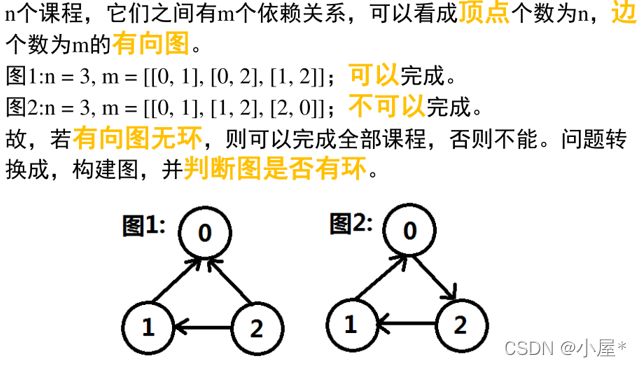
- 例5:课程安排(有向图判断环)(medium)
预备知识:二叉树基础知识
树是n(n>=0)个节点的有限集,且这些节点满足如下关系:
(1)有且仅有一个节点没有父结点,该节点称为树的根。
(2)除根外,其余的每个节点都有且仅有一个父结点。
(3)树中的每一个节点都构成一个以它为根的树。
二叉树在满足树的条件时,满足如下条件:
每个节点最多有两个孩子(子树),这两个子树有左右之分,次序不可颠倒。
遍历:
例1:路径之和2(medium)(二叉树深搜)
class Solution {
public:
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<vector<int>>result;//存储所有满足结果的路径
vector<int>path;//记录单个路径
int path_value = 0;//路径上的总和
preorder(root, targetSum, path_value, path, result);
return result;
}
private:
void preorder(TreeNode* node, int& targetSum, int& path_value, vector<int>& path, vector<vector<int>>& result) {
if (!node) {
return;
}
path_value += node->val;
path.push_back(node->val);
if (!node->left && !node->right && path_value == targetSum) {
result.push_back(path);
}
preorder(node->left, targetSum, path_value, path, result);
preorder(node->right, targetSum, path_value, path, result);
path_value -= node->val;
path.pop_back();
}
};例2:最近的公共祖先(medium)(二叉树性质)
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
vector<TreeNode*>path;//临时栈
vector<TreeNode*>node_p_path;//存储p节点路径
vector<TreeNode*>node_q_path;//存储q节点路径
int finish = 0;
preorder(root, p, path, node_p_path, finish);
path.clear();
finish = 0;
preorder(root, q, path, node_q_path, finish);
int path_len = 0;//记录较短路径的长度
if (node_p_path.size() < node_q_path.size()) {
path_len = node_p_path.size();
}
else {
path_len = node_q_path.size();
}
TreeNode* result = 0;
for (int i = 0; i < path_len; i++) {
if (node_p_path[i] == node_q_path[i]) {
result = node_p_path[i];
}
}
return result;
}
private:
void preorder(
TreeNode* node,//正在遍历的节点
TreeNode* search,//待搜索的节点
vector<TreeNode*>& path,//遍历时的节点路径栈
vector<TreeNode*>& result,//最终搜索到的search路径结果
int& finish//记录是否找到,找到为1未找到为0
) {
if (!node || finish) {
return;
}
path.push_back(node);
if (node == search) {
finish = 1;
result = path;
}
preorder(node->left, search, path, result, finish);
preorder(node->right, search, path, result, finish);
path.pop_back();
}
};例3:二叉树转链表(medium)(二叉树与链表)

方法一:先遍历二叉树,将遍历到的节点存至vector中,最后连接(左节点置空;右节点指向下一元素)
class Solution {
public:
void flatten(TreeNode* root) {
vector<TreeNode*>node_vec;
preorder(root, node_vec);
for (int i = 1; i < node_vec.size(); i++) {
node_vec[i - 1]->left = NULL;
node_vec[i - 1]->right = node_vec[i];
}
}
private:
void preorder(
TreeNode* node, vector<TreeNode*>& node_vec
) {
if (!node) {
return;
}
node_vec.push_back(node);
preorder(node->left, node_vec);
preorder(node->right, node_vec);
}
};class Solution {
public:
void flatten(TreeNode* root) {
TreeNode* last = NULL;
preorder(root, last);
}
private:
void preorder(TreeNode* node, TreeNode*& last) {
if (!node) {
return;
}
//叶节点情况
if (!node->left && !node->right) {
last = node;
return;
}
TreeNode* left = node->left;
TreeNode* right = node->right;
TreeNode* left_last = NULL;
TreeNode* right_last = NULL;
//有左子树
if (left) {
preorder(left, left_last);
node->left = NULL;
node->right = left;
last = left_last;
}
//有右子树
if (right) {
preorder(right, right_last);
if (left_last) {
left_last->right = right;
}
last = right_last;
}
}
};预备知识:二叉树层次遍历
例4:侧面观察二叉树(medium)(二叉树宽搜)
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int>view;
queue<pair<TreeNode*, int>>Q;
if (root) {
Q.push(make_pair(root, 0));
}
while (!Q.empty()) {
TreeNode* node = Q.front().first;
int depth = Q.front().second;
Q.pop();
if (view.size() == depth) {
view.push_back(node->val);
}
else {
view[depth] = node->val;
}
if (node->left) {
Q.push(make_pair(node->left, depth + 1));
}
if (node->right) {
Q.push(make_pair(node->right, depth + 1));
}
}
return view;
}
};预备知识:图的基础知识
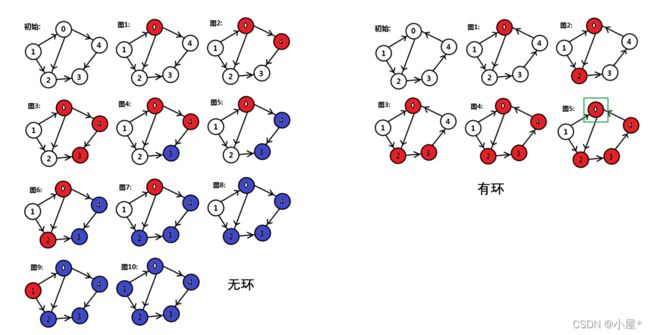
例5:课程安排(有向图判断环)(medium)
struct GraphNode {
int label;
std::vector<GraphNode*> neighbors;
GraphNode(int x) : label(x) {};
};
bool DFS_graph(GraphNode* node, std::vector<int>& visit) {
visit[node->label] = 0;
for (int i = 0; i < node->neighbors.size(); i++) {
if (visit[node->neighbors[i]->label] == -1) {
if (DFS_graph(node->neighbors[i], visit) == 0) {
return false;
}
}
else if (visit[node->neighbors[i]->label] == 0) {
return false;
}
}
visit[node->label] = 1;
return true;
}
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
std::vector<GraphNode*> graph;
std::vector<int> visit;
for (int i = 0; i < numCourses; i++) {
graph.push_back(new GraphNode(i));
visit.push_back(-1);
}
for (int i = 0; i < prerequisites.size(); i++) {
GraphNode* begin = graph[prerequisites[i][1]];
GraphNode* end = graph[prerequisites[i][0]];
begin->neighbors.push_back(end);
}
for (int i = 0; i < graph.size(); i++) {
if (visit[i] == -1 && !DFS_graph(graph[i], visit)) {
return false;
}
}
for (int i = 0; i < numCourses; i++) {
delete graph[i];
}
return true;
}
};struct GraphNode {
int label;
std::vector<GraphNode*> neighbors;
GraphNode(int x) : label(x) {};
};
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
std::vector<GraphNode*> graph;
std::vector<int> degree;
for (int i = 0; i < numCourses; i++) {
degree.push_back(0);
graph.push_back(new GraphNode(i));
}
for (int i = 0; i < prerequisites.size(); i++) {
GraphNode* begin = graph[prerequisites[i][1]];
GraphNode* end = graph[prerequisites[i][0]];
begin->neighbors.push_back(end);
degree[prerequisites[i][0]]++;
}
std::queue<GraphNode*> Q;
for (int i = 0; i < numCourses; i++) {
if (degree[i] == 0) {
Q.push(graph[i]);
}
}
while (!Q.empty()) {
GraphNode* node = Q.front();
Q.pop();
for (int i = 0; i < node->neighbors.size(); i++) {
degree[node->neighbors[i]->label]--;
if (degree[node->neighbors[i]->label] == 0) {
Q.push(node->neighbors[i]);
}
}
}
for (int i = 0; i < graph.size(); i++) {
delete graph[i];
}
for (int i = 0; i < degree.size(); i++) {
if (degree[i]) {
return false;
}
}
return true;
}
};