谱分析：互谱密度

理论

先讲一点儿理论相关的东西，在后面使用matlab实现，加深大家的理解。

功率谱密度

在物理学中，信号通常是波的形式表示，例如电磁波、随机振动或者声波。当波的功率频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）；不要和 spectral power distribution（SPD） 混淆。功率谱密度的单位通常用每赫兹的瓦特数（W/Hz）表示，后者使用波长而不是频率，即每纳米的瓦特数（W/nm）来表示。

计算定义

尽管并非一定要为信号或者它的变量赋予一定的物理量纲，下面的讨论中假设信号在时域内变化。
上面能量谱密度的定义要求信号的傅里叶变换必须存在，也就是说信号平方可积或者平方可加。一个经常更加有用的替换表示是功率谱密度（PSD），它定义了信号或者时间序列的功率如何随频率分布。这里功率可能是实际物理上的功率，或者更经常便于表示抽象的信号被定义为信号数值的平方，也就是当信号的负载为1欧姆(ohm)时的实际功率。此瞬时功率（平均功率的中间值）可表示为：

$$P=S^2(t)$$

由于平均值不为零的信号不是平方可积的，所以在这种情况下就没有傅里叶变换。幸运的是维纳-辛钦定理（Wiener-Khinchin theorem）提供了一个简单的替换方法，如果信号可以看作是平稳随机过程，那么功率谱密度就是信号自相关函数的傅里叶变换。

计算方法

信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程，那么自相关函数一定是两个变量的函数，这样就不存在功率谱密度，但是可以使用类似的技术估计时变谱密度。
f(t) 的谱密度和 f(t) 的自相关组成一个傅里叶变换对（对于功率谱密度和能量谱密度来说，使用着不同的自相关函数定义）。
通常使用傅里叶变换技术估计谱密度，但是也可以使用如Welch法（Welch’s method）和最大熵这样的技术。
傅里叶分析的结果之一就是Parseval（帕塞瓦尔）定理（Parseval’s theorem，其有时也被称为瑞利能量定理，Rayleigh’s energy theorem），这个定理表明函数平方的和（或积分），也就是其能量，等于其傅里叶转换式平方之和（或者积分）：
$${\int }_{-\infty }^{+\infty }|x(t){|}^{2}dt={\int }_{-\infty }^{+\infty }|x(f){|}^{2}df$$
其中 X(f) = F.T. { x(t) } 为x(t) 的连续傅立叶变换，f 是 x 的频率分量。
上面的定理在离散情况下也是成立的 (DTFT 和 DFT)。另外的一个结论是功率谱密度下总的功率与对应的总的平均信号功率相等，它是逐渐趋近于零的自相关函数。

其他定义

功率谱密度谱是一种概率统计方法，是对随机变量均方值的量度。一般用于随机振动分析，连续瞬态响应只能通过概率分布函数进行描述，即出现某水平响应所对应的概率。
功率谱密度的定义是单位频带内的“功率”（均方值）
功率谱密度是结构在随机动态载荷激励下响应的统计结果，是一条功率谱密度值—频率值的关系曲线，其中功率谱密度可以是位移功率谱密度、速度功率谱密度、加速度功率谱密度、力功率谱密度等形式。数学上，功率谱密度值—频率值的关系曲线下的面积就是均方值
，当均值为零时均方值等于方差，即响应标准偏差的平方值。

互谱定义

互谱(cross-power spectrum) 互功率密度谱的简称，在频域内描述两个不同信号之间统计相关程度的一种方法。
设有两个平稳随机信号x(t)与y(t)，根据随机过程理论，它们之间的统计相关特性，应该用其互相关函数表达。对x(t)与y(t)的互相关函数进行傅里叶变换，获得其频域中的功率密度谱，即称为互功率密度谱，也称互频谱。可见，互谱与互相关函数是分别从频域和时域描述两个信号统计相关的两种不同表示，它们互为傅里叶变换。互谱也适用于确定性信号分析。互谱在通信及信号处理领域中有重要用途，可用来测定一个未知参数的线性系统的频率响应。这时主要要测出系统输入和输出信号之间的互谱。互谱也可以用于系统时延，如声纳接收信号等时延估计。
在实用中，通常利用快速傅里叶变换来计算和测量互谱，这是因为实际要求提高测量运算速度而提出来的，已经生产了许多测量功率谱密度函数的仪器，它们也可以用于互谱的测量。
现代谱分析是20世纪70年代发展起来的新兴学科。新的方法、新的软件以及新的VLSI谱分析专用硬件不断出现，并在越来越多的领域中获得成功的应用。在现代谱分析理论和方法的研究中，ARMA参数模型方法和特征分析方法是人们十分关心的研究课题。在参数模型方法中对AR方法的研究比较成熟。虽然从理论上说ARMA方法应当具有比AR方法更优越的性能，但现在还没有有效的ARMA谱估计方法。已经提出的方法不是性能不够理想，就是计算太复杂，距实际应用相差甚远。现代谱估计中的特征分析方法都有优越的谱分析性能。特征方法和子空间理论的研究在阵列信号处理中对提高方位估计的分辨力和估计精度均有重要意义。
由于实际信号的时变、非平稳等复杂情况，研究多种信号的韧性(robust)谱估计，以及研究时变谱估计是谱分析研究的一个重要方面。对于实际应用中经常遇到的如噪声中单个或多个正弦信号的频率估计，窄带信号和宽带信号谱分析，以及淹没在噪声中的信号的谱分析等问题也是今后研究的重要课题。
为了加速现代谱分析方法的实际应用，人们重视快速算法和有效的算法结构的研究，尤其是能够用超大规模集成电路硬件实现的实时谱分析方法。多维谱估计和高阶谱估计的研究受到重视，其中人们十分感兴趣的研究课题是对双谱和三谱估计的研究，可用于估计信号中的相位和描述时间序列的非线性特性等。

互谱密度函数

互谱密度函数(cross-spectral density function)是互相关函数的傅立叶变换。互谱密度函数一般与互相关函数具有同样的应用，但它提供的结果是频率的函数而不是时间的函数。这—事实大大开拓了使用范围，因此在可以应用相关分析的工程问题中大大增加了互谱方法的应用。互谱密度函数是有重要用途的，频谱分析中能用互谱的测量结果来识别动力系统的特性以及计算频响函数的振幅比和相位角

互谱密度函数定义

互谱密度函数的定义，数学上可描述为
$$S_{xy}(f)=\underset{T->\infty }{\lim }\frac{1}{T}[X_T^{\ast }(f)Y_T(f)],-\infty <f<+\infty (1)$$

由于互谱密度函数的推导方法与自谱密度函数相同，它们的差别只是$$S_{xx}$$是信号x(t)的自乘，而$$S_{xy}$$是信号$$x(t),y(t)$$的互乘。应当注意的是，因为$$X_T^{\ast }$$与$$Y_T$$一般不是互为共轭，所以$$S_{xy}$$为复数性质。
互谱的单边谱为
$$G_{xy}(f)=2S_{xy}(f),f\ge 0,0,f<0$$
由式(2)互谱密度函数也可以描述为
$$S_{xy}(f)=\underset{T->\infty }{\lim }\frac{2}{T}[X_T^{\ast }(f)Y_T(f)].$$

总结

自功率谱密度函数Sxx（f）：反映相关函数在时域内表达随机信号自身与其他信号在不同时刻的内在联系。
1、当随机信号均值为零时，自相关函数和自功率谱密度函数互为傅立叶变换对。
2、自功率谱密度有明确的物理含义：当tao＝0时，Sxx（f）曲线与频率轴f所包围的面积就是信号的平均功率。另外，Sxx（f）还表明了信号的功率密度沿频率轴的分布状况，因此称Sxx（f）为自功率谱密度函数。

Matlab 实现

cpsd 使用welch方法计算互功率谱密度

1Pxy=cpsd（X，Y）返回使用welch方法计算的两个离散时间序列信号的互谱功率密度Pxy，
默认参数中，X和Y会被分成八段，每段重复50%，每段通过汉明窗加窗，同时计算八个加权的谱密度并做平均。可以使用“Help pwelch”和“Help cpsd” 来查看完整的细节
X和Y可以是向量或者二维的矩阵。如果它们都是矩阵，他们必须有相同的尺寸。CPSD会按照列的维度计算，即Pxy（：，n）=cpsd（X(:,n),Y(:,n)）.如果其中一个是矩阵另一个是向量的话，这个向量会被转变成一个列向量，并且进行扩展。因此，输入都必须有相同数目的列。
Pxy是单位频率能量的谱分布。对于实信号，cpsd反馈的是单边的互谱密度；对于复数信号，它返回的是双边的互谱密度。注意这里单边的互谱密度包含了输入信号的全部能量。
Pxy=CPSD（X，Y，window），当window是一个向量时，将x和y的每一列分成由Pxy = cpsd(X,Y,WINDOW), 每一块儿的向量长度和窗口数相同的不重合的区域。如果窗口是一个整数，那么每一列会被分割成和window数一样长的区段，每一个区段都会使用汉明窗进行加窗。如果窗口参数是空的，则会将x和y分割成八个区域，并使用汉明窗进行加窗。
Pxy=cpsd（x,y,wiodow,noverlap）使用noverlap参数 控制每个区段之间重复的样本数。
Noverlap 必须是一个小于窗口长度的整数，如果窗口数是一个向量的话。如果是一个标量的话，则必须比窗口小。默认的Noverlap等于50%。
【Pxy，W】=cpsd（x,y,window,noverlap,nfft）确定了用了计算CPSD的FFT的点数。对于每一个实信号，Pxy的长度为（NFFT/2+1），如果NFFT是偶数。如果NFFT是奇数则长度为（NFFT+1）/2.对于复信号，Pxy长度始终为NFFT。如果NFFT被设置为空，则NFFT点数或者是256或者是比x和y大的最小的2的幂。 如果NFFT比每段的数据都长，则会对数据段进行补零操作。如果数据段比NFFT点数大，则会使用wrapped使得数据的长度等于NFFT。这个产生了正确的FFT点数，在NFFT比区段长度短时。W是记载了归一化后psd计算频率点的向量。W是单位角度每样本数。对于实信号，W扩张至【0,pi】这个区间当NFFT点数是偶数的时候，【0，pi）当NFFT是奇数的时候。
对于复数信号，w扩张至【0，2pi）这个区间。
[Pxy,W]=cpsd(X,Y,Window,Noverlap,W)计算在向量w中的标准角度频率存在的双边互谱密度，w必须至少有两个元素。
[Pxy,F]=cpsd(x,Y,window,noverlap,nfft,Fs)返回作为实际频率函数的互谱密度。Fs是用HZ表示的采样频率。如果Hz数没写的话，则默认是1HZ.
F是存储Pxy计算点的频率向量（单位为Hz）。对于实信号，F会扩张到间隔[0,Fs/2]当NFFT
是偶数的时候，扩张到[0,Fs/2),当NFFT是奇数的时候。对于复数信号，F
则扩张至[0,Fs).
[Pxy,F]=cpsd(X,Y,window,noverlap,F，Fs)计算存储在频率向量F中存放的点的互谱密度。F必须使用至少两个元素来表示，单位是HZ
[…]=cpsd(…,Freqrange)返回在特定频率范围计算的互谱密度，使用的参数FREQrange限定的范围。
‘onesided’-返回输入的实信号x和y的单边的互谱密度。如果NFFT是偶数，Pxy的长度为NFFT/2+，计算的间隔为[0,pi].如果NFFT是奇数，Pxy的长度则为(NFFT+1)/2和同时在频率范围[0,pi]计算,当Fs被设置时，间隔为[0,fs/2]或者[0,Fs/2).
‘twosided’-返回双边的互谱密度信号，对于实或者复数的输入信号x和y。Pxy有长度NFFT同时在频率范围[0,2pi)内计算。当Fs被设置时，间隔为[0,Fs）.
‘centered’-返回中心化的双边互谱密度对于实或者复的输入信号x和y。Pxy长度为NFFT同时在间隔(-pi,pi]进行计算。
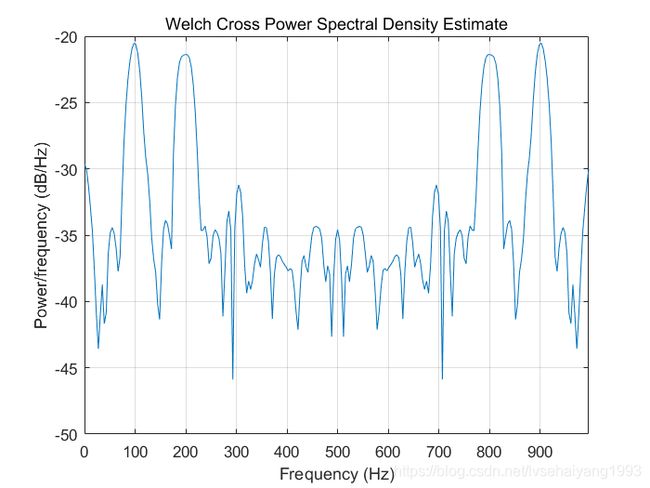
如果不设置输出参数，则画出互谱密度（单位是分贝/每频率）
例子

   Fs = 1000;   t = 0:1/Fs:.296;
       x = cos(2*pi*t*200)+randn(size(t));  % A cosine of 200Hz plus noise
       y = cos(2*pi*t*100)+randn(size(t));  % A cosine of 100Hz plus noise
       cpsd(x,y,[],[],[],Fs,'twosided');    % Uses default window, overlap & NFFT. 

结果如图所示，100Hz有个高峰。