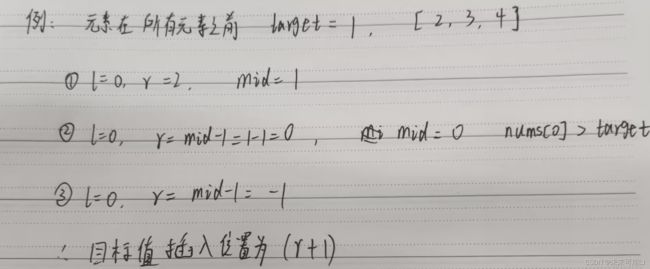力扣刷题【数组篇】
力扣刷题 【数组篇】
文章目录
-
- 力扣刷题 【数组篇】
-
- 一、二分查找
- 二、双指针算法
- 三、模拟题
- 四、总结
一、二分查找
-
第一种写法：左闭右闭的写法，也就是[left, right]
(1) while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
(2) if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target
-
时间复杂度：O（ log n )；空间复杂度：O（1）； 模板代码如下：
// 版本一 class Solution { public: int search(vector<int>& nums, int target) { int left = 0; int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right] while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <= int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2 if (nums[middle] > target) { right = middle - 1; // target 在左区间，所以[left, middle - 1] } else if (nums[middle] < target) { left = middle + 1; // target 在右区间，所以[middle + 1, right] } else { // nums[middle] == target return middle; // 数组中找到目标值，直接返回下标 } } // 未找到目标值 return -1; } };
-
第二种写法：定义 target 是在一个在左闭右开的区间里，也就是[left, right)
- while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle
-
时间复杂度：O（ log n )；空间复杂度：O（1）； 模板代码如下：
// 版本二 class Solution { public: int search(vector<int>& nums, int target) { int left = 0; int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right) while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 < int middle = left + ((right - left) >> 1); if (nums[middle] > target) { right = middle; // target 在左区间，在[left, middle)中 } else if (nums[middle] < target) { left = middle + 1; // target 在右区间，在[middle + 1, right)中 } else { // nums[middle] == target return middle; // 数组中找到目标值，直接返回下标 } } // 未找到目标值 return -1; } };
-
二分习题分析：
（1）搜索插入位置
思路分析：
1> 插入的位置有四种情况，如下图：
- 时间复杂度：O（ log n )；空间复杂度：O（1）； 模板代码如下：
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n - 1; // 定义target在左闭右闭的区间里，[left, right]
while (left <= right) { // 当left==right，区间[left, right]依然有效
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间，所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间，所以[middle + 1, right]
} else { // nums[middle] == target
return middle;
}
}
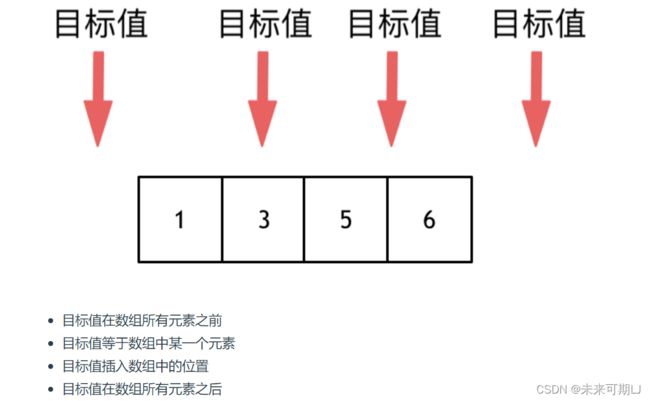
// 分别处理如下四种情况
// 目标值在数组所有元素之前 [0, -1]
// 目标值等于数组中某一个元素 return middle;
// 目标值插入数组中的位置 [left, right]，return right + 1
// 目标值在数组所有元素之后的情况 [left, right]， 因为是右闭区间，所以 return right + 1
return right + 1;
}
};
（2）在排序数组中查找元素的第一个和最后一个位置
思路分析：
- 情况一：arget 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2，此时应该返回{-1, -1}
- 情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
- 情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}
寻找右边界的代码如下：
// 二分查找，寻找target的右边界（不包括target）
// 如果rightBorder为没有被赋值（即target在数组范围的左边，例如数组[3,3]，target为2），为了处理情况一
int getRightBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
while (left <= right) { // 当left==right，区间[left, right]依然有效
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间，所以[left, middle - 1]
} else { // 当nums[middle] == target的时候，更新left，这样才能得到target的右边界
left = middle + 1;
rightBorder = left;
}
}
return rightBorder;
}
二、双指针算法
- 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
（1）移除元素
int removeElement(int* nums, int numsSize, int val){
// 利用双指针的思想
int src = 0, dst = 0; //src 指向原来数组；dst 指向新数组
while (src < numsSize)
{
if (nums[src] == val)
src ++;
else
{
nums[dst ++] = nums[src ++];
}
}
return dst;
}
（2）比较含退格的字符串
解题思路：
（1）逆序遍历，从两个字符串的后面往前遍历；
（2）定义
skip表示当前待删除的字符的数量。每次我们遍历到一个字符，若为#则skip++；（3）到最后
skip为 0 的时候再将两个字符进行比较；
- 示例代码如下：
class Solution {
public:
bool backspaceCompare(string S, string T) {
int i = S.length() - 1, j = T.length() - 1;
int skipS = 0, skipT = 0;
while (i >= 0 || j >= 0) {
while (i >= 0) {
if (S[i] == '#') {
skipS++, i--;
} else if (skipS > 0) {
skipS--, i--;
} else {
break;
}
}
while (j >= 0) {
if (T[j] == '#') {
skipT++, j--;
} else if (skipT > 0) {
skipT--, j--;
} else {
break;
}
}
if (i >= 0 && j >= 0) {
if (S[i] != T[j]) {
return false;
}
} else {
if (i >= 0 || j >= 0) {
return false;
}
}
i--, j--;
}
return true;
}
};
（3）有序数组的平方
思路分析：
（1）观察题目，是递增的序列，因此只需要用两个指针指向起始位置和终止位置即可
class Solution {
public:
vector<int> sortedSquares(vector<int>& A) {
int k = A.size() - 1;
vector<int> result(A.size(), 0);
for (int i = 0, j = A.size() - 1; i <= j;) { // 注意这里要i <= j，因为最后要处理两个元素
if (A[i] * A[i] < A[j] * A[j]) {
result[k--] = A[j] * A[j];
j--;
}
else {
result[k--] = A[i] * A[i];
i++;
}
}
return result;
}
};
（3）长度最小的子数组
- 双指针的应用：滑动窗口
用一个 for 循环，是表示滑动窗口的
终止位置；
- 示例代码如下：
int minSubArrayLen(int target, int* nums, int numsSize){
// 枚举滑动窗口的右边界
int sum = 0, j = 0, ans = INT_MAX;
for (int i = 0; i < numsSize; i ++)
{
sum += nums[i];
while (sum >= target)
{
int len = i - j + 1;
if (len < ans)
ans = len;
sum -= nums[j];
j ++; // 不断移动左边界
}
}
if (ans == INT_MAX)
return 0;
else
return ans;
}
（4）水果成篮
解题思路：
示例代码如下：
class Solution {
public:
int totalFruit(vector<int>& fruits) {
int left = 0, n = fruits.size();
unordered_map<int, int> cnt; // 建立窗口中的每种数的 键值对
int ans = 0;
for (int right = 0; right < n; right ++ )
{
cnt[fruits[right]] ++;
while (cnt.size() > 2) // 超过两个键值对的情况
{
cnt[fruits[left]] --;
if (cnt[fruits[left]] == 0)
{
cnt.erase(cnt.find(fruits[left])); // 注意此处代码！！！
}
left ++;
}
ans = max(right - left + 1, ans);
}
return ans;
}
};
三、模拟题
- 注意事项：
（1）
坚持循环不变量的原则，坚持了每条边左闭右开的原则；（2）按照固定规则遍历，填充上行从左到右，填充右列从上到下，填充下行从右到左，填充左列从下到上；
（3）由外向内一圈一圈这么画下去；
（1）螺旋矩阵 II
- 示例代码如下：
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
int startx = 0, starty = 0;
int T = n / 2; // 循环的圈数
int i, j;
int offset = 1; // 偏移量
int count = 1;
// 遵循 循环不变量 左闭右开的原则 如：[1,3),[3,5),[5,7)就是左闭右开的原则
while (T --)
{
// 先填充 北部的边
for (i = starty; i < n - offset; i ++)
res[startx][i] = count ++;
// 再填充 东部的边
for (j = startx; j < n - offset; j ++)
res[j][i] = count ++;
// 再填充 南部的边
for (;i > starty; i --)
res[j][i] = count ++;
// 再填充 西部的边
for (;j > startx; j --)
res[j][i] = count ++;
startx ++;
starty ++;
offset ++;
}
if (n % 2 != 0)
res[n / 2][n / 2] = count;
return res;
}
};
（2）螺旋矩阵
解题思路如下：
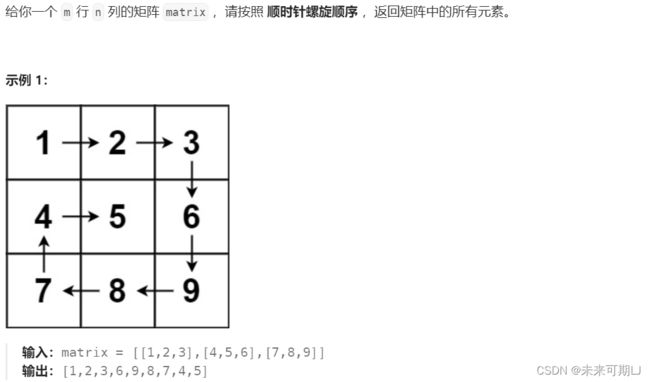
- 示例代码如下：
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int n = matrix.size(), m = matrix[0].size(); // n: 行数；m：列数
vector<int> ans;
int up = 0, down = n - 1, left = 0, right = m - 1;
while (true)
{
// 先遍历北部
for (int i = left; i <= right; i ++)
ans.push_back(matrix[up][i]);
if (++ up > down) break;
// 再遍历东部
for (int i = up; i <= down; i ++)
ans.push_back(matrix[i][right]);
if (-- right < left) break;
// 遍历南部
for (int i = right; i >= left; i --)
ans.push_back(matrix[down][i]);
if (-- down < up) break;
// 遍历西部
for (int i = down; i >= up; i --)
ans.push_back(matrix[i][left]);
if (++ left > right) break;
}
return ans;
}
};
四、总结
耗时三天，终于拿下数组篇，加油，加油，加油，冲冲冲！！！