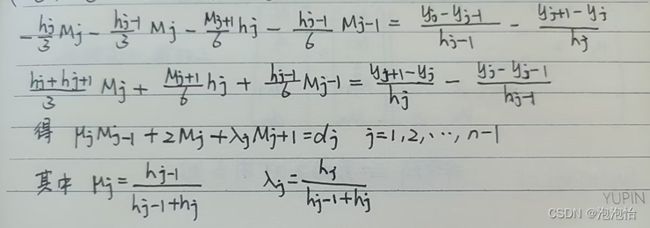三次样条插值证明过程及代码实现

一、什么是插值？

已知部分离散的数据点，但不知道满足这些数据点的函数表达式，插值、拟合都是寻找对应点的函数表达式。区别在于，插值函数是通过这些点，而拟合是要求形似而不要求穿过已知数据点。

二、常见的插值方法 

1.拉格朗日插值

2.埃尔米特插值（插值多项式在插值节点上函数值相等，再节点上的导数值也相等）

3.分段低次插值：

它的提出是由于高次插值的病态性质：从拉格朗日插值的余项可以看出。当节点增加且l(x)的次数n增加时，l(x)逼近f(x)的精度就越好，但实际并非如此。当n趋于无穷大的时候，l(n)不一定收敛到f(x).并且函数曲线会出现剧烈的振荡，即龙格现象。

for i=3:2:11
x=linspace(-1,1,i);
y=1./(1+25*x.^2);
p=polyfit(x,y,i-1);
xx=-1:0.01:1;
yy=polyval(p,xx);
plot(xx,yy,'b');
hold on;
grid on;
end;
plot(x,1./(1+25*x.^2),'r');

结果： 

4. 三次样条插值：

 对于分段低次插值函数都有一致收敛性，但光滑度较差，对于像高速飞机的机翼形状、船体放样灯型值线往往需要有二阶光滑度。三次样条插值函数就是把已知数据分割成若干个小区间，在每个小区间上都是三次多项式，并且一阶导数连续，二阶导数连续，函数值也连续。

疑问?为什么会有边界条件？（我们这篇博文写的是确定n+1个点的三次样条插值多项式）

由于三次样条插值函数在每个小区间上是三次多项式，所以在每个小区间上有四个待定参数，n+1个节点n个区间，所以有4n个参数，而根据插值条件和一次连续可微所含的条件有4n-2个条件，因此还要加两个两个条件，即边界条件。       

三、详细推导过程

（一）   设出S(x)函数

（二） S(x)的二阶导连续

 （三）边界条件

 （四）由于S（x）的二阶导数为线性函数形式简单。可以设出二阶导数的表达式，然后再积分两次就可以得到S（x）的表达式再求出参数

 两次积分最后整理：

 再利用一阶导数连续求M：

 整理可得

 

上面给出了含有n+1个参数 的n-1个方程，下面利用边界条件再给出2个方程。

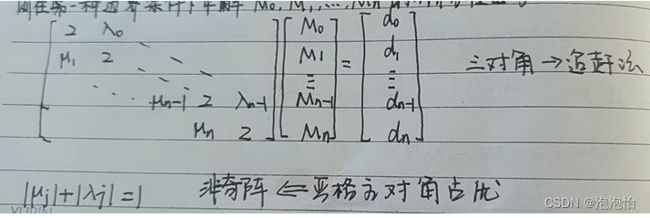
 第一种边界条件下可解出求解M的n阶方程组为: 

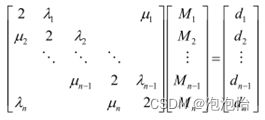
第二种边界条件下可解出求解M的n-1阶方程组为

第三种边界条件：

 求解利用追赶法。

四、python代码：

import matplotlib.pyplot as plt
import pandas as pd
from scipy import interpolat
data = pd.read_excel('C:/Users/bwy/Desktop/三样条.xlsx')
x = data['x']  # 取第一列数据
y = data['value']  # 取第二列数据
# 进行样条插值
tck = interpolate.splrep(x,y)
xx = np.linspace(min(x),max(x),100)
yy = interpolate.splev(xx,tck,der=0)
print(yy)
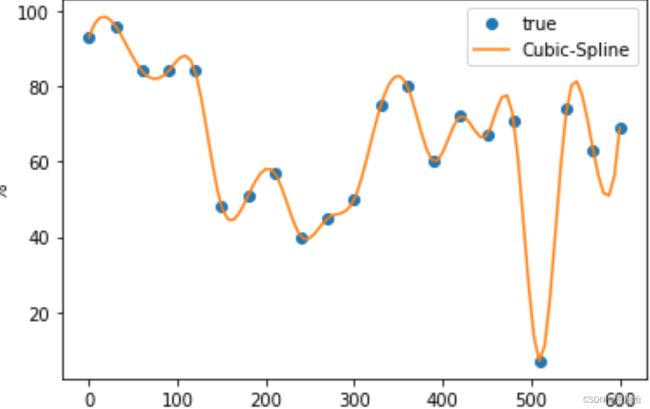
plt.plot(x,y,'o',xx,yy)
plt.show()

结果：