开源代码 | FMCW-MIMO雷达仿真MATLAB

本文编辑：调皮哥的小助理

本程序来源：https://github.com/ekurtgl/FMCW-MIMO-Radar-Simulation，作者是阿拉巴马大学博士生艾库特格尔，研究方向主要是雷达信号处理人类活动识别以及雷达数据的机器学习应用，这份比较新的开源雷达仿真代码，值得大家学习。

下面主要分析代码的主要内容，方便大家解读。

程序目录如下：

图片

FMCW_simulation.m是创建点目标并估计其范围、速度和角度信息的主脚本，首先研究这个脚本程序。

一、雷达参数

雷达参数的设置，属于是老生常谈了，之前的文章已经谈到很多了，不再详细重复论述。不过在本程序中，需要注意PRI默认为等于Chirp持续时长，实际上还要考虑空闲时间。这里的带宽指的是有效带宽，而不是发射信号带宽。程序中一共设置了10帧、1T8R，这些参数都是可以修改的。

```c
> %% Radar parameters
c = physconst('LightSpeed'); %speed of light
BW = 150e6; %bandwidth 有效
fc = 77e9; % carrier frequency
numADC = 256; % # of adc samples
numChirps = 256; % # of chirps per frame
numCPI = 10;
T = 10e-6; % PRI，默认不存在空闲时间
PRF = 1/T;
Fs = numADC/T; % sampling frequency
dt = 1/Fs; % sampling interval
slope = BW/T;
lambda = c/fc;
N = numChirps*numADC*numCPI; % total # of adc samples
t = linspace(0,T*numChirps*numCPI,N); % time axis, one frame 等间隔时间/点数
t_onePulse = 0:dt:dt*numADC-dt; %单chirp时间
numTX = 1;
numRX = 8; %等效后
Vmax = lambda/(T*4); % Max Unamb velocity m/s
DFmax = 1/2*PRF; % = Vmax/(c/fc/2); % Max Unamb Dopp Freq
dR = c/(2*BW); % range resol
Rmax = Fs*c/(2*slope); % TI's MIMO Radar doc
Rmax2 = c/2/PRF; % lecture 2.3
dV = lambda/(2*numChirps*T); % velocity resol, lambda/(2*framePeriod)
d_rx = lambda/2; % dist. between rxs
d_tx = 4*d_rx; % dist. between txs
N_Dopp = numChirps; % length of doppler FFT
N_range = numADC; % length of range FFT
N_azimuth = numTX*numRX;
R = 0:dR:Rmax-dR; % range axis
V = linspace(-Vmax, Vmax, numChirps); % Velocity axis
ang_ax = -90:90; % angle axis

二、目标参数

这里的目标参数就采用极坐标系转直角坐标系，然后分别用X方向的速度和Y方向上的速度乘上时间，带入后续的计算。

> %% 目标参数
r1_radial = 50; 
v1_radial = 10; % velocity 1
tar1_angle = -10;
r1_y = cosd(tar1_angle)*r1_radial;
r1_x = sind(tar1_angle)*r1_radial;
v1_y = cosd(tar1_angle)*v1_radial;
v1_x = sind(tar1_angle)*v1_radial;
r1 = [r1_x r1_y 0];
r2_radial = 100;
v2_radial = -15; % velocity 2
tar2_angle = 10;
r2_y = cosd(tar2_angle)*r2_radial;
r2_x = sind(tar2_angle)*r2_radial;
v2_y = cosd(tar2_angle)*v2_radial;
v2_x = sind(tar2_angle)*v2_radial;
r2 = [r2_x r2_y 0];
%发射天线位置
tx_loc = cell(1,numTX);
for i = 1:numTX
   tx_loc{i} = [(i-1)*d_tx 0 0];
   scatter3(tx_loc{i}(1),tx_loc{i}(2),tx_loc{i}(3),'b','filled')
   hold on
end
% 接收天线位置
rx_loc = cell(1,numRX);
for i = 1:numRX
   rx_loc{i} = [tx_loc{numTX}(1)+d_tx+(i-1)*d_rx 0 0];
   scatter3(rx_loc{i}(1),rx_loc{i}(2),rx_loc{i}(3),'r','filled')
end
tar1_loc = zeros(length(t),3);
tar1_loc(:,1) = r1(1) + v1_x*t;
tar1_loc(:,2) = r1(2) + v1_y*t;
tar2_loc = zeros(length(t),3);
tar2_loc(:,1) = r2(1) + v2_x*t;
tar2_loc(:,2) = r2(2) + v2_y*t;

同时，这里还绘制了发射天线和接收天线的位置图，蓝色为发射天线位置，红色为接收天线位置。这个位置信息后面会用于计算目标的时间延迟。

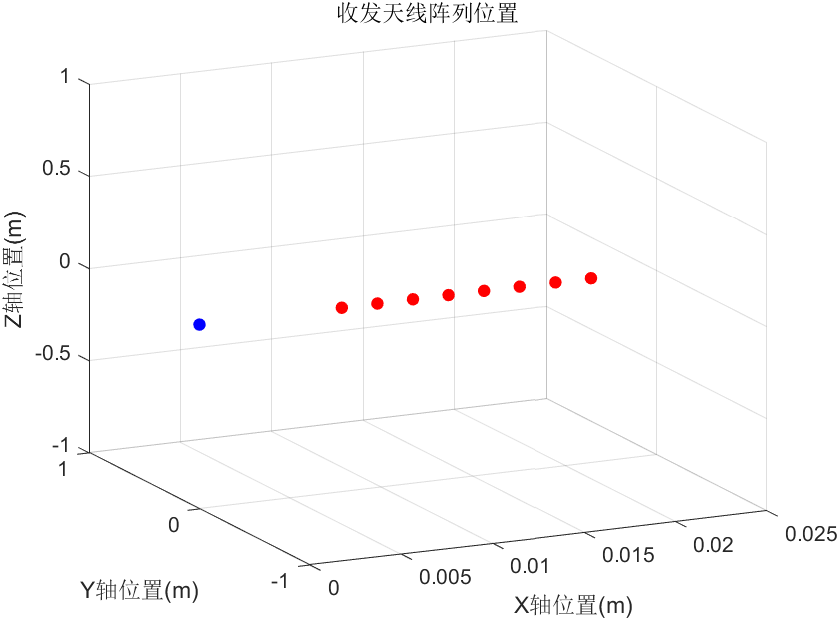
三、发射信号建模

利用收发天线的位置以及目标参数中雷达的位置信息，先求目标到雷达的2-范数（也就是空间中两点的直线距离），然后转化为目标的延迟时间τ，如此以来得到的信号模型精度更高！这样的方法，与往常采用的不同，可以说以前的方法有点粗暴，虽同为远场条件，但是没有考虑阵列的位置对信号的影响！

> %% TX siganl
delays_tar1 = cell(numTX,numRX);
delays_tar2 = cell(numTX,numRX);
r1_at_t = cell(numTX,numRX);
r2_at_t = cell(numTX,numRX);
tar1_angles = cell(numTX,numRX);
tar2_angles = cell(numTX,numRX);
tar1_velocities = cell(numTX,numRX);
tar2_velocities = cell(numTX,numRX);
for i = 1:numTX
    for j = 1:numRX
        delays_tar1{i,j} = (vecnorm(tar1_loc-repmat(rx_loc{j},N,1),2,2)+vecnorm(tar1_loc-repmat(tx_loc{i},N,1),2,2))/c; 
        delays_tar2{i,j} = (vecnorm(tar2_loc-repmat(rx_loc{j},N,1),2,2)+vecnorm(tar2_loc-repmat(tx_loc{i},N,1),2,2))/c;
    end
end

四、接收信号模型

这里，接收信号没有采用发射与接收混频的形式，而是相位直接做差，分别计算两个目标的中频信号相加，此法等效为混频。其中@（tx，fx）相当于传参函数，用于后面的等式计算。

中频信号除了目标的距离表征的频率之外，还有目标运动速度引起的多普勒频移，是两部分的叠加。

> %% Complex signal
phase = @(tx,fx) 2*pi*(fx.*tx+slope/2*tx.^2); % transmitted
phase2 = @(tx,fx,r,v) 2*pi*(2*fx*r/c+tx.*(2*fx*v/c + 2*slope*r/c)); % downconverted
% f_oneChirp =  slope*t(1:sum(t<=T));
% f_t = repmat(f_oneChirp,1,numChirps*numCPI)-(BW/2); % transmit freq
% f_t = BW/2*sawtooth(t/T*2*pi); 
fr1 = 2*r1(2)*slope/c; 
fr2 = 2*r2(2)*slope/c;
fd1 = 2*v1_radial*fc/c; % doppler freq
fd2 = 2*v2_radial*fc/c;
f_if1 = fr1 + fd1;      % beat or IF freq
f_if2 = fr2 + fd2;
% mixed1 = cell(numTX,numRX);
% mixed2 = cell(numTX,numRX);
mixed = cell(numTX,numRX);
for i = 1:numTX
    for j = 1:numRX
        disp(['Processing Channel: ' num2str(j) '/' num2str(numRX)]);
        for k = 1:numChirps*numCPI
            phase_t = phase(t_onePulse,fc);
            phase_1 = phase(t_onePulse-delays_tar1{i,j}(k*numADC),fc); % received
            phase_2 = phase(t_onePulse-delays_tar2{i,j}(k*numADC),fc);
            signal_t((k-1)*numADC+1:k*numADC) = exp(1j*phase_t);
            signal_1((k-1)*numADC+1:k*numADC) = exp(1j*(phase_t - phase_1));
            signal_2((k-1)*numADC+1:k*numADC) = exp(1j*(phase_t - phase_2));
        end
        mixed{i,j} = signal_1 + signal_2;
    end
end

绘制出的局部结果如下，若要观察全部的信号，则需要修改X轴的范围限制。

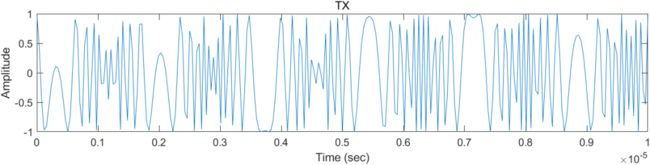
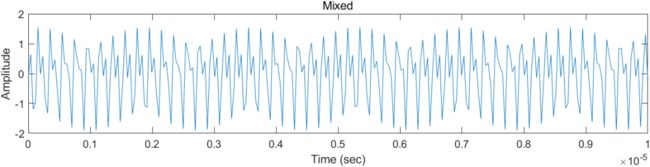
五、2D-FFT

上面我一句雷达信号处理原理方面的内容都没有提及，主要是这些基础的内容，我默认各位都已经清楚了。如果不清楚，那就先去搞清楚再回头来看（调皮连续波公众号里有），不然可能会遇到理解困难。

首先生成一个三维的DataCube，然后每个CPI做一次2D-FFT就OK了，没啥难度，顶多就是数据组成或者格式，理解起来有些麻烦，不过这都不是核心难题。

> RDC = reshape(cat(3,mixed{:}),numADC,numChirps*numCPI,numRX*numTX); % radar data cube
RDMs = zeros(numADC,numChirps,numTX*numRX,numCPI);
for i = 1:numCPI
    RD_frame = RDC(:,(i-1)*numChirps+1:i*numChirps,:);
    RDMs(:,:,:,i) = fftshift(fft2(RD_frame,N_range,N_Dopp),2);
end
figure
imagesc(V,R,20*log10(abs(RDMs(:,:,1,1))/max(max(abs(RDMs(:,:,1,1))))));
colormap(jet(256))
% set(gca,'YDir','normal')
clim = get(gca,'clim');
caxis([clim(1)/2 0])
xlabel('Velocity (m/s)');
ylabel('Range (m)');

处理结果如下：

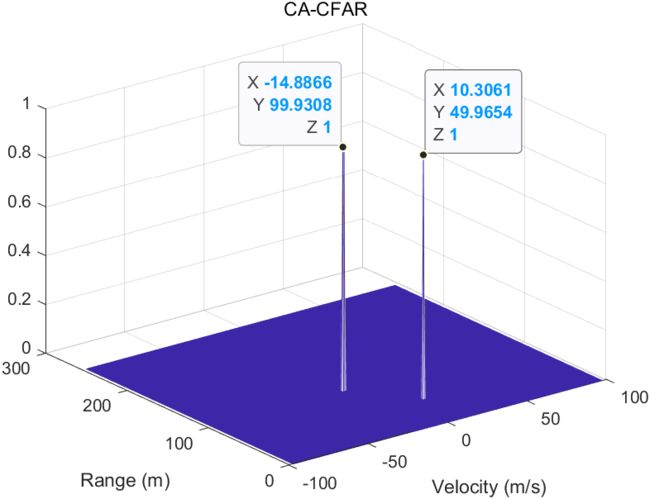
化成三维的可以标注数据，方便查看解算的结果以及误差，可见距离和速度都基本吻合，存在些许误差。

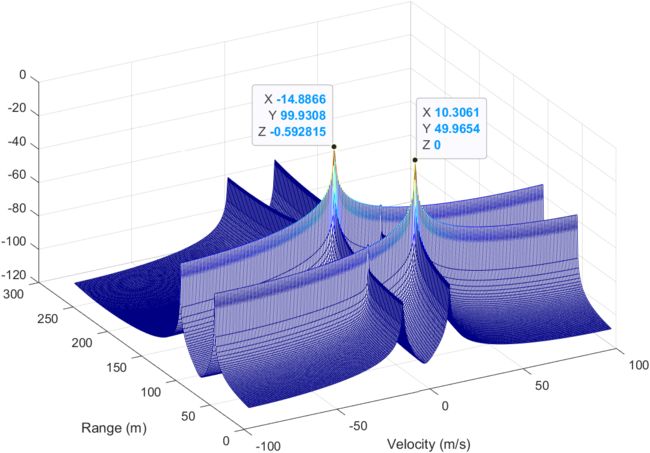
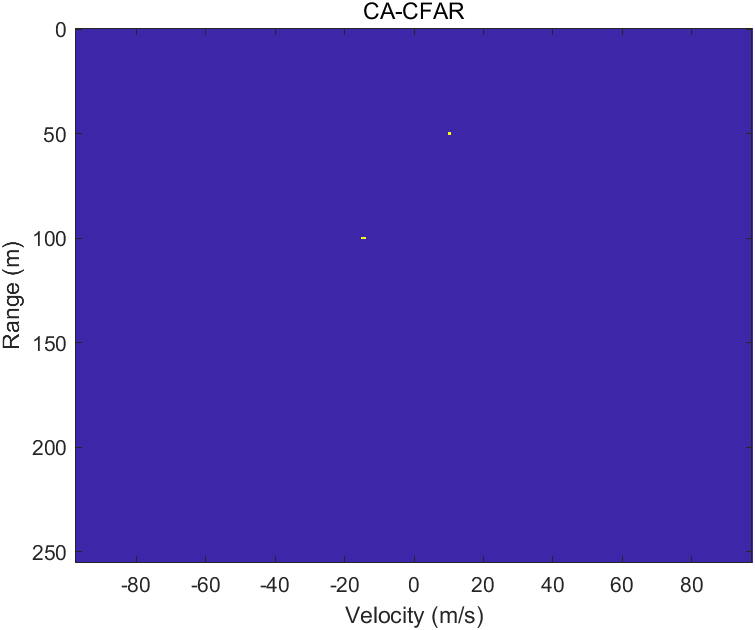
六、CA-CFAR

代码一读就懂，老生常谈的东西了，没啥可讲的。

> numGuard = 2; % # of guard cells
numTrain = numGuard*2; % # of training cells
P_fa = 1e-5; % desired false alarm rate 
SNR_OFFSET = -5; % dB
RDM_dB = 10*log10(abs(RDMs(:,:,1,1))/max(max(abs(RDMs(:,:,1,1)))));
[RDM_mask, cfar_ranges, cfar_dopps, K] = ca_cfar(RDM_dB, numGuard, numTrain, P_fa, SNR_OFFSET);
figure
h=imagesc(V,R,RDM_mask);
xlabel('Velocity (m/s)')
ylabel('Range (m)')
title('CA-CFAR')

处理结果：

七、角度估计

（一）3D-FFT

常规操作，基本内容，没啥难度。

```c
> rangeFFT = fft(RDC(:,1:numChirps,:),N_range);
angleFFT = fftshift(fft(rangeFFT,length(ang_ax),3),3);
range_az = squeeze(sum(angleFFT,2)); % range-azimuth map
figure
colormap(jet)
% imagesc(ang_ax,R,20*log10(abs(range_az)./max(abs(range_az(:))))); 
mesh(ang_ax,R,20*log10(abs(range_az)./max(abs(range_az(:))))); 
xlabel('Azimuth Angle')
ylabel('Range (m)')
title('FFT Range-Angle Map')
set(gca,'clim', [-35, 0])
doas = zeros(K,181); % direction of arrivals
figure
hold on; grid on;
for i = 1:K
    doas(i,:) = fftshift(fft(rangeFFT(cfar_ranges(i),cfar_dopps(i),:),181));
    plot(ang_ax,10*log10(abs(doas(i,:))))
end
xlabel('Azimuth Angle')
ylabel('dB')

运行结果如下：


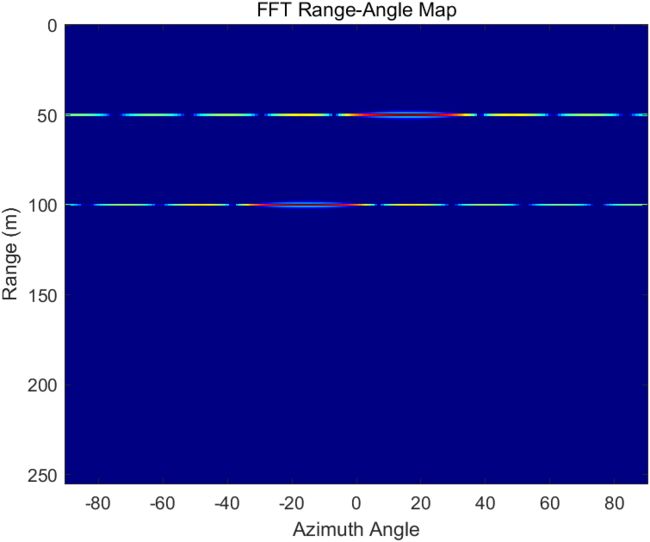
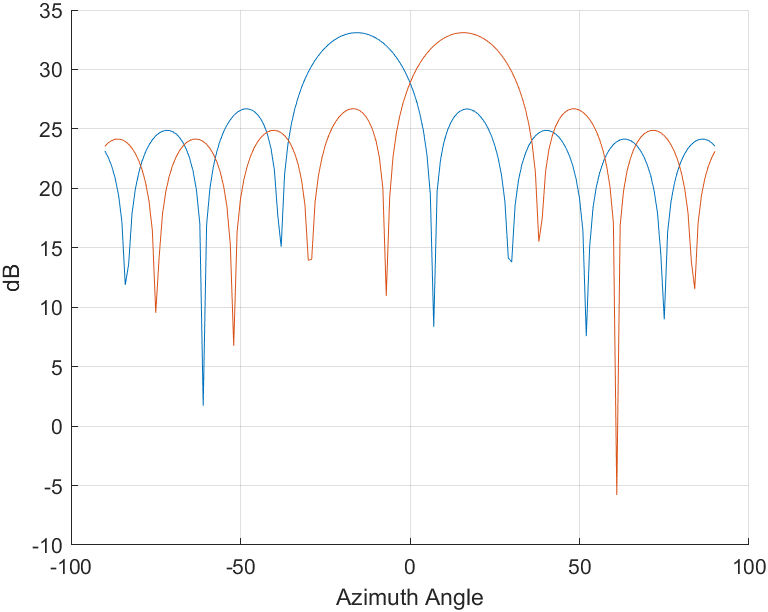
可见，角度并不是很准确，读者可以验证，目标角度越偏离发现，误差越大。这其实与雷达的角度分辨率有关，用下文的超分辨算法可以改善。

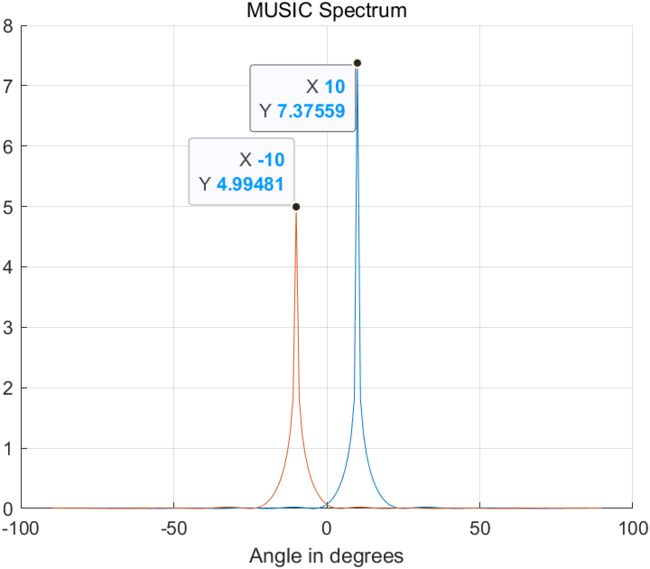
（二）MUSIC算法

有读者常问，说MUSIC在网上找到的代码都是仿真的，很少看到有对实际目标的数据进行处理的，这不就来了嘛。不过，说到底还是见的太少。

MUSIC算法原理默认都清楚，不清楚的自己查阅相关资料。

> d = 0.5;
M = numCPI; % # of snapshots
for k=1:length(ang_ax)
        a1(:,k)=exp(-1i*2*pi*(d*(0:numTX*numRX-1)'*sin(ang_ax(k).'*pi/180)));
end
for i = 1:K
    Rxx = zeros(numTX*numRX,numTX*numRX);
    for m = 1:M
       A = squeeze(RDMs(cfar_ranges(i),cfar_dopps(i),:,m));
       Rxx = Rxx + 1/M * (A*A');
    end
    [Q,D] = eig(Rxx); % Q: eigenvectors (columns), D: eigenvalues
    [D, I] = sort(diag(D),'descend');
    Q = Q(:,I); % Sort the eigenvectors to put signal eigenvectors first
    Qs = Q(:,1); % Get the signal eigenvectors
    Qn = Q(:,2:end); % Get the noise eigenvectors
    for k=1:length(ang_ax)
        music_spectrum(i,k)=(a1(:,k)'*a1(:,k))/(a1(:,k)'*(Qn*Qn')*a1(:,k));
    end
end

运行结果漂亮的很，不要管幅度差异，幅度不代表功率。

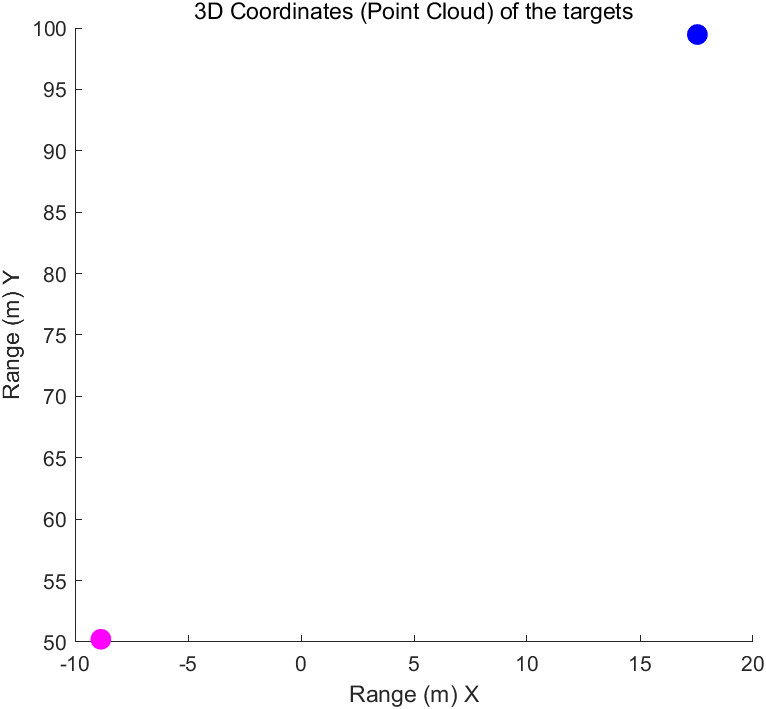
（三）点云生成

坐标转换即可，若想要点云数量更多，可以降低CFAR门限，放更多的目标点进来。

> [~, I] = max(music_spectrum(2,:));
angle1 = ang_ax(I);
[~, I] = max(music_spectrum(1,:));
angle2 = ang_ax(I);
coor1 = [cfar_ranges(2)*sind(angle1) cfar_ranges(2)*cosd(angle1) 0];
coor2 = [cfar_ranges(1)*sind(angle2) cfar_ranges(1)*cosd(angle2) 0];
figure
hold on;
title('3D Coordinates (Point Cloud) of the targets')
scatter3(coor1(1),coor1(2),coor1(3),100,'m','filled','linewidth',9)
scatter3(coor2(1),coor2(2),coor2(3),100,'b','filled','linewidth',9)
xlabel('Range (m) X')
ylabel('Range (m) Y')
zlabel('Range (m) Z')

处理结果：

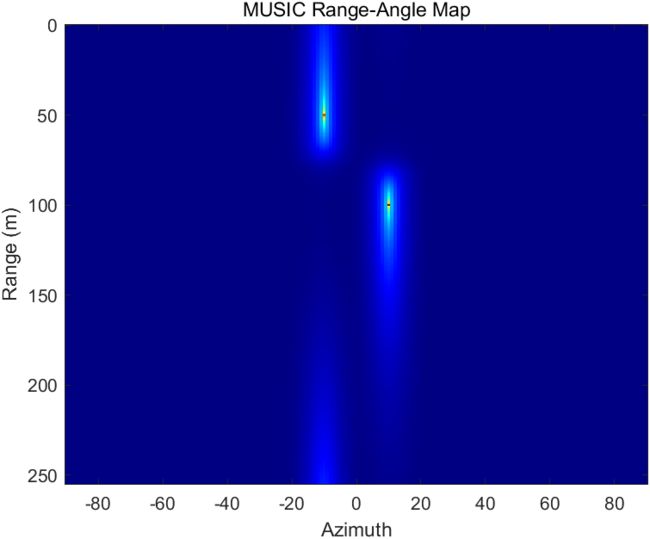
（四）MUSIC 距离-AOA谱

算法没变，绘图方式不同而已。

> rangeFFT = fft(RDC);
for i = 1:N_range
    Rxx = zeros(numTX*numRX,numTX*numRX);
    for m = 1:M
       A = squeeze(sum(rangeFFT(i,(m-1)*numChirps+1:m*numChirps,:),2));
       Rxx = Rxx + 1/M * (A*A');
    end
%     Rxx = Rxx + sqrt(noise_pow/2)*(randn(size(Rxx))+1j*randn(size(Rxx)));
    [Q,D] = eig(Rxx); % Q: eigenvectors (columns), D: eigenvalues
    [D, I] = sort(diag(D),'descend');
    Q = Q(:,I); % Sort the eigenvectors to put signal eigenvectors first
    Qs = Q(:,1); % Get the signal eigenvectors
    Qn = Q(:,2:end); % Get the noise eigenvectors
    for k=1:length(ang_ax)
        music_spectrum2(k)=(a1(:,k)'*a1(:,k))/(a1(:,k)'*(Qn*Qn')*a1(:,k));
    end
    range_az_music(i,:) = music_spectrum2;
end
figure
colormap(jet)
imagesc(ang_ax,R,20*log10(abs(range_az_music)./max(abs(range_az_music(:))))); 
xlabel('Azimuth')
ylabel('Range (m)')
title('MUSIC Range-Angle Map')
clim = get(gca,'clim');

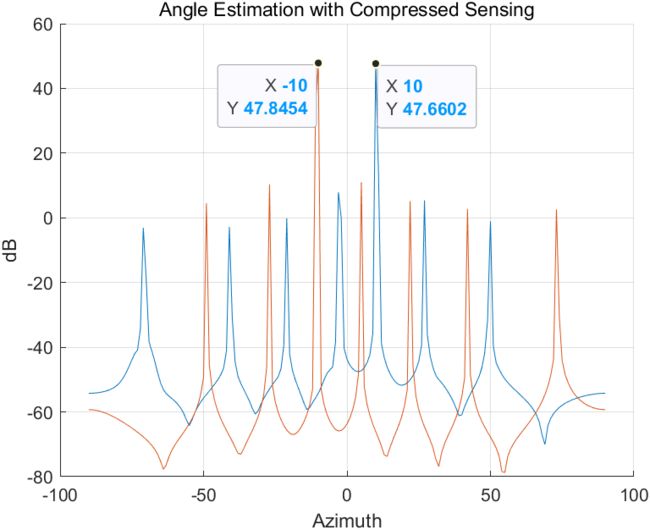
（五）压缩感知

原理捎带复杂，但主要还是一个凸优化问题。

> figure
hold on; grid on;
title('Angle Estimation with Compressed Sensing')
xlabel('Azimuth')
ylabel('dB')
for i = 1:K
    A = squeeze(RDMs(cfar_ranges(i),cfar_dopps(i),:,1));
    cvx_begin
        variable s(numTheta) complex; %alphax(numTheta,1) phix(numTX*numRX,numTheta)...
            %cap_theta(numTX*numRX,numTheta) %B(numTX*numRX,numTheta)%psix(numTheta,numTheta) %A(numRX*numTX,1) % A is the initial measurement
    %     cap_theta == phix * psix;
    %     minimize(norm(alphax,1))
    %     pow_p(norm(A-cap_theta*alphax,2),2) <= 1;
    %     norm(A-cap_theta*alphax,2) <= 1;
    %     minimize(norm(A-cap_theta*alphax,1))
        minimize(norm(s,1))
        norm(A-B*s,2) <= 1;
    cvx_end
    cvx_status
    cvx_optval
    plot(ang_ax,10*log10(abs(s)))
end

第一个脚本的内容就说完了，下面是第二个脚本。

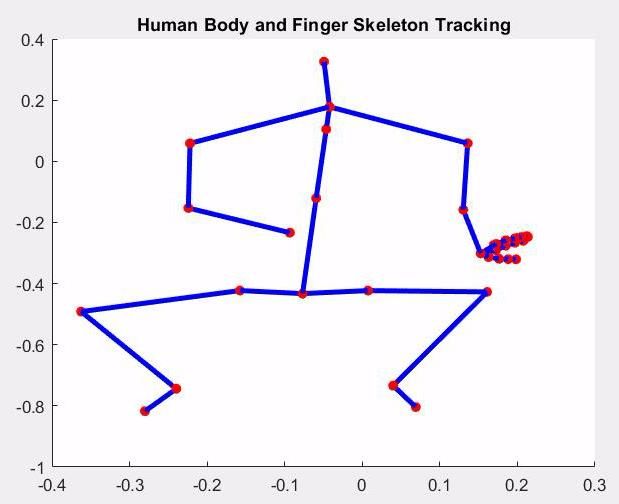
FMCW_sim_v2.m是读取 Kinect v2 设备捕获的人体骨骼关节三维坐标，提取原始雷达数据立方体 （RDC） 并播放距离多普勒图、输出微多普勒频谱图的主脚本。

Kinect v2里人体骨骼结构如下：

距离多普勒图：

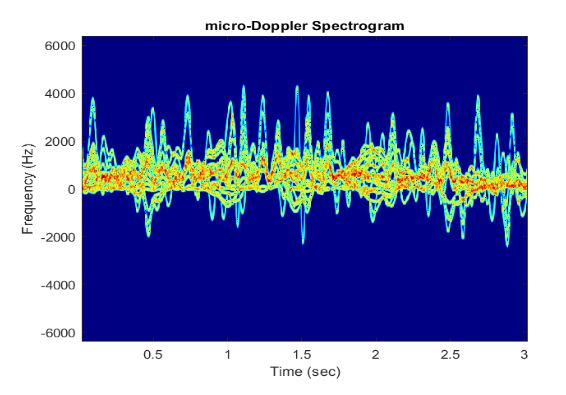
微多普勒频谱图：

> rBin = 1:256;
nfft = 2^12;window = 256;noverlap = 200;shift = window - noverlap;
sx = myspecgramnew(sum(RDC(rBin,:,:)),window,nfft,shift); % mti filter and IQ correction
sx2 = abs(flipud(fftshift(sx,1)));
timeAxis = [1:numCPI]*frameDuration; % Time
freqAxis = linspace(-PRF/2,PRF/2,nfft); % Frequency Axis
fig = figure('visible','on');
colormap(jet(256));
% set(gca,'units','normalized','outerposition',[0,0,1,1]);
doppSignMTI = imagesc(timeAxis,[-PRF/2 PRF/2],20*log10(abs(sx2/max(sx2(:)))));
%     axis xy
%     set(gca,'FontSize',10)
title('micro-Doppler Spectrogram');
%     title(fOut(end-22:end-4))
xlabel('Time (sec)');
ylabel('Frequency (Hz)');
caxis([-45 0]) % 40
set(gca, 'YDir','normal')
set(gcf,'color','w');

对该开源仿真代码感兴趣的读者，可以访问链接：https://github.com/ekurtgl/FMCW-MIMO-Radar-Simulation。

修改后的代码放到云盘了，修改的不多，如有需要，后台回复“2022”获得下载链接。

【本期结束】